| Дициплина | Математика (Алгебра) | Курс 2-семестр |
| Группа ЮК-2-19 | Группа ЮК-3-19 | Группа ЮК-4-19 |
| Дата “___”______2020г. | Дата “___”______2020г. | Дата “___”______2020г. |
Тема: Корень n-й степени и его свойства (4ч)
Цель занятия:
Образовательные:
-дать определение корня n-ой степени;
-научить применять свойства корня n-ой степени при решении задач
Развивающие:
-развитие внимания, познавательной активности, памяти, мышления;
-развивать навыки самостоятельного применения знаний в знакомой и измененной ситуации;
Воспитательные:
-воспитание познавательного интереса к дисциплине.
Ход занятия
Сегодня на уроке мы познакомимся со следующими понятиями: корень n-ой степени, арифметический корень n-ой степени из числа, с решениями уравнений вида хn=a.
Устная работа. Актуализация прежних знаний.
Выполнение заданий на вычисление квадрата числа.
Вычислите:
72; 0,52; 1,62; (-17)2; 202.
Задание. Вместо x поставьте числа так, чтобы равенства были верными:
| 3-класс | 2х=10 х=5 |
| 6-класс | 10х=2 х=2/10 х=1/5 |
| 8-класс | х2=25 х2=0,25 х2=100 х=5 х=-5 |
|
| х3=8 х3=8 х=2 х=-2 23=8 |
| 
| х3=3 х= 3√3 3√3 |
|  √ - радикал n - показатель корня а - подкоренное число (выражение)
| х7=2 х=7√2 |
Определение. Квадратным корнем из числа а называют число, квадрат которого равен а.
Аналогично определим корень n-ой степени. Корнем n-ой степени из числа а называется такое число, n-я степень которого равна а.
Примеры:
Корень третьей степени из числа 27 равен 3, т.к. 33=27.
Корень шестой степени из числа 64 равен 2 и (-2), т.к. 26=64 и (-2)6=64.
Согласно данному определению, корень n-ой степени из числа а – это решение уравнения хn=а. Число корней данного уравнения зависит от n и а.
Определение корня n-ой степени.
Радикалом (или знаком корня) называют знак  , применяемый для обозначения операции извлечения корня n-ой степени из некоторого числа, корень n-ой степени из числа a обозначается
, применяемый для обозначения операции извлечения корня n-ой степени из некоторого числа, корень n-ой степени из числа a обозначается  . При n
. При n 2 показатель корня опускают и пишут
2 показатель корня опускают и пишут  вместо
вместо  . Корень второй степени обычно называют квадратным корнем, а корень третьей степени – кубическим корнем. При извлечении корня четной степени из неотрицательного числа а запись
. Корень второй степени обычно называют квадратным корнем, а корень третьей степени – кубическим корнем. При извлечении корня четной степени из неотрицательного числа а запись  обозначает арифметический корень из числа а (т. е. такое неотрицательное число в, что
обозначает арифметический корень из числа а (т. е. такое неотрицательное число в, что  =а).
=а).
При четном n существует два корня n-ой степени из любого положительного числа а; корень n-ой степени из числа 0 равен нулю; корней четной степени из отрицательных чисел не существует.
При нечетных значениях n функция  возрастает на всей числовой прямой; её область значений – множество всех действительных чисел.
возрастает на всей числовой прямой; её область значений – множество всех действительных чисел.
Применяя теорему о корне, находим, что уравнение,  =а имеет один корень при любом а и, в частности, при а
=а имеет один корень при любом а и, в частности, при а 0. Этот корень для любого значения а (в том числе и а отрицательного) обозначают
0. Этот корень для любого значения а (в том числе и а отрицательного) обозначают  .
.
Итак, при нечетном n существует корень n-ой степени из любого числа а, и при том только один.
Для корней нечетной степени справедливо равенство:  =-
=- .
.
Степенью числа а 0 с рациональным показателем r=
0 с рациональным показателем r=  , где 𝑚- целое число, а n - натуральное (n
, где 𝑚- целое число, а n - натуральное (n ), называется число
), называется число  .
.
Разминка: Устный счет. Задаваемые вопросы студентам:
Вычислить:
23
32
33
42

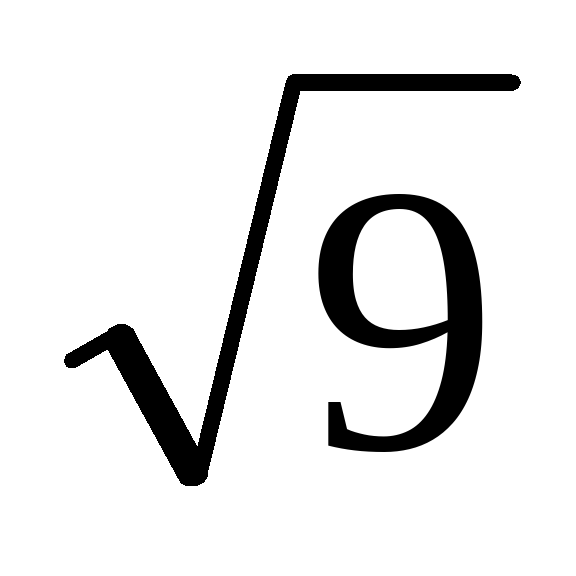


Степенью называется выражение вида:  , где:
, где:
 — основание степени;
— основание степени;
 — показатель степени.
— показатель степени.
Степень с натуральным показателем {1, 2, 3,...}
Определим понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
По определению:  .
.
Возвести число в квадрат — значит умножить его само на себя: 
Возвести число в куб — значит умножить его само на себя три раза:  .
.
Возвести число в натуральную степень  — значит умножить число само на себя
— значит умножить число само на себя  раз:
раз:
Степень с целым показателем {0, ±1, ±2,...}
Если показателем степени является целое положительное число:
 , n 0
, n 0
Возведение в нулевую степень:
 , a ≠ 0
, a ≠ 0
Если показателем степени является целое отрицательное число:
 , a ≠ 0
, a ≠ 0
Прим: выражение  не определено, в случае n ≤ 0. Если n 0, то
не определено, в случае n ≤ 0. Если n 0, то 
Пример 1.
Степень с рациональным показателем
Если:
a 0;
n — натуральное число;
m — целое число;
Тогда:
Свойства корня -ой степени.
Для любого натурального n, целого  и любых неотрицательных чисел а и в выполнено равенство:
и любых неотрицательных чисел а и в выполнено равенство:
1)  =
= 
2)  =
=  (причем в
(причем в
3)  =
=  (k
(k
4)  =
=  (k
(k
5)  = (
= ( (если k
(если k  0, то а
0, то а 0)
0)
ТАБЛИЦА СТЕПЕНЕЙ ЧИСЕЛ
Примеры
1) Найдите значения выражений:

 ;
;  ;
;  .
.
По определению степени с рациональным показателем и свойствами корней, имеем:

 =
=  = 2,
= 2,  =
=  = (
= ( =
=  = 27,
= 27,
 =
=  =(
=(  =
=  =
=  =
=  .
.
2) Сравним числа :  и
и  .
.
 =
=  =
=  =
=  ;
;
 =
=  =
=  =
=  ,
,
Т. к. 625 729, то
729, то 
 , значит
, значит  .
.
Работа по группам
| | Вариант I | Вариант II | Вариант I I I |
| Обязательный уровень (с выбором ответа) | А1. Вычислить:  1) 81; 2) 9; 3) 3; | А1. Вычислить:  1) 1; 2) 2; 3) 20; | А1. Вычислить: 1) 1; 2) 2; 3) 20; |
| А2. Вычислить: -2 1) -8; 2) 4; 3) -4; | А2. Вычислить  1) 100; 2) 10; 3) 1; | А2. Вычислить 1) 25; 2) 5; 3) 125; |
| А3. Вычислить:  1) 50; 2) 25; 3) 5; | А3. Вычислить: -6 1) - 24; 2) – 12; 3) 12; | А3. Вычислить: -2 1) - 24; 2) – 4; 3) 12; |
| А4. Решить уравнение: х6=64 1) 2; 2) -4; 4 3) -2; 2 | А4. Решить уравнение: х5=32 1) -2; 2) 2; 3) -2; 2 | А4. Решить уравнение: х5=243 1) -2; 2) 3; 3) -2; 2 |
| Обязательный уровень (указать ответ) | А5. Вычислить:  = = Ответ: | А5. Вычислить:  Ответ: | А5. Вычислить: Ответ: |
| А6. Преобразовать выражение:  = = Ответ: | А6. Преобразовать выражение:  Ответ: | А6. Преобразовать выражение: Ответ: |
Выполнение упражнений № 381- 392 б), г) № 393 – 407 б), г)
Итоги занятия
Домашнее задание № № 381- 392 а), в) № 393 – 407 а), в)
По учебнику «Алгебра и начала анализа» 10-11клас. А.Н. Колмогоров стр. 201-206


















