Вызовы времени обусловили необходимость разработки и внедрения новых стандартов школьного образования. В ФГОС ставится основная педагогическая задача – создание и организация условий, инициирующих детское действие; уже в основной школе должны подготовить учащихся к осознанному и основанному на предметных знаниях выбору будущей образовательной траектории.
Справедливости ради следует признать, что необходимости «инициировать детское действие» учащихся 4–7 классов особо и нет; активность на уроках у учащихся постепенно падает в старших классах из-за неправильной трактовки учителями вопроса «Как учить».
«Детское действие» сохранится, если подбором вопросов методики преподавания нового материала учителю удается от класса к классу постоянно активизировать мыслительную деятельность учащихся, сохранить и развивать их веру в свои способности.
В 21 веке дети активно используют возможности получения информации через интернет, телевидение, телефоны. Их природная приверженность к движению, активности отбивает желание усидчиво получать информацию через учебники; тем самым заметно уменьшается роль учебника в школьном процессе математического образования. Учебник, скорее, становится ориентацией для учеников и учащихся на уровень типовых примеров и заданий. Считаем, учитель на уроках мог бы переформулировать основные определения, понятия в терминах пошаговых действий и алгоритмов.
Другой вывод из новых стандартов: от порядка «действовать и думать» следует переходить к форме «думать и действовать». Именно такой подход за школьной партой позволит молодым людям «осознанно» принимать решения, «основанные на предметных знаниях» в самых различных жизненных ситуациях. Если в старой методике было уместно, решая уравнение 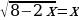 , возведением обеих частей в квадрат получить значения
, возведением обеих частей в квадрат получить значения 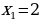 ,
, 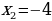 и, затем проверкой отбросить «лишний корень»
и, затем проверкой отбросить «лишний корень» 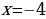 (принцип «действовать и думать»), то в духе новых стандартов сначала ученик, подумав, должен заметить, что
(принцип «действовать и думать»), то в духе новых стандартов сначала ученик, подумав, должен заметить, что 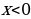 не может быть корнем уравнения и, следовательно, уравнение эквивалентно системе
не может быть корнем уравнения и, следовательно, уравнение эквивалентно системе 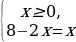 (принцип «думать и действовать»).
(принцип «думать и действовать»).
В рамках новых стандартов обучения отпадают такие понятия, как «лишний корень», «потеря корней»; с целью оптимизации обучения полезно в школьном курсе математики не вводить понятие «арифметический корень». Отдельные позиции этой работы ранее рассмотрены нами в 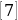 .
.
2. В основе изучения функции 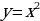 и
и 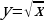 лежит функция
лежит функция 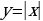 . Вот пример определения
. Вот пример определения 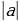 .
.
Чтобы понять, что такое 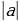 :
:
1) узнай знак 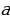 ;
;
2) если знак есть «+», то пиши 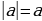 ; если же знак «
; если же знак «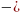 », то пиши
», то пиши 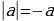 .
.
После следует выполнить два упражнения:
1) доказать, что 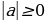 для любого
для любого 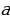 ;
;
2) для любых 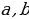 :
: 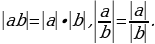
Учащимся следует внушить мысль, что, когда знак 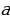 не знаем, можно перебрать всевозможные знаки (всего два!)
не знаем, можно перебрать всевозможные знаки (всего два!) 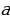 . Из второго упражнения получаются два следствия:
. Из второго упражнения получаются два следствия:
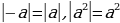 (1)
(1)
Мы рекомендуем доказать следующую теорему и в математическом кабинете иметь плакат с ее содержанием.
Теорема 1. Пусть 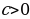 . Тогда
. Тогда
1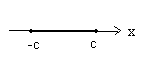 )
) 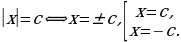
2) 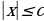 ⇔
⇔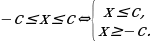
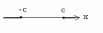
3) 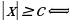
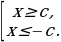
После доказательства следует отдельно рассмотреть случаи 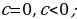 неравенства вида
неравенства вида 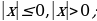 демонстрировать возможности использования теоремы на примерах решения неравенств вида:
демонстрировать возможности использования теоремы на примерах решения неравенств вида:
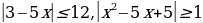 .
.
Возможности применения равенства (1):
1) Неравенства вида 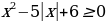 можно решить не только «снятием» модуля, но и его «одеванием»:
можно решить не только «снятием» модуля, но и его «одеванием»: 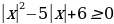 .
.
2) Уравнения вида 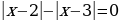 легче решить возведением обоих частей равенства
легче решить возведением обоих частей равенства 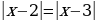 в квадрат:
в квадрат: 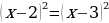 .
.
С целью активизирования мыслительной деятельности учащихся предложить им устные примеры на решение уравнений типа: 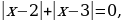
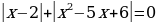 .
.
Другие примеры см. в [2], с.295-296, №№131(б, г),134.
3. Рассмотрим теперь вариант введения функции 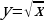 . Начинаем с определения. Чтобы вычислить
. Начинаем с определения. Чтобы вычислить 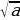 найди такое число
найди такое число 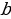 , что:
, что:
1) число 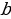 - неотрицательное,
- неотрицательное,
2)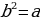 . Таким образом,
. Таким образом, 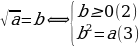
Следствия из определения.
10. Из (3) следует, что 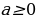 .
.
20. Из (2) следует, что 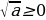 .
.
30. Из (3) следует, что 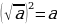 .
.
В 30 надо подчеркнуть, что 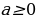 :
: 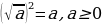 . Следовательно, у функции
. Следовательно, у функции 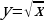 как область допустимых значений, так и область изменения есть множество всех неотрицательных чисел.
как область допустимых значений, так и область изменения есть множество всех неотрицательных чисел.
В КИМах ЕГЭ прошлых лет были предложены задания (в качестве С1) вида: 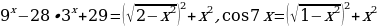 и учащиеся теряли 1 балл из двух, когда забывали о том, что
и учащиеся теряли 1 балл из двух, когда забывали о том, что 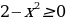 или
или 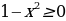 .
.
Полезно сравнить следствие 30 с равенствами (2) и предложить детям упростить выражение 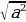 .
.
В контексте новых стандартов следует не просто дать детям формулу 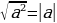 , а предложить с виду длинное правило.
, а предложить с виду длинное правило.
Чтобы упростить выражение 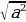 :
:
1) пытайся узнать знак 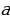 ;
;
2) узнал – радуйся:
если «+», то 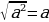 ,
,
если «–», то 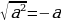 ;
;
3) не узнал – безрадостно пиши 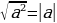 .
.
Приведем список рекомендуемых заданий:
А. Задание №47 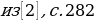
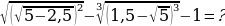 и др.
и др.
Б. Задания типа В из КИМов ЕГЭ прошлых лет:
C. Задания типа С1. Решить уравнения
а) 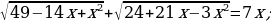
б) 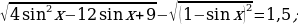
в) 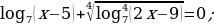
г) 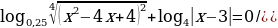
Указания. Уравнение а) равносильно системе 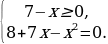
Уравнение г) равносильно уравнению 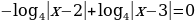
4. Следующее базовое понятие − правило возведения обеих частей в квадрат или извлечения корней четных порядков. Установить его можно, используя свойство монотонности функций 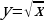 ;
; 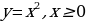 или непосредственной проверкой. Рекомендуем иметь в кабинете плакат.
или непосредственной проверкой. Рекомендуем иметь в кабинете плакат.
Правило 1.
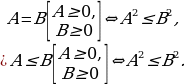
Правило 2.
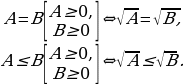
И предложить детям правило: если хочешь возводить обе части (уравнения или неравенства) в квадрат или извлечь квадратный корень, то сначала проверь условие неотрицательности двух частей. Если условие не выполняется, то нельзя возводить в квадрат, нельзя извлечь квадратный корень.
Указания. Если «условие» не выполняется, то либо надо обе части умножить на -1, либо применить правило сравнения знаков двух частей.
Считаем также необходимым иметь в кабинете таблицу типовых примеров и их решения.
Многоточия в таблице заменяют решения заданий. В первых трех столбцах «условие» выполняется. Например, 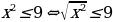 . Знак
. Знак 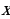 не знаем, следовательно,
не знаем, следовательно, 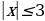 . Применяем 2) из теоремы 1:
. Применяем 2) из теоремы 1: 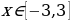 . Если
. Если 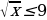 , то
, то 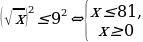
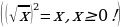 . Если же
. Если же 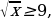 то
то 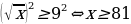 .
.
В трех последних столбцах «условие» не выполняется. Их разбираем сравнением знаков двух частей, причем во второй строке надо помнить об О.Д.З. Например
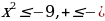
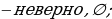
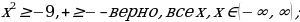
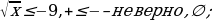
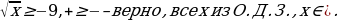
Более сложные задания сводятся к типовым. Например, для неравенства 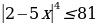 «условие» выполняется. Оно эквивалентно неравенству
«условие» выполняется. Оно эквивалентно неравенству 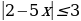 . Или № 150 (б) из
. Или № 150 (б) из 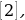 с.297:
с.297: 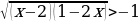 .
.
Пример соответствует последней клетке типовой таблицы. Имеем 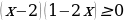 .
.
Очевидно, уравнения 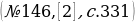
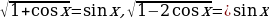 равносильны, соответственно системам
равносильны, соответственно системам 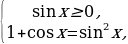
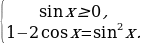
 Можно теперь предложить учащимся доказать теорему 1, используя метод возведения обеих частей в квадрат равенства (1). Например,
Можно теперь предложить учащимся доказать теорему 1, используя метод возведения обеих частей в квадрат равенства (1). Например, 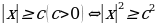
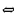
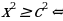
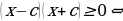
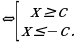
Иррациональные неравенства 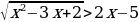 и
и 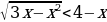
равносильны, соответственно, совокупности и системе
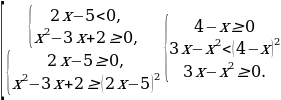
По свидетельству [5], около 52,5 не справились с заданием типа В вида:
зная, что 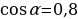 и
и 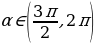 , найти
, найти 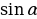 .
.
Предлагаем, в соответствии с изложенным выше, следующую цепочку рассуждений: 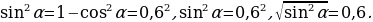 Так как в четвертой четверти
Так как в четвертой четверти 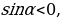 то
то 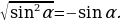 Следовательно,
Следовательно, 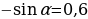 .
.
Ответ. 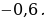
5. Правило умножения или деления обеих частей на выражения. Считаем, дети должны уметь пользоваться тремя тезисами:
Тезис 1. Если в обеих частях равенства или неравенства имеется одинаковое выражение, то обе части надо разделить на него, при этом:
Тезис 2. Надо отдельно рассмотреть случай, когда выражение может равняться нулю – на нуль делить нельзя!
Тезис 3. В неравенствах надо знать знак выражения – знак не знаешь – нельзя ни делить, ни умножать.
Рассмотрим примеры.
1. Решить уравнение (задание типа С1 из КИМов ЕГЭ).
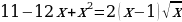 .
.
Решение. Так как уравнение 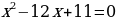 имеет корни 1 и 11, то
имеет корни 1 и 11, то 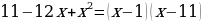 и исходное уравнение принимает вид
и исходное уравнение принимает вид 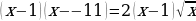
1случай. 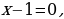
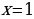 подходит.
подходит.
2 случай. 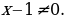 Делим обе части на
Делим обе части на 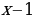 :
: 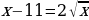 . Пусть
. Пусть 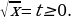 Тогда
Тогда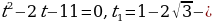 не подходит,
не подходит, 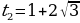 . Значит,
. Значит, 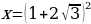 .
.
Ответ. 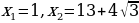 .
.
2. Решить неравенство: 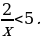
Решение. Знак 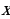 не знаем – умножать обе части на
не знаем – умножать обе части на 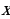 нельзя. Решение обычно сводят к методу интервалов:
нельзя. Решение обычно сводят к методу интервалов:
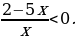
Но, можно, зная, что 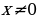 обе части умножить на
обе части умножить на 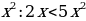 .
.
Еще лучше решить неравенство перебором знаков 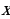 . Если
. Если 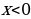 , то
, то 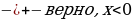 подходит.
подходит.
Если 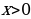 , то умножаем на обе части на
, то умножаем на обе части на 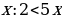
Ответ. 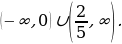
3. Решить неравенство: 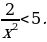
Решение. 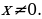 Умножаем обе части на
Умножаем обе части на 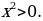
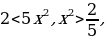
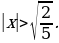
Ответ. 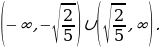
Другие примеры: №144 г), №135, №150 г), №151 г). 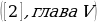 .
.
Рассмотрим №135 г).
Решить неравенство: 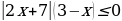 .
.
Решение. 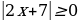 .
.
1случай. 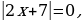
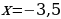 подходит.
подходит.
2 случай. 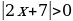 . Делим обе части на
. Делим обе части на 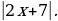 Получится
Получится 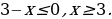
Ответ. 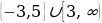 .
.
В заключение разберем задания С3 и С5 из КИМов 2013 г., где по ходу решения используются рассмотренные базовые понятия.
Задание С3 (2013г.). Решить систему неравенств:
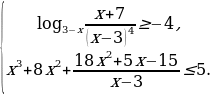
Решение. 1) Решаем первое неравенство системы. Находим О.Д.З.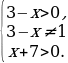
Р ешение системы изобразим схематически
ешение системы изобразим схематически




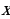
-7 2 3
Так как 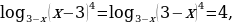 то неравенство принимает вид
то неравенство принимает вид 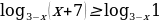 ⇔
⇔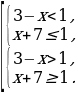 ⇔
⇔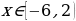 .
.
2) Решаем второе неравенство на множестве 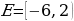 .
.
Здесь 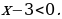 Умножаем обе части неравенства на
Умножаем обе части неравенства на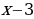 . После элементарных преобразований получим
. После элементарных преобразований получим 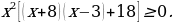
1случай. 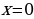 подходит.
подходит.
2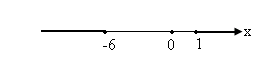 случай.
случай. 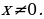 Делим обе части на
Делим обе части на 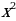 :
: 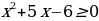 . Корни соответ-
. Корни соответ-
ствующего уравнения 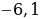 .
.
Так как уравнение решаем на 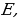 то
то 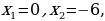 или
или 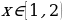 .
.
Ответ. 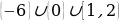 .
.
Задание С5 (2013г.). Найдите все значения параметра 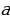 , при каждом из которых уравнение
, при каждом из которых уравнение 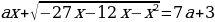 имеет единственный корень.
имеет единственный корень.
Решение. Обычно такие задачи решают графическим способом. В работе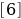 показано, что задание можно выполнить путем сведения уравнения к равносильной системе
показано, что задание можно выполнить путем сведения уравнения к равносильной системе 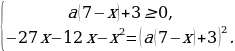
Не будем повторять дальнейшие выкладки из 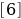 , где рассматриваетcя другой подобный пример.
, где рассматриваетcя другой подобный пример.
Литература
1. Алгебра и начала математического анализа, 10-11 кл., под ред. А.Н. Колмогорова, М.: Просвещение, 2012г.
КИМы ЕГЭ по математике, 2007-2009 гг.
КИМы ЕГЭ по математике, 2013, №104.
Новым стандартам нестандартный подход. Методические рекомендации / Сост. Лазарева Л.А. – М.: УЦ «Перспектива», 2012. – 36с.
Ященко И.В. и др. Подготовка к ЕГЭ по математике 2012г.
Умаханов А.Я. Анализ решений задач с параметром из КИМ ЕГЭ по математике, Научно-методический журнал «Модернизация образования», №3/2013, с.88-90, Махачкала, ДИПКПК.
Эфендиев Э.И., Загиров Н.Ш., Насруллаев Н.Б. Принцип однозначности функции и одно его следствие, Научно-методический журнал «Модернизация образования», №1/2011, с.36-40, Махачкала, ДИПКПК.







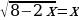 , возведением обеих частей в квадрат получить значения
, возведением обеих частей в квадрат получить значения 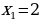 ,
, 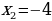 и, затем проверкой отбросить «лишний корень»
и, затем проверкой отбросить «лишний корень» 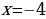 (принцип «действовать и думать»), то в духе новых стандартов сначала ученик, подумав, должен заметить, что
(принцип «действовать и думать»), то в духе новых стандартов сначала ученик, подумав, должен заметить, что 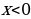 не может быть корнем уравнения и, следовательно, уравнение эквивалентно системе
не может быть корнем уравнения и, следовательно, уравнение эквивалентно системе 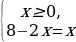 (принцип «думать и действовать»).
(принцип «думать и действовать»).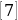 .
.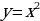 и
и 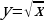 лежит функция
лежит функция 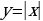 . Вот пример определения
. Вот пример определения 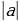 .
.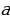 ;
;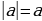 ; если же знак «
; если же знак «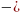 », то пиши
», то пиши 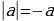 .
.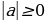 для любого
для любого 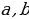 :
: 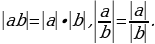
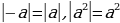 (1)
(1)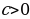 . Тогда
. Тогда  )
) 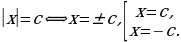
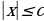 ⇔
⇔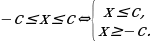
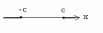
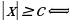
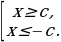
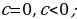 неравенства вида
неравенства вида 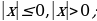 демонстрировать возможности использования теоремы на примерах решения неравенств вида:
демонстрировать возможности использования теоремы на примерах решения неравенств вида: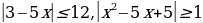 .
.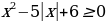 можно решить не только «снятием» модуля, но и его «одеванием»:
можно решить не только «снятием» модуля, но и его «одеванием»: 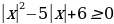 .
.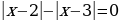 легче решить возведением обоих частей равенства
легче решить возведением обоих частей равенства 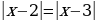 в квадрат:
в квадрат: 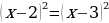 .
.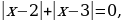
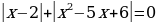 .
.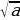 найди такое число
найди такое число 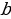 , что:
, что: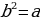 . Таким образом,
. Таким образом, 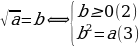
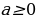 .
.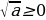 .
.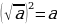 .
.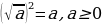 . Следовательно, у функции
. Следовательно, у функции 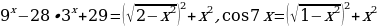 и учащиеся теряли 1 балл из двух, когда забывали о том, что
и учащиеся теряли 1 балл из двух, когда забывали о том, что 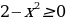 или
или 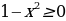 .
. 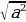 .
.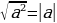 , а предложить с виду длинное правило.
, а предложить с виду длинное правило.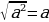 ,
,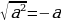 ;
;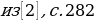
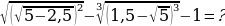 и др.
и др.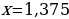
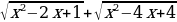
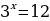
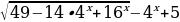
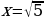
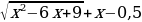
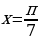
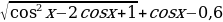
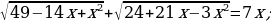
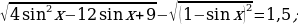
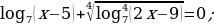
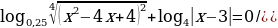
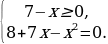
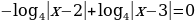
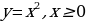 или непосредственной проверкой. Рекомендуем иметь в кабинете плакат.
или непосредственной проверкой. Рекомендуем иметь в кабинете плакат.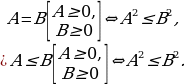
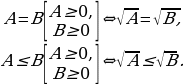
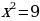
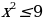
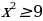
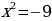
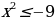
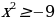
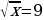
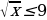
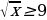
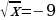
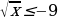
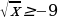
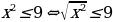 . Знак
. Знак 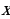 не знаем, следовательно,
не знаем, следовательно, 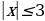 . Применяем 2) из теоремы 1:
. Применяем 2) из теоремы 1: 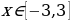 . Если
. Если 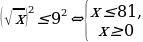
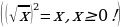 . Если же
. Если же 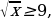 то
то 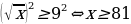 .
.
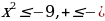
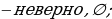
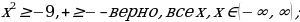
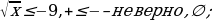
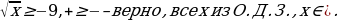
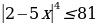 «условие» выполняется. Оно эквивалентно неравенству
«условие» выполняется. Оно эквивалентно неравенству 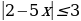 . Или № 150 (б) из
. Или № 150 (б) из 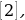 с.297:
с.297: 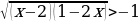 .
.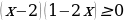 .
.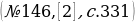
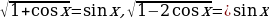 равносильны, соответственно системам
равносильны, соответственно системам 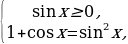
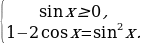
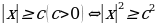
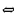
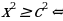
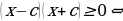
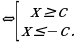
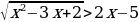 и
и 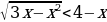
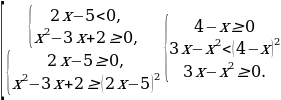
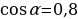 и
и 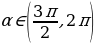 , найти
, найти 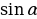 .
.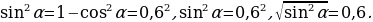 Так как в четвертой четверти
Так как в четвертой четверти 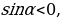 то
то 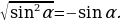 Следовательно,
Следовательно, 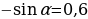 .
. 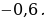
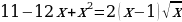 .
.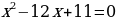 имеет корни 1 и 11, то
имеет корни 1 и 11, то 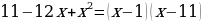 и исходное уравнение принимает вид
и исходное уравнение принимает вид 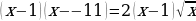
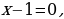
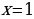 подходит.
подходит.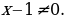 Делим обе части на
Делим обе части на 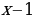 :
: 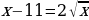 . Пусть
. Пусть 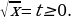 Тогда
Тогда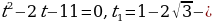 не подходит,
не подходит, 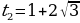 . Значит,
. Значит, 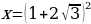 .
.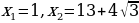 .
.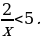
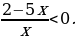
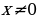 обе части умножить на
обе части умножить на 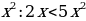 .
.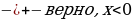 подходит.
подходит.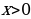 , то умножаем на обе части на
, то умножаем на обе части на 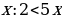
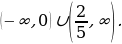
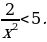
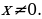 Умножаем обе части на
Умножаем обе части на 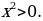
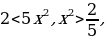
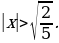
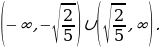
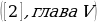 .
.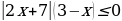 .
.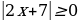 .
.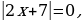
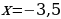 подходит.
подходит.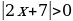 . Делим обе части на
. Делим обе части на 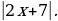 Получится
Получится 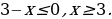
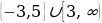 .
.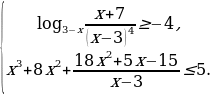
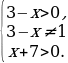
 ешение системы изобразим схематически
ешение системы изобразим схематически

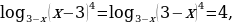 то неравенство принимает вид
то неравенство принимает вид 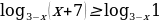 ⇔
⇔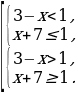 ⇔
⇔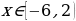 .
. 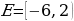 .
.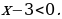 Умножаем обе части неравенства на
Умножаем обе части неравенства на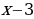 . После элементарных преобразований получим
. После элементарных преобразований получим 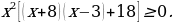
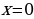 подходит.
подходит.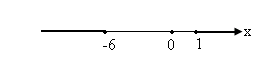 случай.
случай. 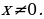 Делим обе части на
Делим обе части на 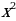 :
: 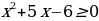 . Корни соответ-
. Корни соответ-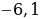 .
.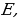 то
то 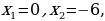 или
или 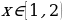 .
. 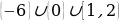 .
.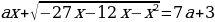 имеет единственный корень.
имеет единственный корень.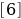 показано, что задание можно выполнить путем сведения уравнения к равносильной системе
показано, что задание можно выполнить путем сведения уравнения к равносильной системе