Просмотр содержимого документа
«Конспект урока по геометрии в 8 классе на тему: "ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ"»
Урок 3
ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
Цели: доказать первый признак подобия треугольников.
Ход урока
I. Проверка домашнего задания.
1. № 543.
Решение
1) Пусть 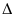 АВС
АВС 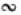
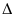 А1В1С1, с коэффициентом подобия k, АН и А1Н1 – высоты.
А1В1С1, с коэффициентом подобия k, АН и А1Н1 – высоты.
2) 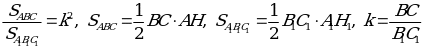 .
.
3) Имеем 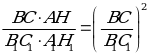 или
или 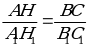 .
.
2. Выполнить устно:
| а) 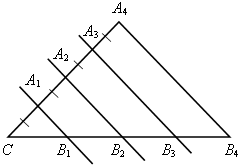 | СА1 = А1А2 = А2А3 = А3А4 А1В1 || А2В2 || А3В3 || А4В4 СВ4 = 12 см, 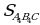 = 32 cм2. = 32 cм2. Найдите: а) В1В2, В2В4; б) 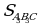 . . |
| б)  | ВС = 6 см. Найти: а) ВD и СD; б) SАСD : SАВD.
|
в) SАВС = 36 см2.
Найти:
а) SCMN; б) SAKN; в) SВMNK.
II. Изучение нового материала.
Доказательство первого признака подобия треугольников.
III. Закрепление изученного материала.
№ 550.
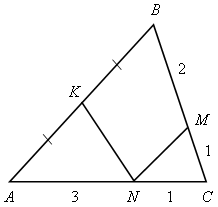
| а) 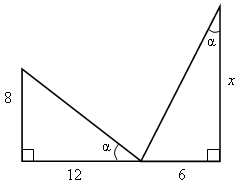 | Решение Данные прямоугольные треугольники подобны (по двум углам). 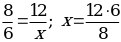 = 9. = 9.
|
| б) 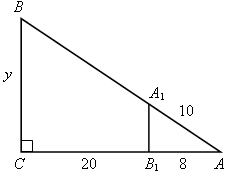 | А1В1 = 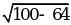 = 6. = 6. 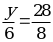 ; 8y = 28 ∙ 6; y = 21. ; 8y = 28 ∙ 6; y = 21.
|
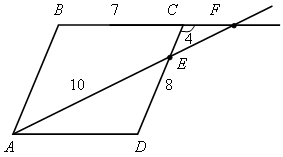
№ 551 (а).
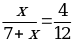 ; 12x = 4x + 28; х = 3,5.
; 12x = 4x + 28; х = 3,5.
СF = 3,5 см.
2) СF = y, 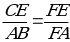 ;
; 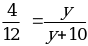 ;
;
12у = 4у + 40; у = 5.
EF = 5 см.
№ 553 (а), № 561 – устно.
IV. Итоги урока.
1. Для того чтобы записать пропорциональность сторон подобных треугольников, нужно:
1) выяснить, при каких вершинах углы равны;
2) определить, какие стороны являются сходственными (лежат против равных углов);
3) записать пропорцию, где в числителях – стороны одного треугольника, в знаменателях – сходственные им стороны другого.
2. В подобных треугольниках сходственные стороны пропорциональны сходственным высотам.
Домашнее задание: вопросы 1–5, с. 160; №№ 551 (б), 552 (а), 553 (б).
Для желающих.
На чертеже изображен шлагбаум, закрывающий проезд через железнодорожное полотно. На сколько опустится короткий конец шлагбаума, если больший поднимается на 2 м?
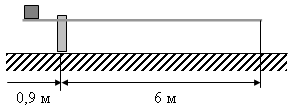
| 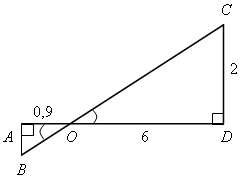 | Решение 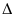 AВО AВО 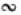 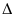 DСО. DСО. 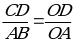 ; ; 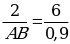 ; ; 6AB = 2 ∙ 0,9; AB = 0,3. |







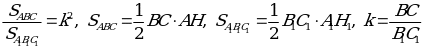 .
.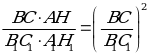 или
или 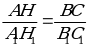 .
.




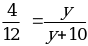 ;
;

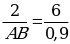 ;
;









