Вариант 1 КР № 10
1. Выполните действие: а) –3,8–5,7 б) –8,4+3,7 в) 3,9–8,4 г) –2,9+7,3 д) 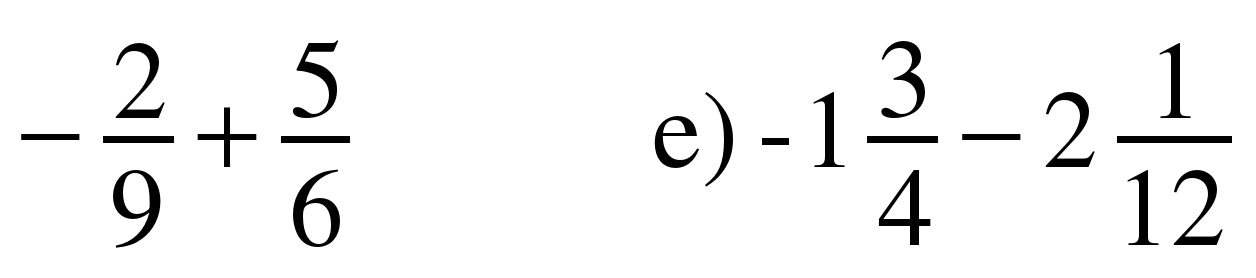
2. Найдите значение выражения (–3,7–2,4)–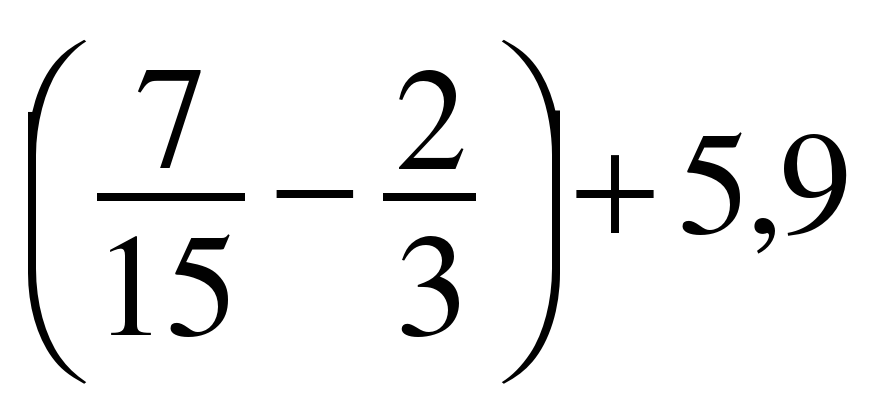
3. Решите уравнение: а) х+3,12=–5,43; б) 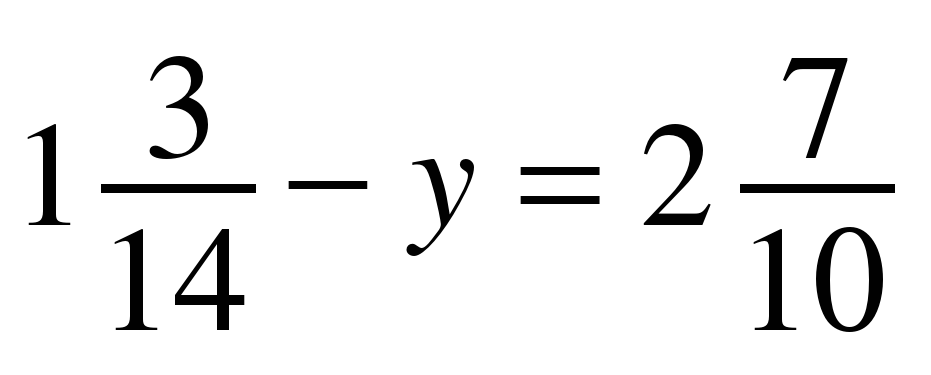
4. Найдите расстояние между точками А(–2,8) и В(3,7) на координатной прямой.
5. Напишите все целые значения n, если 4n|
Вариант 1 КР № 10
1. Выполните действие: а) –3,8–5,7 б) –8,4+3,7 в) 3,9–8,4 г) –2,9+7,3 д) 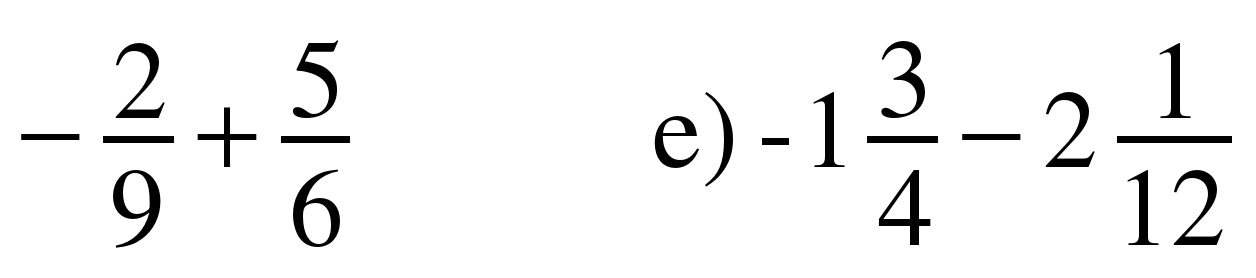
2. Найдите значение выражения (–3,7–2,4)–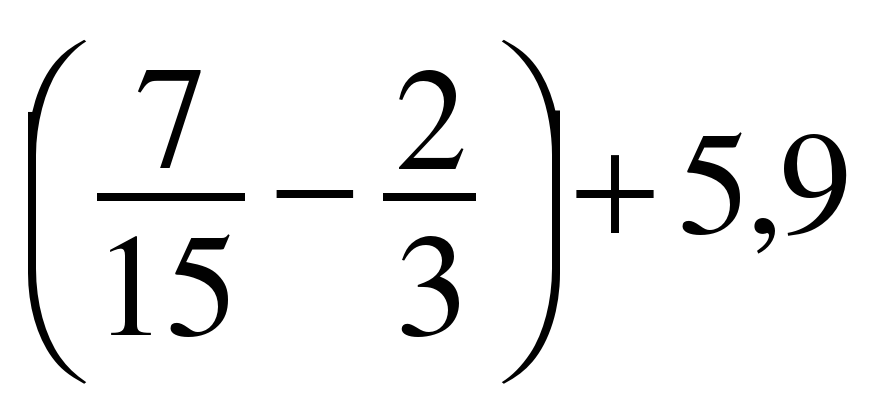
3. Решите уравнение: а) х+3,12=–5,43; б) 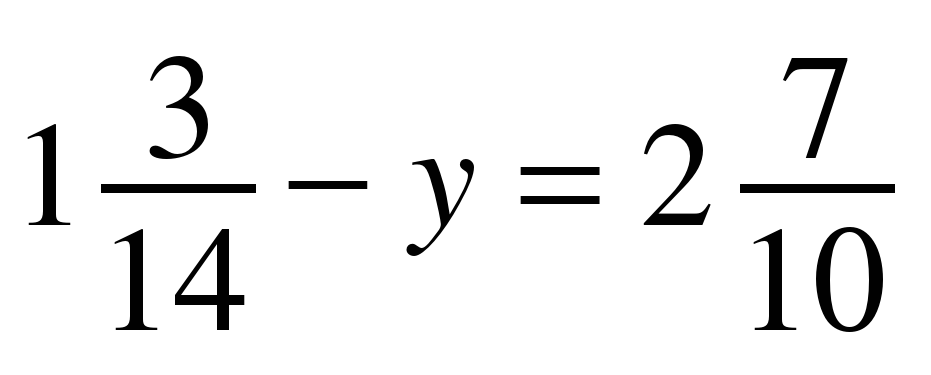
4. Найдите расстояние между точками А(–2,8) и В(3,7) на координатной прямой.
5. Напишите все целые значения n, если 4n|
Вариант 1 КР № 10
1. Выполните действие: а) –3,8–5,7 б) –8,4+3,7 в) 3,9–8,4 г) –2,9+7,3 д) 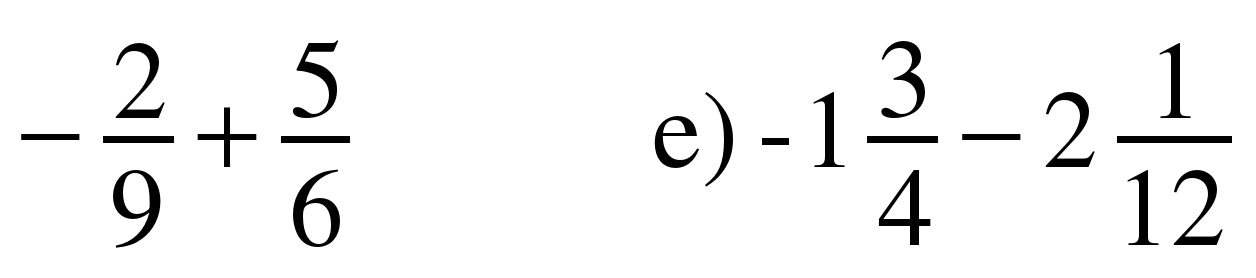
2. Найдите значение выражения (–3,7–2,4)–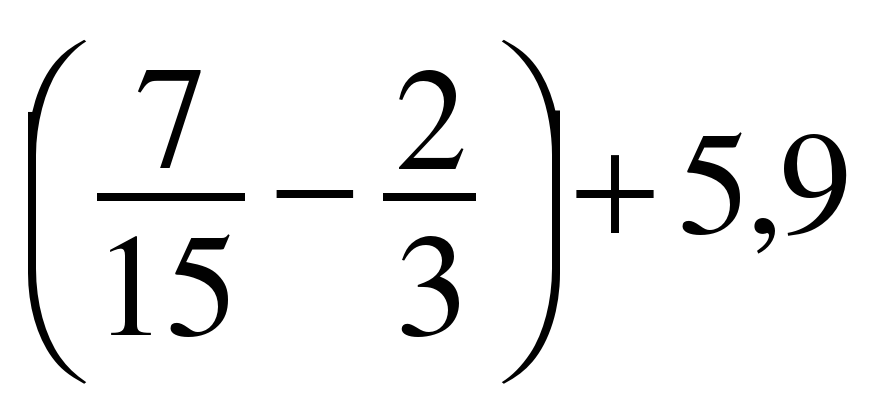
3. Решите уравнение: а) х+3,12=–5,43; б) 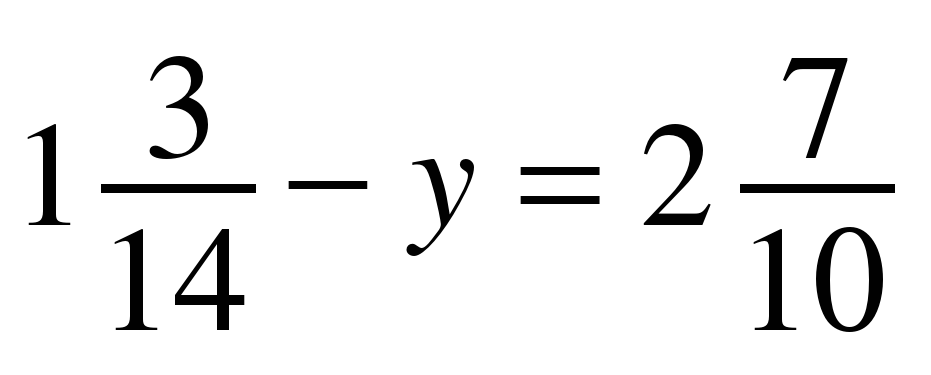
4. Найдите расстояние между точками А(–2,8) и В(3,7) на координатной прямой.
5. Напишите все целые значения n, если 4n|
Вариант 2 КР № 10
1. Выполните действие: а) –3,5+8,1 б) –7,5+2,8 в) –2,9–3,6 г) 4,5–8,3 д) 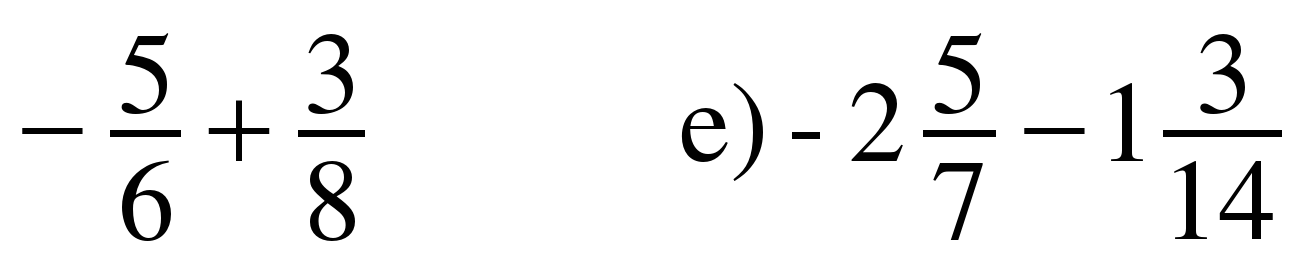
2. Найдите значение выражения 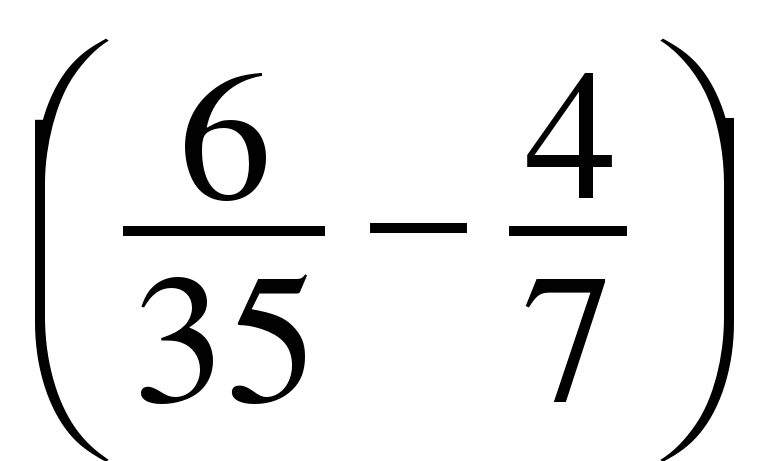 –(–1,8–4,3)–5,7
–(–1,8–4,3)–5,7
3. Решите уравнение: а) 5,23+х= –7,24; б) 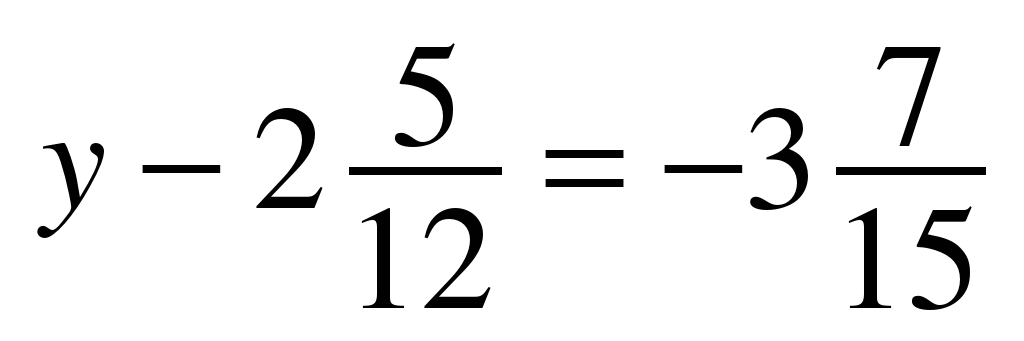
4. Найдите расстояние между точками С(–4,7) и Р(–0,8) на координатной прямой.
5. Напишите все целые значения у, если 2
Вариант 2 КР № 10
1. Выполните действие: а) –3,5+8,1 б) –7,5+2,8 в) –2,9–3,6 г) 4,5–8,3 д) 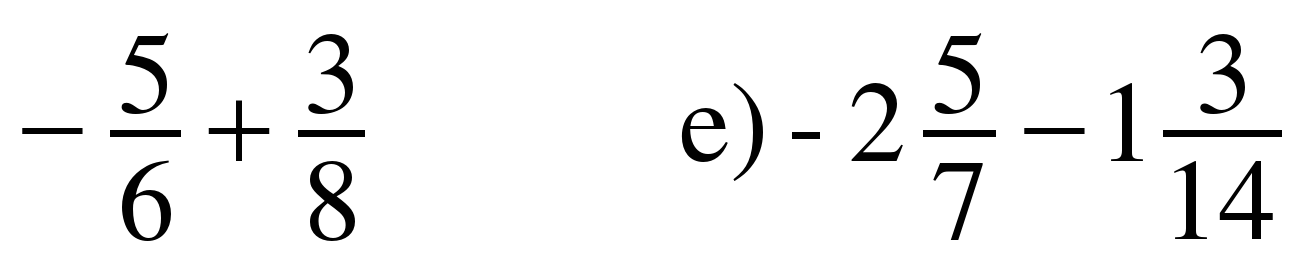
2. Найдите значение выражения 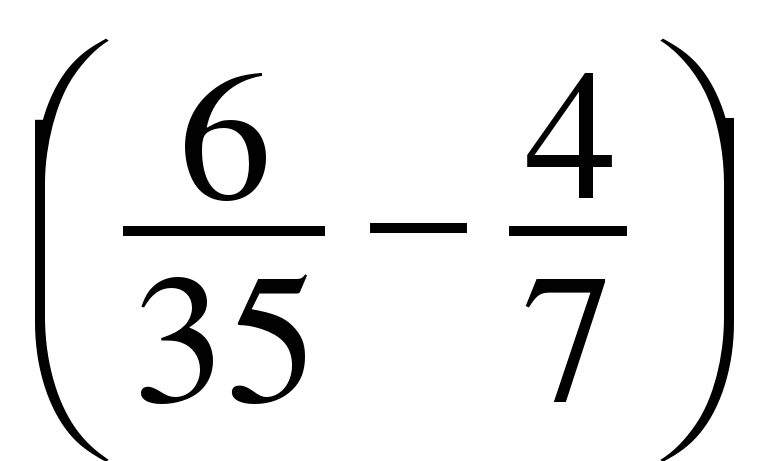 –(–1,8–4,3)–5,7
–(–1,8–4,3)–5,7
3. Решите уравнение: а) 5,23+х= –7,24; б) 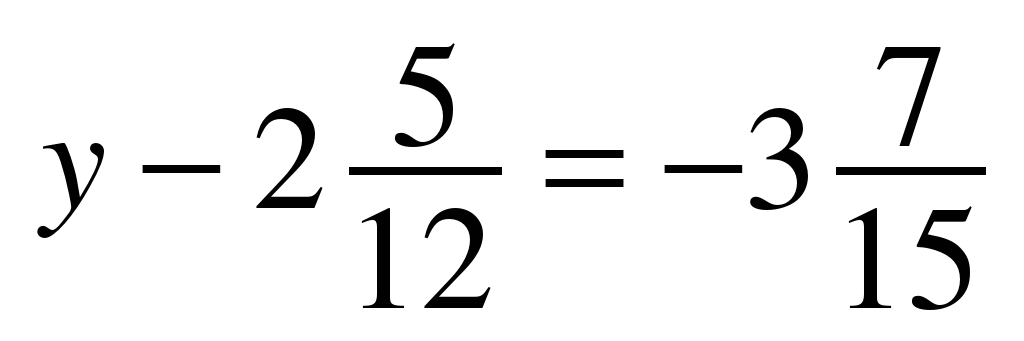
4. Найдите расстояние между точками С(–4,7) и Р(–0,8) на координатной прямой.
5. Напишите все целые значения у, если 2
Вариант 2 КР № 10
1. Выполните действие: а) –3,5+8,1 б) –7,5+2,8 в) –2,9–3,6 г) 4,5–8,3 д) 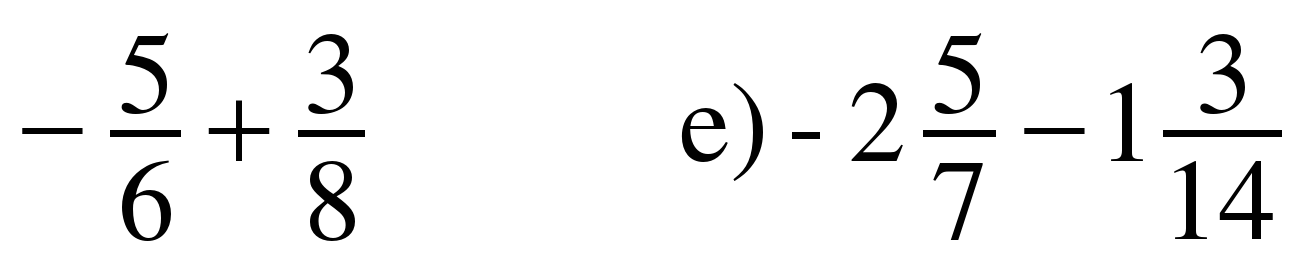
2. Найдите значение выражения 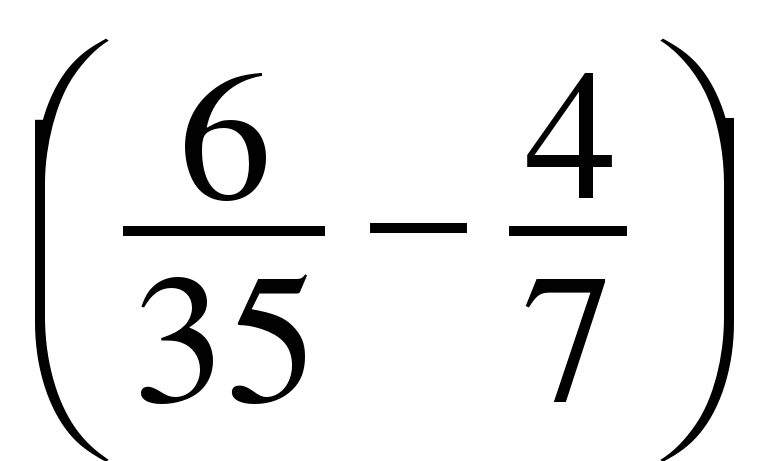 –(–1,8–4,3)–5,7
–(–1,8–4,3)–5,7
3. Решите уравнение: а) 5,23+х= –7,24; б) 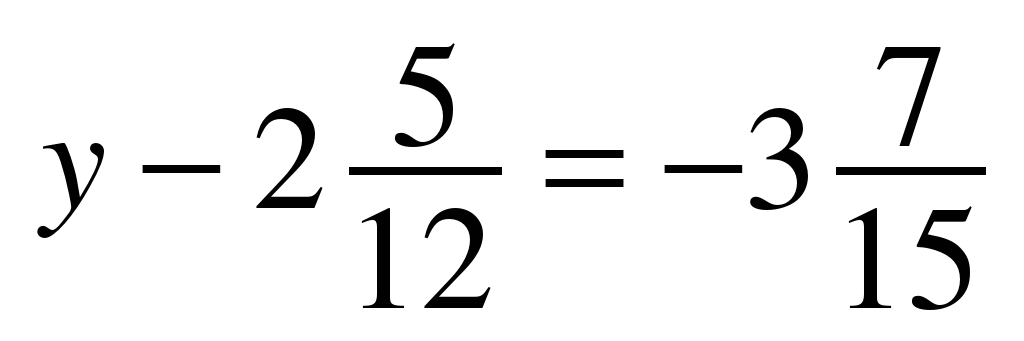
4. Найдите расстояние между точками С(–4,7) и Р(–0,8) на координатной прямой.
5. Напишите все целые значения у, если 2















