МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №11» ИЗОБИЛЬНЕНСКОГО ГОРОДСКОГО ОКРУГА СТАВРОПОЛЬСКОГО КРАЯ
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ПО ФИЗИКЕ
ОТ ТЕОРИИ К ПРАКТИКЕ
|
Автор: Газимагомедова К.А. учитель физики высшей квалификационной категории
|
пгт. Рыздвяный 2023 г
Содержание
Введение……………………………………………………………………….3
1.Методы решения качественных задач……………………………………..6
2. Методы решения экспериментальных задач……………………………...7
3. Методы решения вычислительных задач……………………………….…8
3.1 Арифметический метод………………………………………………….8
3.2 Алгебраический метод…………………………………………………...9
3.3 Геометрический метод…………………………………………………..10
4. Методы решения графических задач………………………………………11
5. Функциональные роли задач при обучении физике с примерами……….14
6. Алгоритмический способ решения задач…………………………………..18
Заключение…………………………………………………………………..…20
Список литературы………………………………………………………….…23
Приложения…………………………………………………………………….24
Введение
Что такое физическая задача? С точки зрения психологии, задача – это проблема, которая заключается в несоответствии между требованиями задачи и знаниями субъекта, и для её решения субъект должен включить творческую мыслительную деятельность.
Такое определение влечёт весьма широкое понимание слова «задача». Американский математик Д. Пойа писал: «Основная часть нашего сознательного мышления связана с решением задач. Когда мы не развлекаемся и не мечтаем, наши мысли направлены к какой-то конечной цели, мы ищем пути и средства к достижению этой цели, мы пытаемся выработать какой-то курс, следуя которому можно достичь нашей конечной цели» (Пойа Д. Как решать задачу.)
Если при постановке проблемы сразу ясен путь её решения, то задачи не возникает; если такого пути не видно, то это – задача. Таким образом, задача предполагает необходимость сознательного поиска соответствующего средства для достижения ясно видимой, но непосредственно недоступной цели.
В методике под физической задачей понимают проблему, решаемую с помощью логических умозаключений, математических действий, эксперимента на основе законов и методов физики.
Каждая задача содержит информационную часть, условие и требование-вопрос. Информационная часть может быть достаточно богатой, поэтому само содержание задачи позволяет знакомить с историей, с достижениями техники, сообщать сведения из других наук.
Решение задач по физике - необходимый элемент учебной работы. Образовательное, политическое и воспитательное значение задач в курсе физики средней школы трудно переоценить. Без решения физических задач, курс физики не может быть усвоен. В большинстве школ решению физических задач уделяется значительное внимание. Тем не менее, многие учащиеся постоянно испытывают затруднения в решении задач, что наглядно обнаруживается на ВПР и выпускных экзаменах. Это объясняется не только сложностью данного вида занятий для учащихся, но и недостатками в подборе и методике решения задач по школьному курсу физики.
Решение физических задач - один из основных методов обучения физике. С помощью решения задач сообщаются знания о конкретных объектах и явлениях, создаются и решаются проблемные ситуации, формируются практические и интеллектуальные умения, сообщаются знания из истории науки и технике, формируются такие качества личности, как целеустремленность, настойчивость, аккуратность, внимательность, дисциплинированность, развиваются эстетические чувства, формируются творческие способности. В период ускорения научно-технического прогресса на каждом рабочем месте необходимы умения ставить и решать задачи науки, техники, жизни. Поэтому важнейшей целью физического образования является формирование умений работать со школьной учебной физической задачей.
Задачи по физике классифицируют по многим признакам: по содержанию, целевому назначению, глубине исследования вопроса, способам решения, способам задания условия, степени трудности и т.д.
В своей работе я классифицирую задачи по способу решения. По способу решения различают устные (качественные), экспериментальные, вычислительные и графические задачи. Деление — это условно в том отношении, что при решении большинства задач применяют несколько способов. Например, при решении экспериментальной задачи необходимы устные рассуждения, а также во многих случаях вычисления и работа с графиками.
В работе я отдельно рассматриваю каждый способ решения и выделяю их особенности, кроме этого, я рассмотрю задачи простые и олимпиадного уровня.
ЦЕЛЬ: отбор методов решения физических задач разного уровня.
ЗАДАЧИ:
1. найти и изучить различные источники, содержащие описание методов решения физических задач;
2. отобрать наиболее рациональные методы решения физических задач разного уровня;
3. составить набор задач разного уровня для самостоятельного решения различными методами.
ОБЪЕКТ ИССЛЕДОВАНИЯ: физические задачи.
ПРЕДМЕТ ИССЛЕДОВАНИЯ: методы решения физических задач.
1. Методы решения качественных задач
Качественные задачи делятся на два вида: а) простые качественные задачи или, как их иногда называют, задачи-вопросы; б) сложные качественные задачи, представляющие как бы совокупность или комбинацию нескольких простых задач.
Решение качественной задачи обычно состоит в построении с помощью индукции и дедукции логических умозаключений, основанных на физических законах.
Схема решения качественных задач
Чтение условия задачи, выяснение всех терминов в условии задачи.
Анализ условия задачи, выяснение физических явлений, построение, если это потребуется, схемы или чертежа.
Построение аналитической и синтетической цепей рассуждений.
Анализ полученного ответа с точки зрения его физического смысла, соответствия условию и реальности.
Рассмотрим простую качественную задачу. Почему, споткнувшись, человек падает вперед?
Ответ: споткнувшийся человек падает вперед потому, что его ноги, задержанные каким-либо препятствием, останавливаются, а другие части тела по инерции продолжают движение вперед.
Рассмотрим сложную качественную задачу.
Как будут изменяться показания приборов в цепи (Приложение 2) при передвижении ползунка реостата влево? Вправо?
2. Методы решения экспериментальных задач
Характерной чертой этого типа задач является использование при решении эксперимента как лабораторного, так и демонстрационного.
Постановка опытов при решении демонстрационных экспериментальных задач должна удовлетворять всем условиям школьного демонстрационного эксперимента. При этом особое внимание нужно обращать на обеспечение хорошей видимости приборов и явлений. Это тем более необходимо, что к работе с приборами часто привлекаются вызванные к демонстрационному столу учащиеся, которые мало заботятся об этой чисто профессиональной стороне дела.
Решим одну из экспериментальных задач.
Задача: на концах равноплечного рычага подвешены два тела равной массы, но разного объема.
Сохранится ли равновесие, если тела опустить в воду?
Решение: при погружении тела в воду на него будет действовать выталкивающая сила. Ее величина пропорциональна объему тела и плотности жидкости. На меньшее по объему тело будет действовать меньшая выталкивающая сила. Поэтому в воде перетянет тело меньшего размера.
Как видим, эксперимент в этой задаче играет вспомогательную роль. Задача может быть решена и без него, но от этого она значительно проиграет.
Задача: найти величину силы, заставляющей гирьку массой 100г, подвешенную на нити длиной l = 60 см, вращаться в горизонтальной плоскости по окружности радиусом R= 20 см. расчеты проверить на опыте. Принять вес гирьки равным 1Н. (Приложение 3)
3. Методы решения вычислительных задач
Методы решения вычислительных задач зависят от многих причин: их сложности, математической подготовки учащихся, поставленных учителем целей и т.д.
В зависимости от применяемого математического аппарата различают следующие методы или способы решения вычислительных задач: арифметический, алгебраический и геометрический. По характеру логических операций, используемых в процессе решения, различают аналитический, синтетический и аналитико-синтетический методы.
3.1. Арифметический метод
При этом методе над физическими величинами производят только арифметические действия. Физические задачи решают примерно так же, как задачи на уроках арифметики: по вопросам, без применения формул. Арифметический способ применяют в основном на первой ступени обучения физике, когда учащиеся еще не имеют достаточных знаний по алгебре или еще не уяснили достаточно глубоко зависимость между величинами, входящими в физические формулы.
Иногда считают, что отличительная черта арифметического метода - отсутствие буквенных выражений. Дело как раз не в буквенных выражениях, а в том, что при этом методе не составляют и не решают уравнений. Приведем пример решения задачи арифметическим способом, но с применением буквенных выражений. Возьмем задачу на закон Архимеда, когда с буквенными обозначениями соответствующих величин учащиеся уже знакомы.
Какой максимальный груз может выдержать в пресной воде плот, связанный из 25 сосновых бревен. Объем каждого бревна составляет в среднем 0,8 м3.
Решение выполняем по вопросам.
Каков объем бревен плота? V= 0,8м3 х 25= 20м3.
Чему равна масса плота? По таблице находим, что масса 1м3 древесины равна 500кг. m = 500 кг х 20 = 10000 кг.
Каков вес плота? Р = 9,8н х 10000 - 98000н.
Чему равна масса вытесняемой воды при полном погружении плота в воду?
По таблице находим, что масса 1м3 воды равна 1000 кг.
m = 1000 кг · 20 =20000 кг.
Каков вес вытесненной воды? Р = 9,8Н/кг х 20000 кг = 196000 Н.
Чему равен вес груза? F = 196000 Н - 98000 Н - 98000 Н.
Огвет: 98000 Н.
3.2. Алгебраический метод
При этом методе применяют имеющиеся у учащихся знания по алгебре, используют формулы, составляют и решают уравнения. Наиболее простой случай применения алгебраического метода состоит в решении задач по готовой формуле.
Рассмотрим для примера следующие задачи:
Задача 1. Мотоцикл, масса которого вместе с мотоциклистом равна 240 кг., движется с ускорением а = 3 м/с2. Определите силу трения, действующую на мотоцикл.
Решение: силу трения находят по формуле F = mа (второй закон Ньютона). Получаем, что F = 240 х 3 = 720 Н. Ответ: 720 Н.
Задача 2. Равна ли сила атмосферного давления, действующая на пол, весу воздуха в комнате? Изменится ли давление в помещении, если его закрыть герметически?
Решение: При нормальном атмосферном давлении вес воздуха P=9,8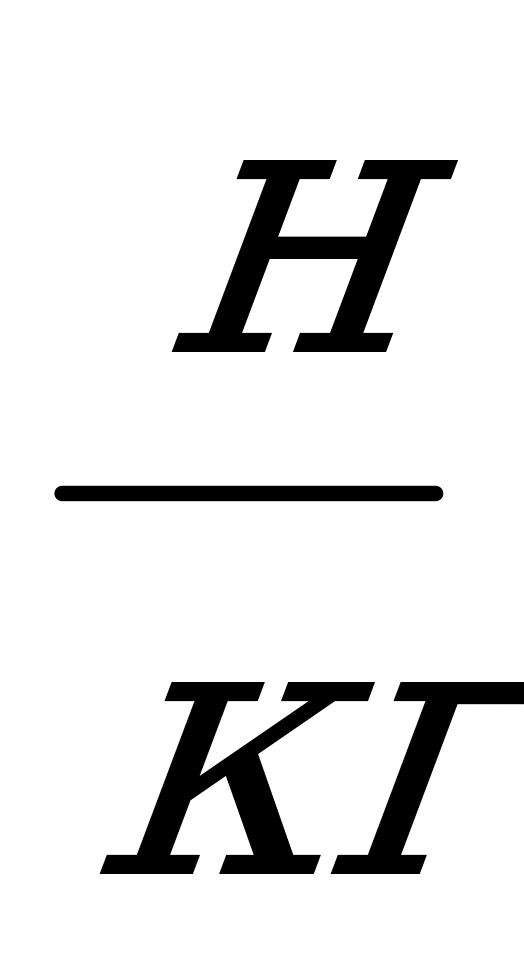
 m= =9,8
m= =9,8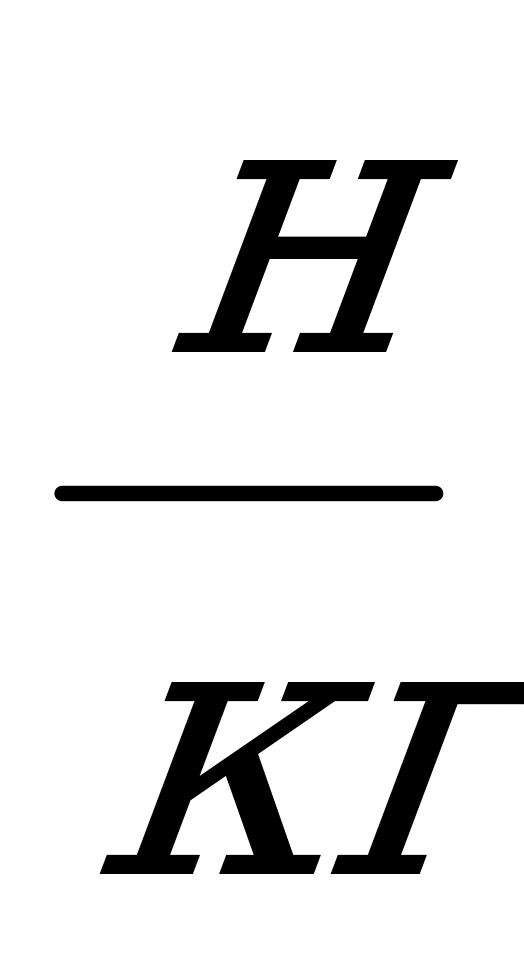
 pV=9,8
pV=9,8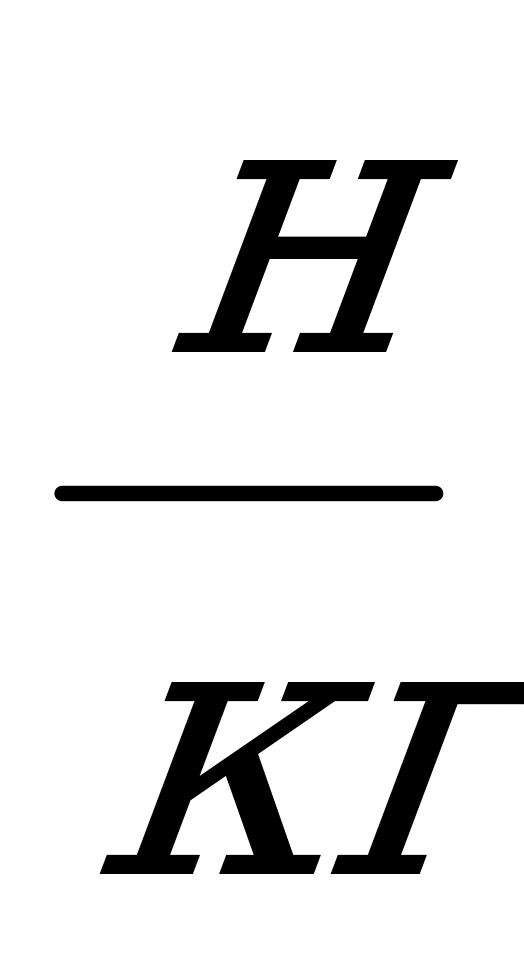
 1,29
1,29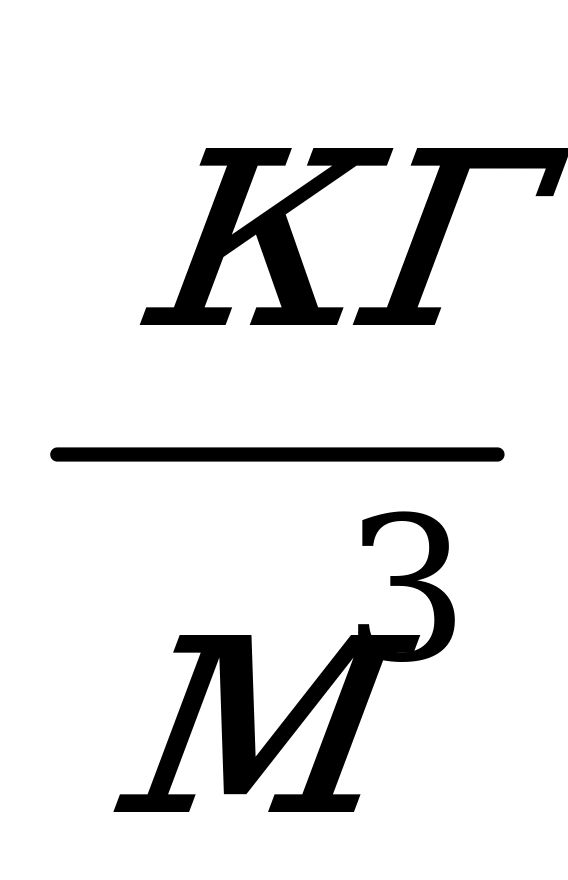
 V=9,8
V=9,8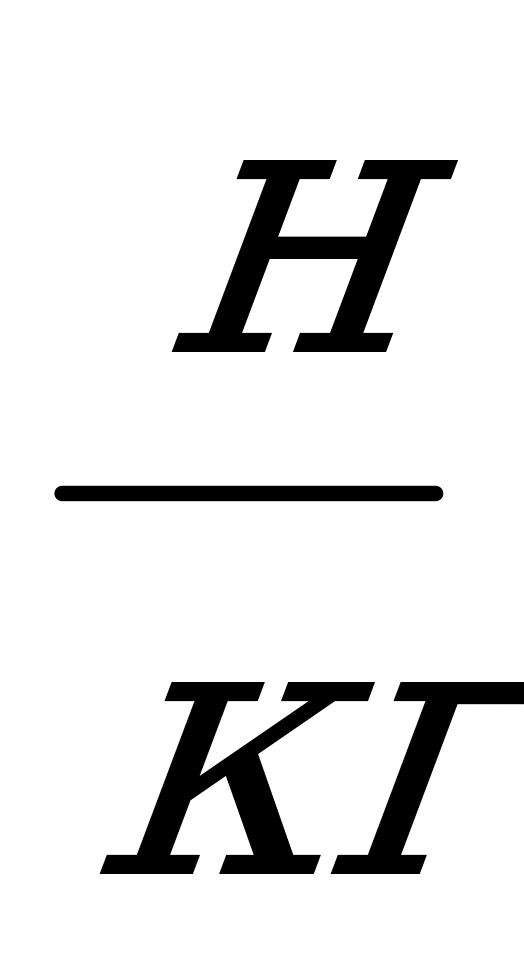
 1,29
1,29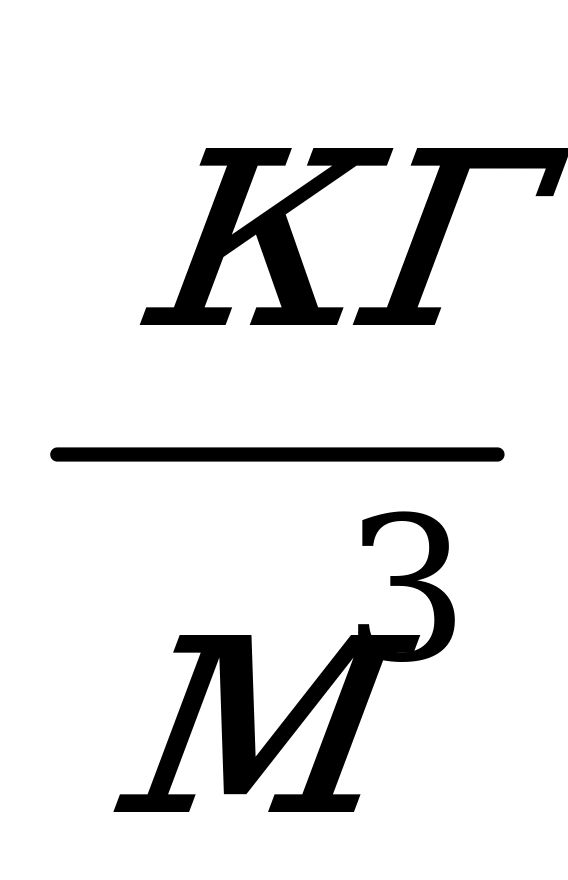
 Sh, где S- площадь пола, выраженная в м2 , a h - высота комнаты в метрах.
Sh, где S- площадь пола, выраженная в м2 , a h - высота комнаты в метрах.
Сила давления F = 100000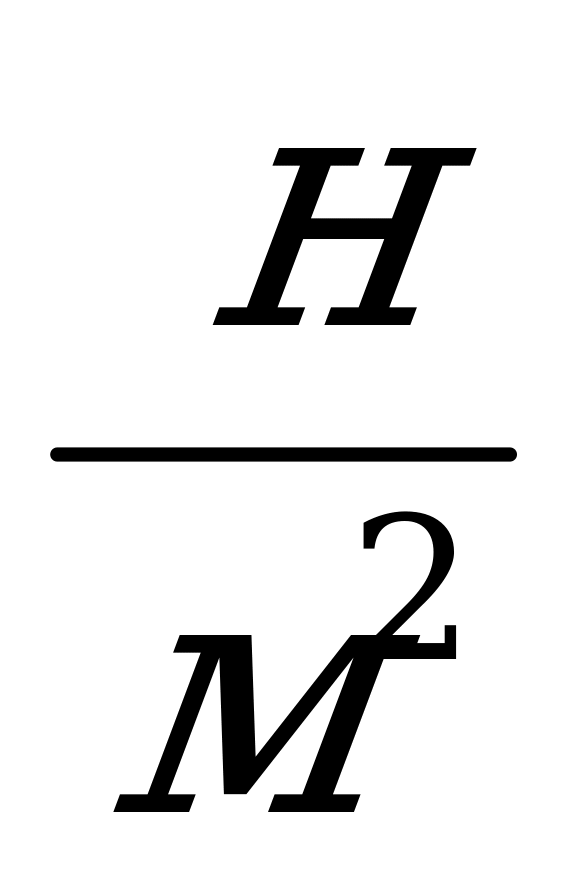
 S.
S.
Так как высота h 3-5 м, то F» P.
3-5 м, то F» P.
Давление воздуха обусловлено ударами молекул. При одной и той же плотности и температуре воздуха его давление будет одним и тем же и в открытом и в герметически закрытом помещении.
3.3. Геометрический метод
При решении задач геометрическим методом искомую величину находят на основании известных учащимся геометрических соотношений, геометрический метод широко применяют в статике, геометрической оптике, электростатике и других разделах курса физики средней школы.
Приведем пример решения задач геометрическим методом.
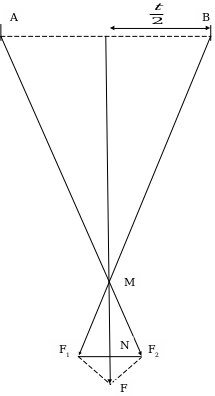
Задача 1. Посредине троса длиной 1=10м подвесили фонарь массой m=10 кг. Определить силу натяжения троса, если стрела прогиба h = 0,5 м. (Приложение 4 и 5).
Задача 2. Фонарь массой М = 10 кг подвешен над серединой улицы шириной l = 10 м на канатике, допустимая сила натяжения которого Т = 500Н. Определить высоту Н крепления концов канатика, если точка крепления фонаря должна находиться на высоте h=5м. (Приложение 6)
4. Методы решения графических задач
Графическими называют задачи, в которых объектом исследования являются графики зависимости физических величин. В одних задачах эти графики заданы в условии, в других - их надо построить.
Основные этапы решения графических задач следующие. Если график зависимости между величинами дан, то надо осмыслить его, разобрать характер зависимости на участке. Пользуясь масштабом, необходимо по графику получить искомые величины. Если график зависимости не дан, то по условию задачи, или по значениям, взятым из специальных таблиц, строят график. Для этого чертят оси координат, выбирают определенный масштаб на них, составляют таблицы, а после этого наносят на плоскость с координатными осями точки с соответствующими ординатами и абсциссами. Соединяя данные точки, получают график зависимости между физическими величинами и затем исследуют его, как было указано выше.
Для примера рассмотрим следующую задачу.
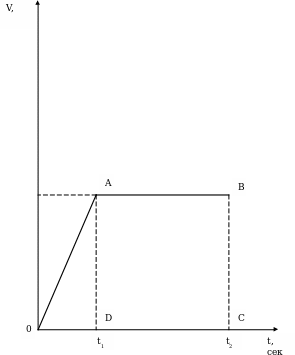
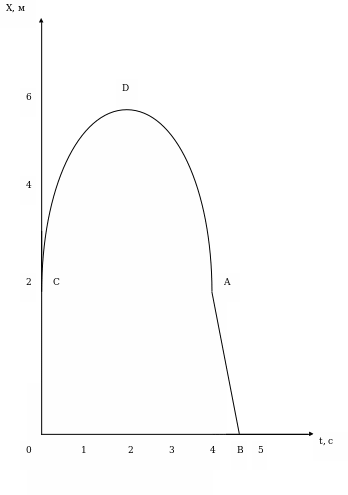
По графику (Приложение 7) описать движение тела, определить время, путь и ускорение на отдельных участках пути.
Анализируя график, учащиеся должны, во-первых, установить, что он выражает зависимость скорости от времени. Начальная скорость тела v=0. к моменту времени t=t тело приобрело скорость v. от момента времени t=0 до t=t скорость увеличивалась. На графике приведена зависимость скорости v от времени t, следовательно, тело двигалось равноускоренно. В промежутке времени t — t скорость не изменялась. Тело двигалось равномерно. Определим ускорение для промежутка времени (0-t). v =a t, отсюда а =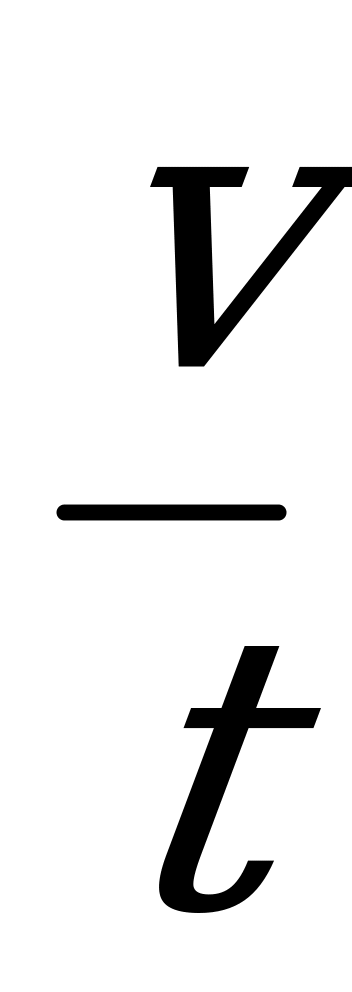 . для промежутка времени t - t ускорение а=0. путь s, пройденный телом при равноускоренном движении за время t численно равен площади треугольника OAD.
. для промежутка времени t - t ускорение а=0. путь s, пройденный телом при равноускоренном движении за время t численно равен площади треугольника OAD.
S=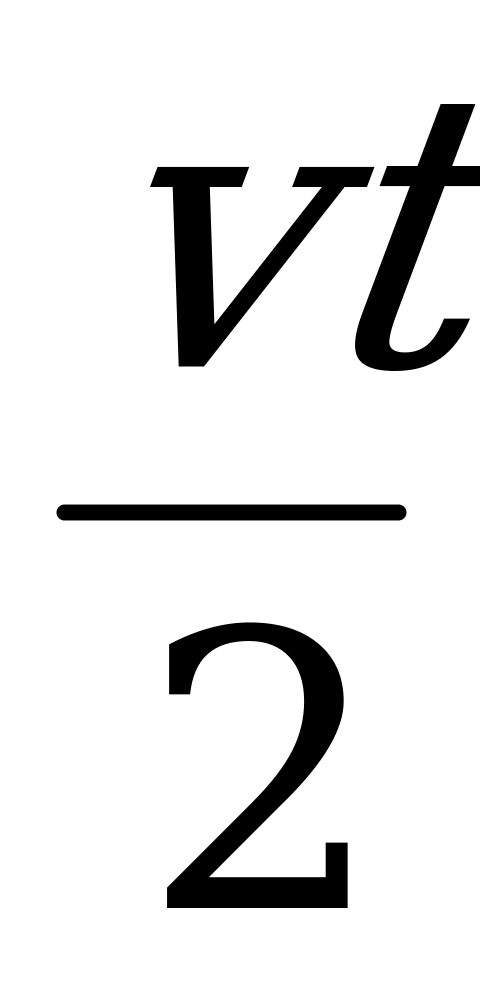 =
=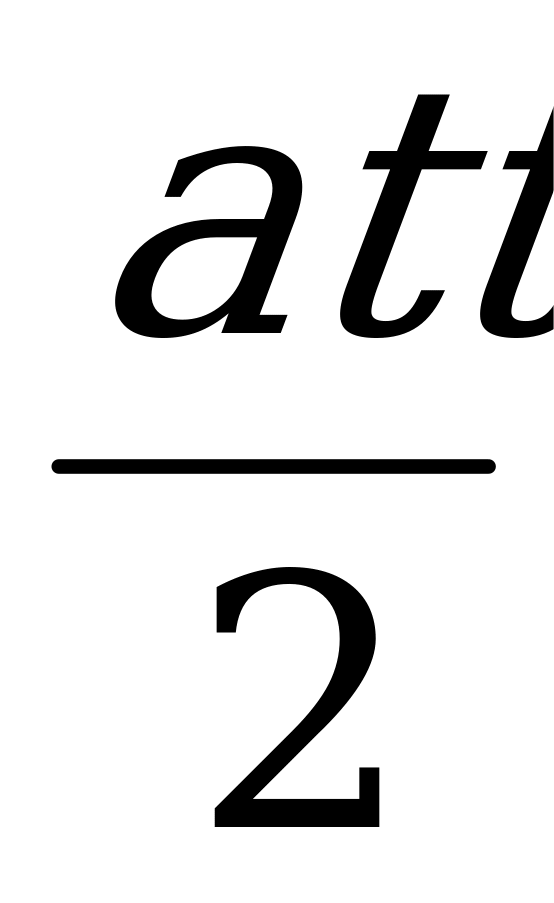 =
=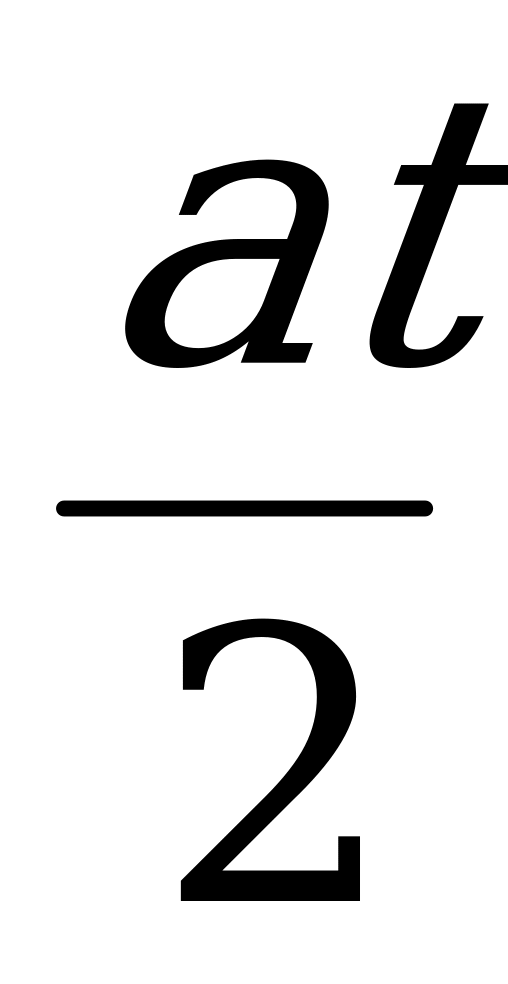
Таким образом, с помощью графика получена важная формула пути для равноускоренного при условии, если начальная скорость равна 0.
Путь s за время t численно равен площади трапеции ОАВС:
S=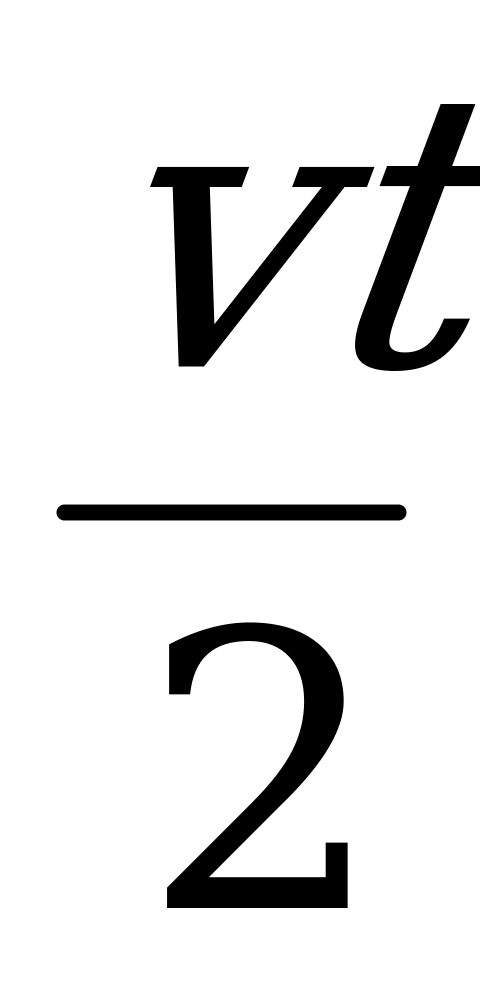 +v(t - t)=
+v(t - t)=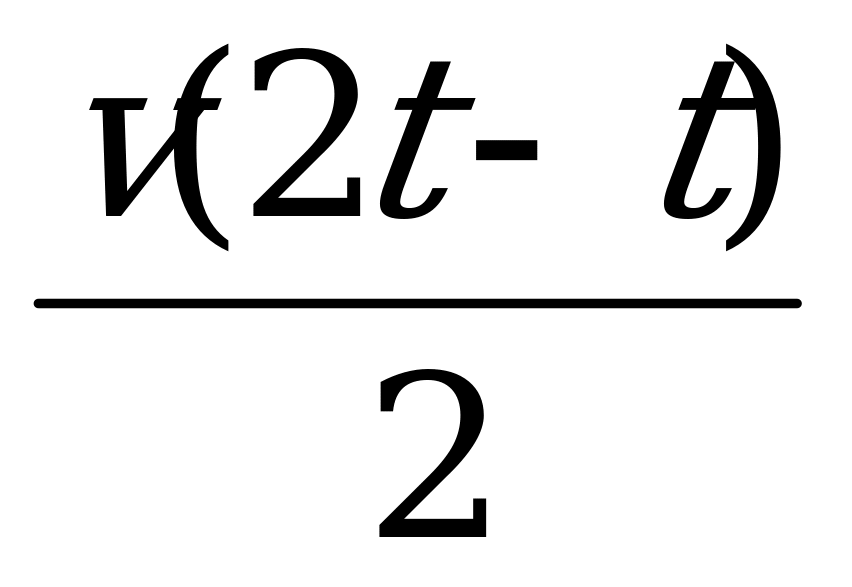 .
.
Графические задачи в вариантах ВПР
Рассмотрим примеры для 7,8 и 11 классов.
На рисунке приведён график зависимости скорости электропоезда метро от времени при движении между двумя станциями. Сколько секунд поезд двигался с постоянной скоростью? Ответ запишите в секундах.
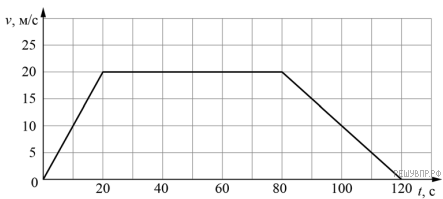
Решение.
Из графика следует, что скорость тела неизменна в интервале времени от 20 до 80 с. Значит, равномерное движение длилось 60 с.
2. По результатам нагревания кристаллического вещества массой 5 кг построен график зависимости температуры этого вещества от количества подводимого тепла. Считая, что потерями энергии можно пренебречь, определите, какое количество теплоты потребовалось для нагревания 1 кг этого вещества в жидком состоянии на 1 °C? Ответ запишите в джоулях.
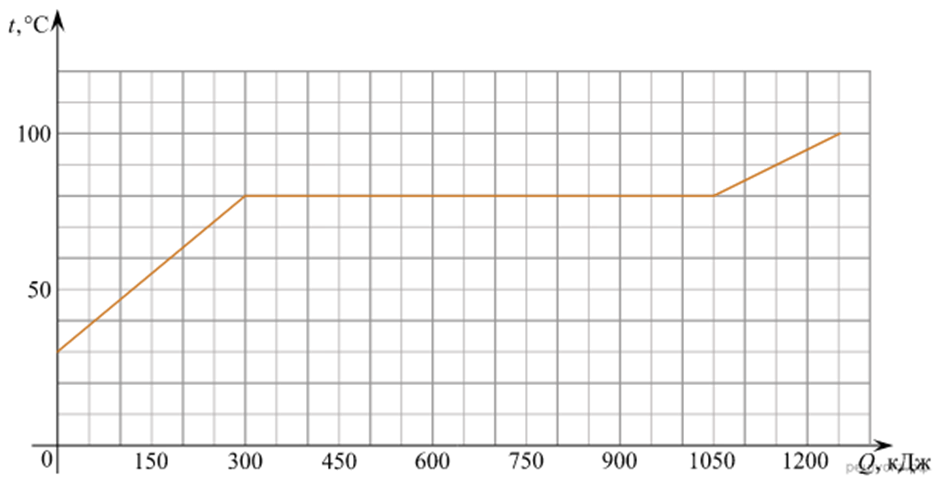
Решение.
Вещество находилось в жидком состоянии после горизонтального участка, соответствующего плавлению. Из графика находим, что для нагревания пяти кг вещества от 80 °С до 100 °С потребовалось 1250 – 1050 = 200 кДж. Следовательно, удельная теплоёмкость этого вещества в жидком состоянии равна
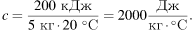
Количество теплоты, требуемое для нагревания 1 кг этого вещества в жидком состоянии на 1 °C, равно 2000 Дж.
Мотоциклист движется по прямой улице. На графике представлена зависимость его скорости от времени.
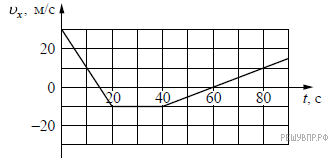
Проанализируем утверждения:
1) В промежутке времени от 20 до 40 с равнодействующая сил, действующих на мотоциклиста, сообщает ему постоянное по модулю ускорение, отличное от нуля. Утверждение неверно.
2) В течение первых 20 с мотоциклист двигался равноускоренно, а в течение следующих 20 с — равномерно. Утверждение верно.
3) Модуль максимальной скорости мотоциклиста за весь период наблюдения составляет 72 км/ч. Утверждение неверно.
4) В момент времени 60 с мотоциклист остановился, а затем начал движение в противоположном направлении. Утверждение верно.
5) Модуль максимального ускорения мотоциклиста за весь период наблюдения равен 4 м/с2. Утверждение неверно.
Функциональные роли задач при обучении физике с примерами
Ниже приведены некоторые функциональные роли задач при обучении физике с примерами.
1. При изложении нового учебного материала. Для более глубокого понимания явления свободного падения тел после выяснения характера данного движения решается задача:
С балкона на высоте 25 м над землей вертикально вверх брошено тело со скоростью 20 м/с.
(Задача не содержит вопроса, условие служит лишь отправной точкой для рассуждений, смысл такой задачи – распознать явление, рассмотреть его со всех возможных сторон, выявить существенные детали. После обсуждения ученики сами формулируют интересующие их вопросы, ответы на которые (решения) отыскиваются сообща.)
Вопросы для обсуждения (ставит учитель):
Можем ли мы сообщить какому-либо телу скорость 20 м/с?
Реальна ли данная ситуация?
Можно ли бросить тело «вертикально» вверх?
Будет ли это движение свободным падением? Почему?
Чем пренебрегаем в данной ситуации?
Как движется тело? Вверх? Вниз? И т.п.
Выполняется рисунок на доске (ось, уровень земли, начальная координата, начальная скорость, ускорение). Записываются законы y(t) и uy(t). Обсуждается смысл записанных уравнений.
Ученики задают следующие вопросы:
Где будет тело через 1, 2, … секунды? Какова его скорость в эти моменты времени?
Когда тело будет на высоте 40 м, 50 м, 20 м?
(Идет отработка навыков обращения с уравнениями y(t) и uy(t). Обсуждаются результаты и их смысл.)
На сколько метров тело поднимется?
(Решается, по сути, стандартная задача: найти максимальную высоту подъема тела, брошенного вертикально вверх. Вопрос записывается в тетрадь, высказываются предположения, ученики «сами» придумывают, как найти hmax. Необходимые записи делаются своевременно на доске учителем.)
Когда и с какой скоростью тело упадет на землю?
(Строятся графики зависимостей y(t) и uy(t), сопоставляются с результатами вычислений.)
2. Вместо изложения новой темы. На 3-м или 4-м уроке в IX классе вместо изложения тем «Проекции вектора на координатные оси», «Равномерное прямолинейное движение» решается следующая задача:
Тело переместилось из точки А с координатами (–3 м; 4 м) в точку В с координатами (5 м; –2 м) за 4 секунды.
(Задача не имеет вопроса, задана некорректна: многое недосказано. Однако, рассмотрев с учащимися возможные варианты, останавливаемся на прямолинейном движении с постоянной скоростью).
Вычерчивается рисунок (система координат, точки А и Б, вектор перемещения). По ходу «вбрасываются» элементы нового материала: проекции вектора перемещения, как их найти, их смысл, знаки проекций и их смысл. Находится модуль перемещения. Все новые определения, формулы записываются в тетрадь и выделяются. Выясняется смысл понятий «равномерное» движение, «скорость». Находится модуль скорости по условию задачи, проекции скорости, выясняется их смысл. Получаются законы движения x(t), y(t); уравнение траектории у(х). Чертятся графики функций x(t), y(t), у(х). Данная задача решается практически весь урок. Учитель лишь направляет ход мыслей учащихся в нужное русло. У детей создается ощущение, что они сами «придумали» все «это» (т. е. способ описания равномерного прямолинейного движения).
Аналогично можно «исключить» изложение нового материала по темам: «Сила Лоренца», «Кинематика гармонических колебаний», «Резонанс в электрической цепи», «Явление радиоактивного распада», «Искусственные спутники Земли» и др.
3. Перед изучением новой темы. В VII классе перед изучением темы «Архимедова сила» полезно решить задачу:
Брусок размерами 20×20×20 (см) опустили под воду на глубину 10 см.
(Задача без вопроса. Основная цель решения задачи перед изучением темы – «прочувствовать» ситуацию, получить выводы, на которые будем опираться при изучении темы. Выводы должны быть понятны всем — это залог успешного усвоения предстоящей темы.)
Обсуждается неоднозначная ситуация: как можно осуществить реально условие задачи. В результате появляется рисунок (брусок целиком в воде, глубина погружения, по договоренности, – расстояние от поверхности воды до верхней параллельной ей грани бруска). Далее рассчитываются силы, с которыми вода давит на грани бруска; эти силы сравниваются, ученики формулируют выводы (равнодействующая отлична от нуля, направлена вверх, боковые силы уравновешены). Выясняется, какие еще силы действуют на брусок (имеется в виду сила тяжести). Обсуждение приводит к необходимости знать плотность вещества бруска. Для примера предполагается, что брусок сделан из а) дерева; б) металла. Находится сила тяжести в каждом случае, она сравнивается с равнодействующей сил давления воды, делаются выводы (сплошное тело с плотностью, большей, чем плотность жидкости, тонет в ней; с плотностью, меньшей, чем плотность жидкости, всплывает). Задача решается весь урок в «активном» режиме.
4. Закрепление в процессе знаний, обобщение изученного. По теме «Свойства паров. Влажность воздуха» предлагается задача:
Имеется сосуд, содержащий воздух при температуре 17°С и влажности 60%. Как сделать водяной пар в сосуде насыщенным?
(Это комплексная задача с неявным вопросом: неясно, что нужно найти. Суть: «придумать» способ насыщения пара и сформулировать минизадачу, затем ее решить.)
Строится график зависимости давления насыщенного пара от температуры; наносится точка, описывающая данное состояние пара; отыскиваются способы его насыщения. Рассматриваются все возможности: изобарное охлаждение, увеличение массы влаги, изотермическое сжатие, изохорное охлаждение. Все варианты предлагают и обосновывают ученики. По ходу обсуждается реальность осуществления каждого из вариантов, необходимые для этого условия. Изучается возможность каждого процесса в реальной жизни (в квартире, на улице и т. д.). Процессы изображаются графически. В результате решения одной задачи отрабатываются умения и навыки по данной теме, актуализируются знания, происходит их более полное и глубокое усвоение.
5. Проверки для усвоения учебного материала. Для проверки знаний, умений и навыков учащихся используются в основном такие формы работы, как самостоятельная, проверочная, контрольная работы. Отличительная черта задач, входящих в задания данных работ, – преимущественно репродуктивный характер самих задач. Этап проверки по сути – выявление степени их соответствия требованиям образовательного стандарта. Здесь задачи не средство обучения, их решение есть показатель осознанности и глубины знаний. Однако важно такие задания дифференцировать. Можно подготовить разноуровневые варианты, что мне, кажется, не совсем целесообразным (сильный ученик данную ему учителем сильную задачу со словами: «Ты должен это решить», – может и не решить; как оценить его труд, ведь уровень задачи явно выше требований стандарта). Эффективнее будет давать такие задания, которые содержат относительно большое число вопросов – шагов решения одной большой задачи.
Алгоритмический способ решения задач по физике
Рассмотрим задачу из ЕГЭ под номером 30.
Грузы массами M и m = 1 кг связаны лёгкой нерастяжимой нитью, переброшенной через блок, по которому нить может скользить без трения (см. рис.). Груз массой M находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту α = 30°, коэффициент трения µ = 0,2). Чему равно минимальное значение массы M, при котором система грузов ещё не выходит из первоначального состояния покоя.
Какие законы Вы используете для описания равновесия тел? Обоснуйте их применение к данному случаю.

1) Масса М будет минимальной в том случае, если сила трения, действующая на брусок, будет направлена вниз вдоль наклонной плоскости. Изобразим силы, действующие на каждое тело. Так как нить легкая, то T1 = T2 = T.
2) Запишем второй закон Ньютона для обоих тел
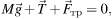
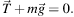
Найдем проекции на оси координат:
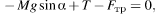
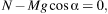
T −
mg = 0- для второго тела, движущегося по вертикали Учитывая, что F
тр=µ N, и объединяя формулы, получаем:
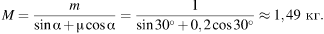
Заключение
Основные средства учителя, позволяющие научить решать задачи:
1) Образец решения задачи. Такой образец полезен на первом этапе, но его дидактическая ценность невелика.
2) Алгоритмическое предписание. По такому предписанию легко решаются задачи, например, в кинематике.
Но сложные творческие задачи не решаются по образцу или алгоритмическому предписанию. Для их решения учащиеся сами должны «изобрести» (составить) способ решения. А для этого:
Они должны знать и владеть общими эвристическими методами их решения. Эти общие методы следует сообщать учащимся постепенно и регулярно, иллюстрируя достаточным числом примеров.
Больше решать задач самостоятельно, т. к. любые умения и навыки приобретаются только в практике. При этом решение задач учениками должно быть мотивированным, т. к. эффективность поиска решения прямо зависит от стремления его найти.
Поэтому добавим ещё два средства:
3) Обучение эвристическим методам решения задач на большом числе примеров.
4) Самостоятельное и заинтересованное решение учащимися задач, способ решения которых им не известен, но материал которых не выходит за рамки их знаний.
Значительное влияние на формирование интереса учащихся к физическим знаниям оказывает историзм в обучении, принятый как важный принцип сообщения учебного материала.
Интерес подкрепляется также в тех случаях, когда обучаемые четко понимают практическую необходимость получаемых знаний для дальнейшей жизни.
Значительно повышается интерес обучаемых за счет организации познавательной деятельности, рассчитанной на увеличение самостоятельной работы, включение разнообразных заданий поискового характера, создание проблемных ситуаций.
Любой неожиданный результат при решении задачи, любое предположение, опровержение, несоответствие и т. п. могут стать основой появления проблемной ситуации и разрешения возникшей проблемы.
Хотелось бы остановиться на использовании задач для создания проблемных ситуаций. Само слово «задача» на многих языках звучит как «проблема». Чтобы задача заинтересовала, ее содержание должно быть продумано, актуально, любопытно. Основная цель решения задач на уроках физики состоит в том, чтобы учащиеся глубже понимали физические закономерности, суть рассматриваемых явлений. С другой стороны, только решая задачи, можно научиться их решать. Поэтому должна быть очевидной двойственность роли задач в процессе изучения физики: процесс решения задач есть показатель результативности обучения, он же – средство обучения, средство развития способностей мыслительной деятельности.
Большинство задач, приведенных в упражнениях учебников физики, имеет репродуктивный характер (хотя и такие нужны на первоначальном этапе) и, по сути, задачами не являются. Действительно, нельзя назвать задачей задание на подстановку чисел в формулу, выражение из формулы «буквы» с последующей подстановкой данных. К сожалению, учителя часто ограничиваются подобными упражнениями при изучении темы. При таком подходе физика явлений «уходит» на второй план, а о развитии детей не приходится и говорить. Непонятно, зачем вообще в таком случае решать задачи, это пустая трата времени.
В данной работе я исследовала методы решения задач, выделила уровни, что дает возможность научиться решать задачи разного уровня (Приложение 1), находить более рациональные способы и приемы их решения.
В заключении предлагаю памятку для решения задач по физике:
Внимательно прочить условие задачи, уяснить какой физический процесс или явление в ней описывается.
Полностью записать условие задачи в столбик, необходимые константы и сформулировать вопрос задачи.
Перевести данные в систему СИ.
Сделать сопроводительный чертеж или схему, поясняющие задачу.
Начать решать задачу можно:
а) с вопроса задачи;
б) с записи основного закона, которому посвящена данная задача;
в) если в задаче дан КПД, то с записи КПД.
Используя физические законы и формулы, решить задачу в общем виде, не делая промежуточных вычислений, т.е. получить конечную формулу в буквенном выражении.
Проверить правильность полученной формулы с помощью размерностей; подставить в полученную формулу единицы измерения всех входящих в нее величин в системе СИ; произвести над ним соответствующие действия и получить правильную единицу измерения искомой величины.
Подставить в полученную формулу значения всех заданных величин, выраженных в системе СИ, произвести расчет.
Оценить ответ на физическую реальность.
Точность полученного результата не должна превышать точности исходных данных задачи.
Список литературы
Антипин, И.Р.Экспериментальные задачи по физике в 7-8 классах.–М. : Просвещение, 2013.–90с.
Знаменский, К.Н. Cборник задач по физике в средней школе. – М.: Наука, 2012. –135с.
Каменcкий, С.В.. Методика решения задач по физике в средней школе.– М.: Просвещение, 2013.–420с.
Крутецкий, В.А. Основы методики преподавания физики в средней школе.–М.: Просвещение, 2014.–254с.
Ланге, В.Н.. Экспериментальные физические задачи на смекалку. – М. :
Наука,2014. –120с.
Лукашик, В.И.. Физическая олимпиада. – М. : Просвещение, 2015. –110с.
Муравьев, А.В. Как учить школьников самостоятельно приобретать знания по физике. – М.:Просвещение, 2015.-160с.
Слобедецкий,И.Щ.. Всесоюзные олимпиады по физике. – М. : Просвещение, 2014.– 67с.
Тарасов, А.Н.. Вопросы и задачи по физике.– М.: Высшая школа, 2014.–104с.
Тульгинский, М.Е. Качественные задачи по физике в 7-8 классах.–М.:Просвещение,2016.–90с.
Приложение 1
Задачи для самостоятельного решения
1. Качественные задачи
Почему даже в спокойном воздухе распространяются запахи?
Почему для быстрой засолки огурцов их заливают подогретым соляным раствором?
Почему интенсивность броуновского движения возрастает с повышением температуры?
Почему твердые тела, состоящие из огромного числа молекул, сохраняют свою форму и не рассыпается на отдельные частицы?
Куда и почему наклоняются пассажиры в автобусе, когда он: тормозит? поворачивает вправо? поворачивает влево?
2. Экспериментальные задачи
На дно стакана положите кусок сахара, а затем осторожно налейте в стакан воды. Через некоторое время проверьте, станет ли вода сладкой не только внизу, но и наверху. Как объяснить это явление с молекулярной точки зрения?
Возьмите два стакана, один стакан наполните густым раствором марганцовокислого калия, а другой- чистой водой. Возьмите стеклянную трубку, со гнутую в виде буквы П , наполните ее чистой водой, зажав пальцами, переверните и опустите один ее конец в раствор, а другой - в чистую воду. Наблюдайте за ходом диффузии каждый день.
Положите один кусок сахара в стакан с холодной, а второй - с горячей водой. Какой кусок растворится быстрее и почему?
Существуют ли силы притяжения между молекулами жидкости? Поясните свое утверждение примерами и опытами.
Передвигая с помощью палочки пробку в картофельном пистолете, наблюдайте за уменьшением объема воздуха. Проделайте аналогичный опыт, наполняя трубку водой. Объясните разницу в сжимаемости воды и воздуха на основе молекулярного строения веществ.
3 Вычислительные задачи. Арифметический метод
3.1 Автомобиль «Чайка» развивает скорость до 160 км/ч, а почтовый голубь
- 16м/сек. Сможет ли голубь обогнать автомобиль?
Сколько бы потребовалось бы времени для того, чтобы уложить в ряд
кубики, объемом 1 мм3 каждый, взятые в том количестве, сколько содержится их в 1м3 , если на укладку одного кубика затрачивается время, равное 1с?
Брусок квадратного сечения со стороной квадрата, а имеет массу m = 40 кг. Какой станет масса бруска, если длину его увеличить в два раза, а каждую сторону квадрата уменьшить в два раза?
3.4 Девочки сделали снеговика, а мальчики соорудили точную его копию, но в два раза большей высоты. Какова масса копии, если масса оригинала равна 50 кг?
3.5 Железная и алюминиевая детали имеют одинаковые объемы. Найдите массы этих деталей, если масса железной детали на 12,75г больше массы алюминиевой.
4 Вычислительные задачи. Алгебраический метод
4.1 За какое время пробежит конькобежец расстояние в 100м, если он буде двигаться со скоростью 12 м/сек.?
4.2 Площадь боковой поверхности куба, сделанного из некоторого сплава металлов, равна 150 см2. После нагревания куба каждое его ребро стало длиннее на 1 мм. На сколько изменится объем куба?
4.3 Масса сплошного куба, сделанного из некоторого вещества, равна 2,5кг. Какую массу будет иметь этот куб, если длину ребра его уменьшить в два раза?
4.4 Определите плотность стекла, из которого сделан куб массой 857,5г, если площадь всей поверхности куба равна 294см2.
5 Вычислительные задачи. Геометрический метод
5.1 Два заряда по 25нКл каждый, расположенные на расстоянии 24см друг от друга, образуют электростатическое поле. С какой силой это поле действует на заряд 2нКл, помещенных в точку, удаленную на 15см от каждого из зарядов, если заряды, образующие поле, одноименны? Если заряды разноимённые?
5.2 В начале урока две одинаковые стальные гильзы, подвешенные на закрепленных в одной точке очень длинных нитях, были заряжены одноименными равными зарядами и разошлись на некоторое расстояние, много меньшее длины нитей. К концу урока расстояние между гильзами уменьшилось в 4 раза. Какая часть заряда стекла с каждой гильзы? Считать, что гильзы потеряли одинаковые заряды.
5.3 При внесении заряженного металлического шарика, подвешенного на изолирующей нити, в однородное горизонтальное направленное поле нить образовала с вертикалью угол 45градусов. На сколько уменьшится угол отклонения нити при стекании с шарика одной десятой доли его заряда?
5.4*Одинаковые шарики, подвешенные на закрепленных в одной точке нитях равной длины, зарядили одинаковыми одноименными зарядами. Шарики оттолкнулись, и угол между нитями стал равен  =60°. После погружения шарика в жидкий диэлектрик угол между нитями уменьшился до
=60°. После погружения шарика в жидкий диэлектрик угол между нитями уменьшился до 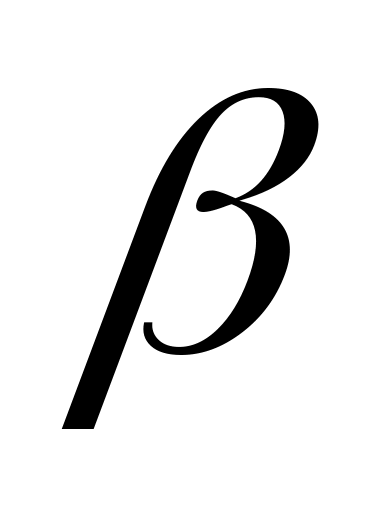 =50°. Найдите диэлектрическую проницаемость среды. Выталкивающей силой пренебречь.
=50°. Найдите диэлектрическую проницаемость среды. Выталкивающей силой пренебречь.
5.5*Оптическая система дает действительное изображение предмета. Можно ли найти такое положение рассеивающей линзы с фокусным расстоянием 1м, при котором изображение остается действительным и станет в три раза больше? Задачу решить построением.
6 Графические задачи
6.1 Изобразите графически силы, с которыми гири 1 и 5кг действуют на подставку.
6.2 Изобразите графически силы 5 и 20Н, действующие на одну и ту же точку тела под углом 450.
6.3 Один мальчик толкает сани сзади с силой 20Н, а второй тянет их за веревку с силой 15Н. Изобразите эти силы графически, считая, что они направлены горизонтально, и найдите их равнодействующую.
6.4 В шахту равноускоренно опускается бадья массой 280кг. За первые 10сек она прошла 35м. Определите натяжение каната.
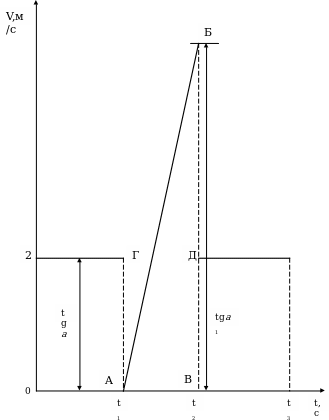
6.5 График скорости имеет вид, изображенный на рисунке (Приложение 8) (t1=2c, t2=4c, t3=6c). Нарисовать график зависимости ускорения от времени. Найдите среднюю скорость в случаях: 1) за первые 4сек; 2) за все время движения. В какие моменты времени мгновенная скорость совпадает со средней скоростью, вычисленной за все время движения?
Приложение 2
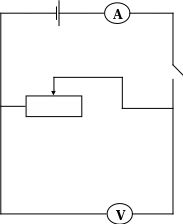
Решение: проведем анализ условия задачи. Амперметр показывает силу тока в цепи, вольтметр-падение напряжения на реостате. При перемещении ползунка реостата влево сопротивление реостата уменьшится, а при перемещении вправо - увеличится. Как же будет меняться падение напряжения на реостате? Ответить на этот вопрос с помощью закона Ома для участка цепи не удается. Действительно, U=IR, но если R, например, увеличится, то I уменьшится. Что происходит с произведением IR, сказать нельзя. В этом случаю нужно пользоваться законом Ома для полной цепи I=E/(R+r), который можно записать также в виде IR+Ir=E.
Так как IR=U - падение напряжения на реостате, то, учитывая, что E=const и r=const, можно заключить следующее.
При перемещении ползунка реостата влево его сопротивление R уменьшается, а сила тока в цепи возрастает. Показания амперметра увеличиваются. Одновременно возрастает и падение напряжения на внутреннем сопротивлении - Ir, а падение напряжения на реостате уменьшится. Показания вольтметра уменьшатся.
При перемещении ползунка реостата вправо R возрастает, сила тока I уменьшается, U увеличивается. Показания амперметра уменьшаются, а вольтметра - увеличиваются.
Правильность ответа легко проверить опытом. При использовании эксперимента рассматриваемая задача будет являться качественной экспериментальной задачей.
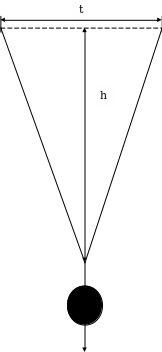
Приложение 3
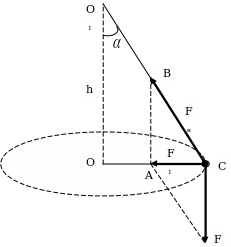
Решение: в избранном нами масштабе изображаем конический маятник (Приложение 3). На гирьку действует сила тяжести F и сила натяжения нити FH. если построить в избранном масштабе конический маятник, то сила F пользуясь масштабом 1 см - 0,2н. Под действием этих сил гирька получает ускорение, направленное к центру окружности. Следовательно, и равнодействующая FI сил F и FH направлена по радиусу к центру. Для построения равнодействующей FI и силы натяжения FH из конца вектора F проводим прямую линию, параллельную нити, до пересечения с радиусом. FI=AC  0,35h. далее из точки А проводим вертикальную прямую до пересечения с нитью. FH=BC
0,35h. далее из точки А проводим вертикальную прямую до пересечения с нитью. FH=BC  1,1 н.
1,1 н.
Решение 2: из подобия треугольников OOIC, ABC и ACF следует:
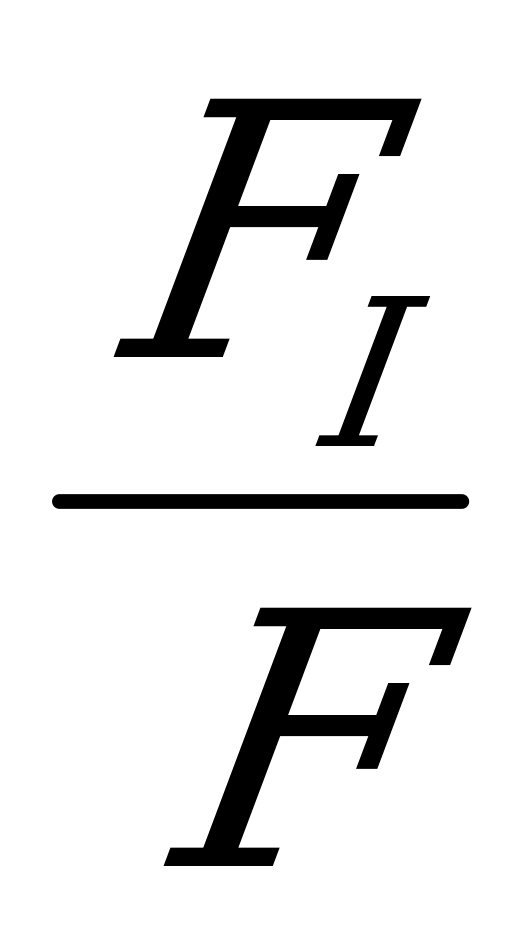 =
= ; FI=
; FI= ; h=
; h=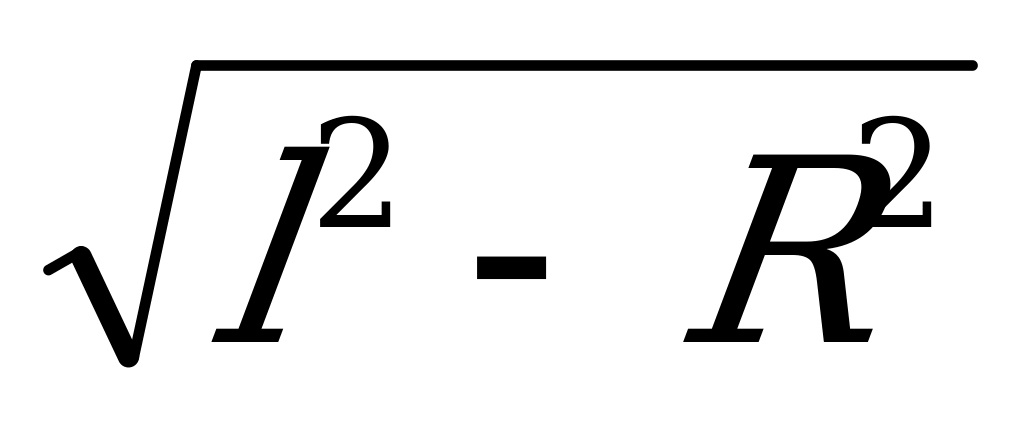
 57 см.
57 см.
FI 36н;
36н; 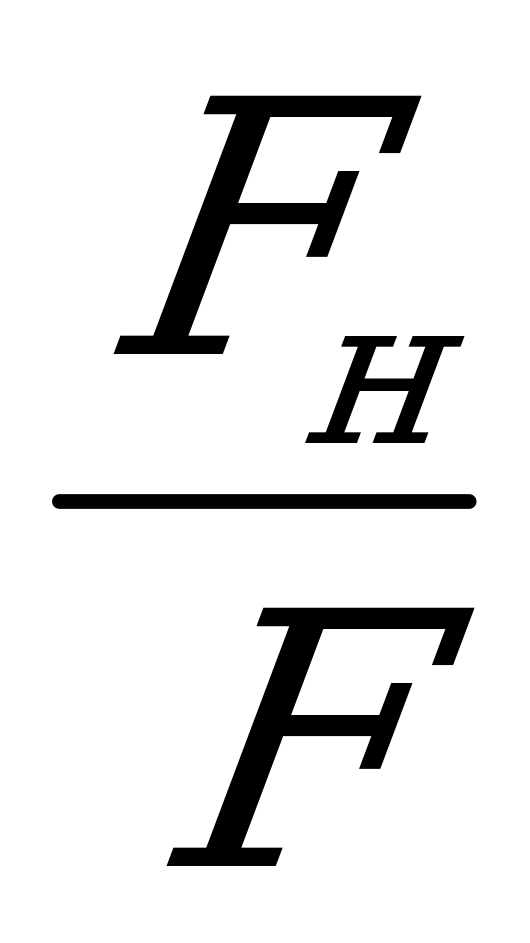 =
=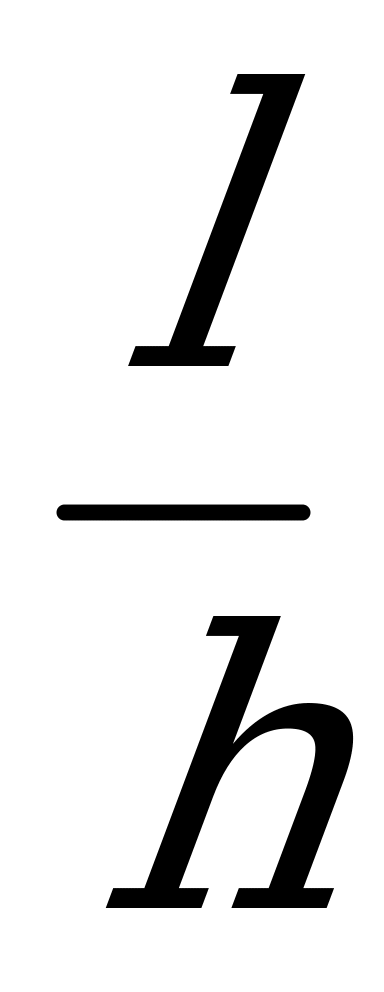 ; Fн
; Fн 1,1н.
1,1н.
Проверка 1. Оттянем гирьку с помощью динамометра от вертикали на 20 см. Сила тяги динамометра и будет численно равна FI.
Проверка 2. Подсчитав число оборотов n гирьки за секунду, найдем силу по формуле F] =4л2п2тR.
Приложение 4
Решение: сделаем чертеж (Приложение 4). Силу тяжести F разложим на две составляющие F1 и F2, направленные вдоль частей троса (Приложение 5). Нетрудно доказать, что F1=F2, MN=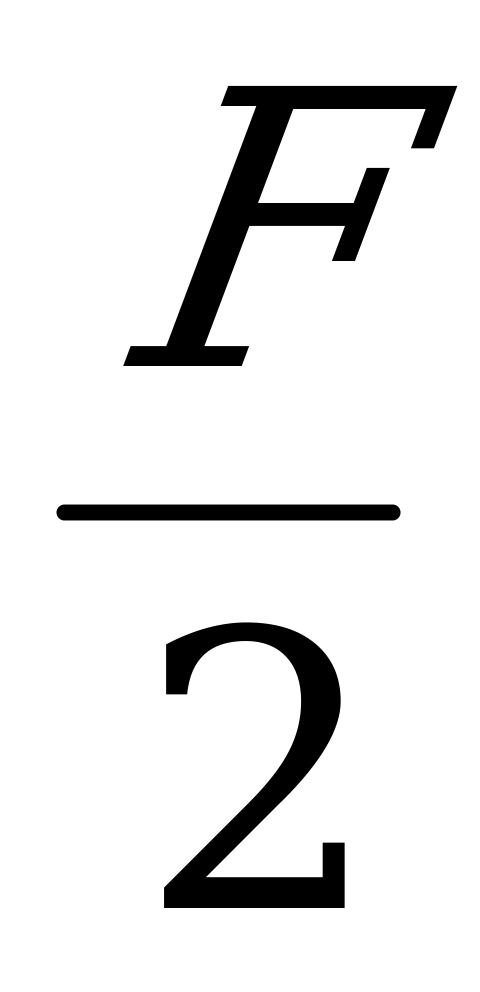 и
и  OMB
OMB
 MNF1. Из подобия треугольника следует: -
MNF1. Из подобия треугольника следует: - 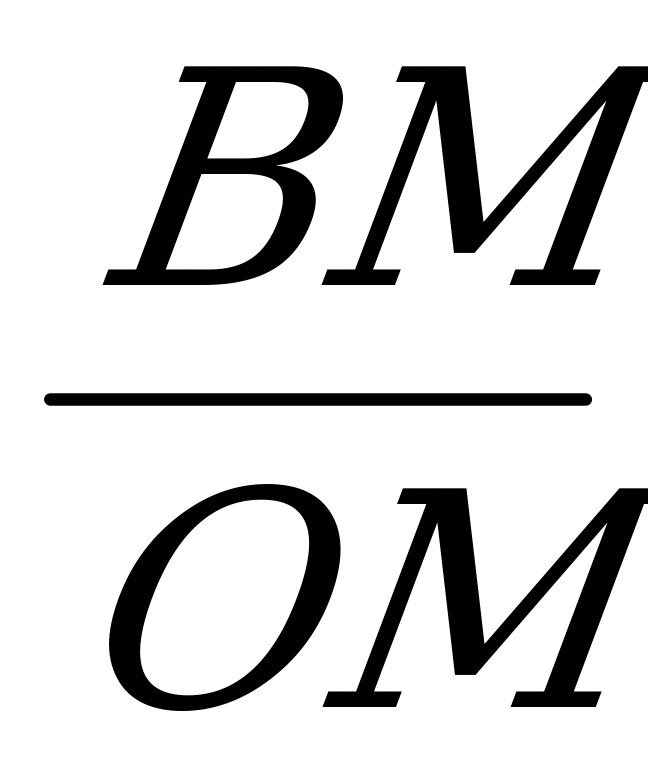 =
=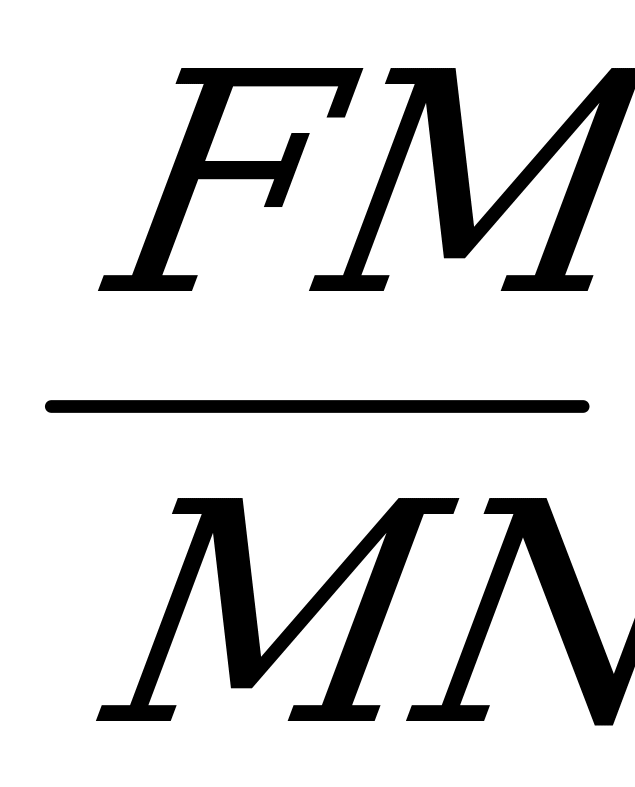 . Так как стрела прогиба невелика, примем, что МВ=
. Так как стрела прогиба невелика, примем, что МВ=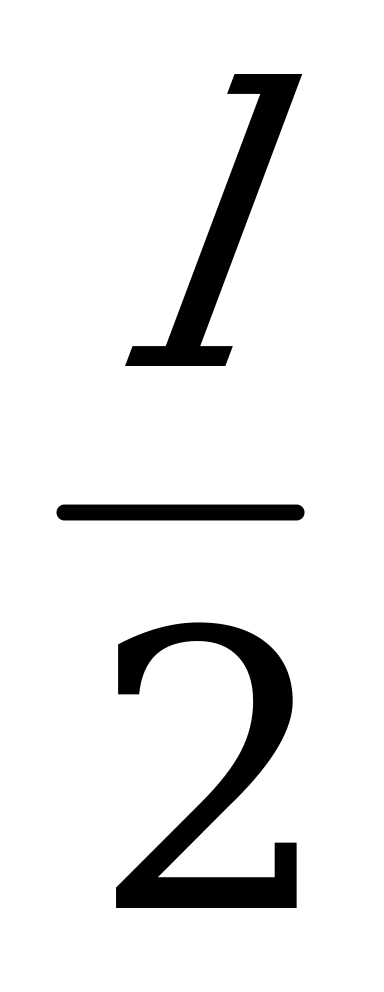 , тогда
, тогда 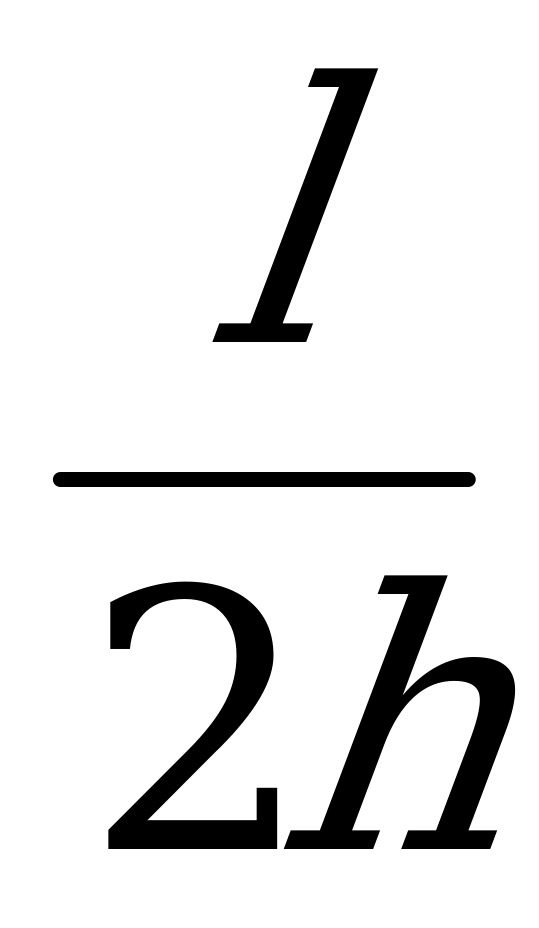 =
=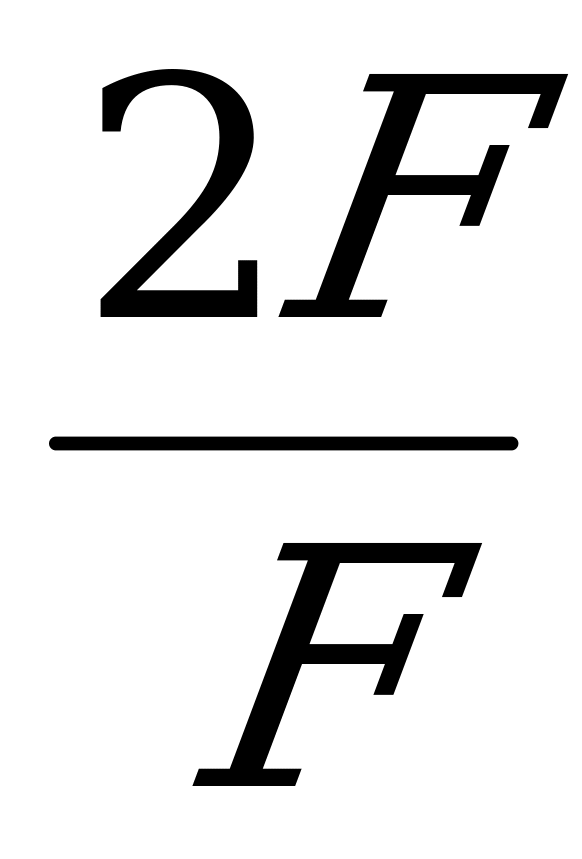 . Отсюда F1=
. Отсюда F1=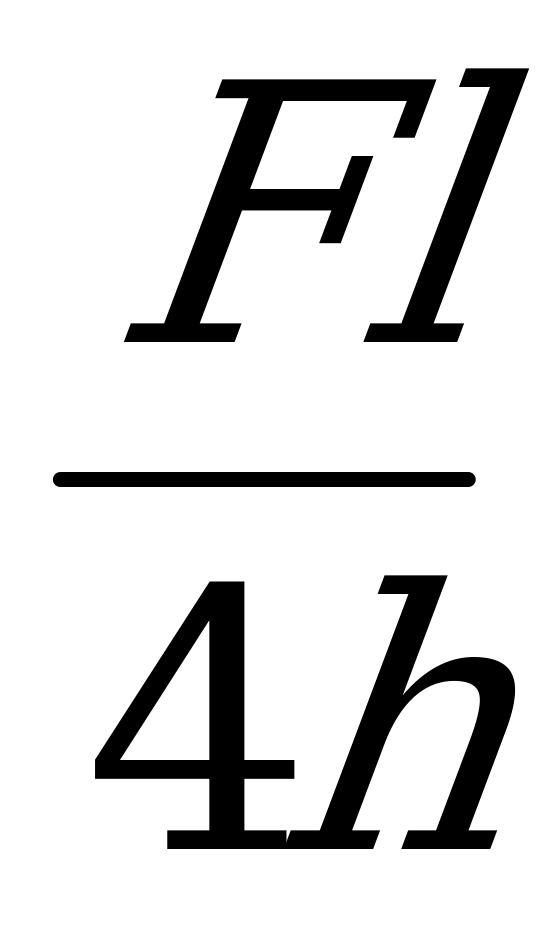 =
=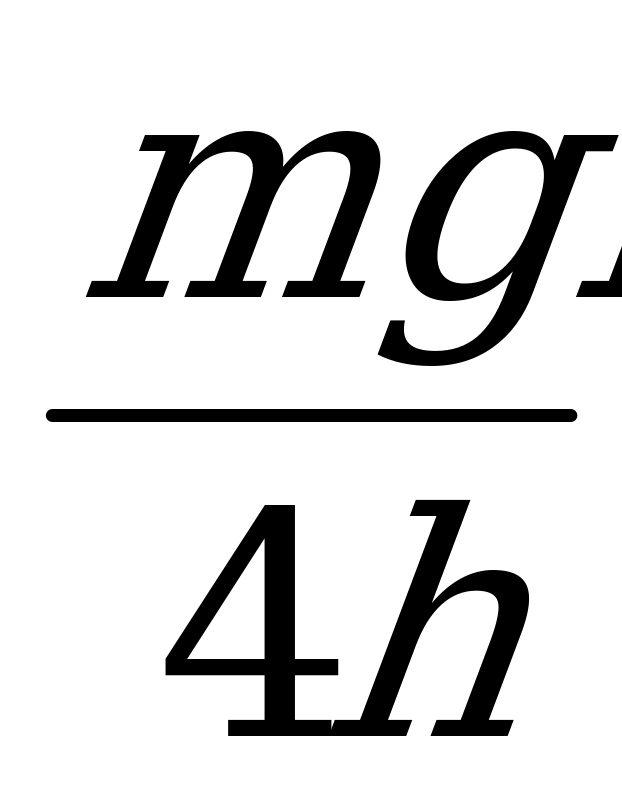 =
=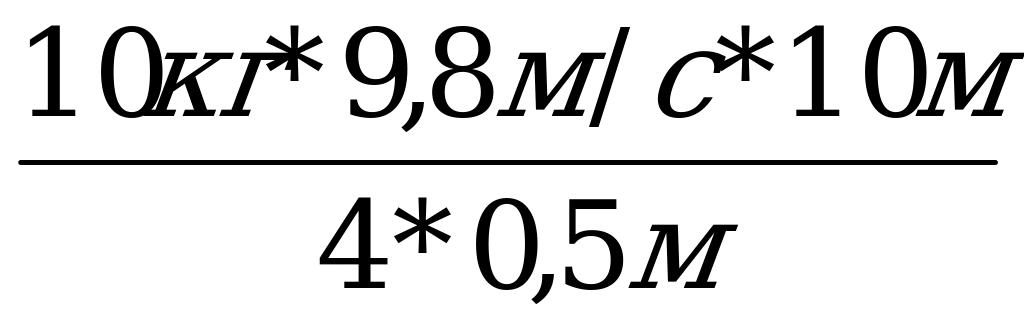 =490н.
=490н.
Искомое натяжение троса равно по величине и противоположно по направлению силе F.
В случае геометрического метода решения задач можно использовать не только геометрические соотношения, но и тригонометрические формулы.
Приложение 5
Приложение 6
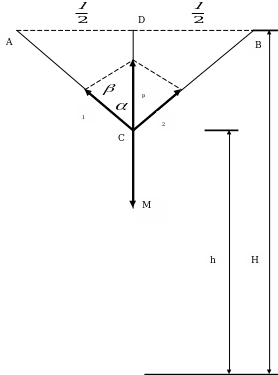
Решение: Фонарь будет находится в равновесии при условии:
O= p+ M
p+ M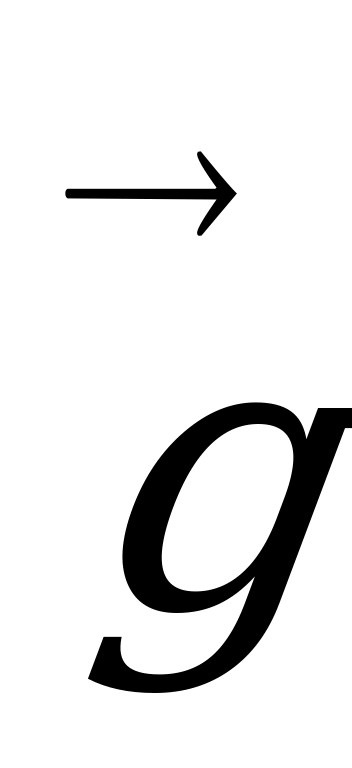 , где
, где 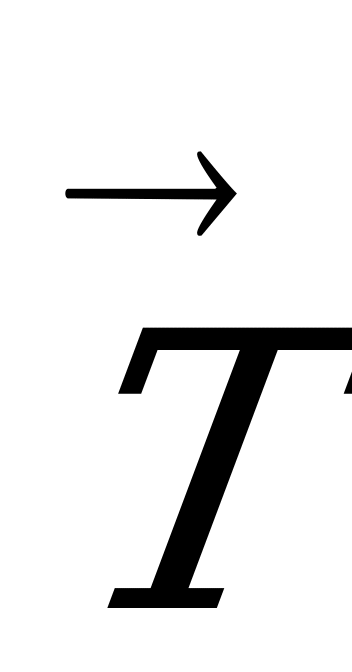 р=
р=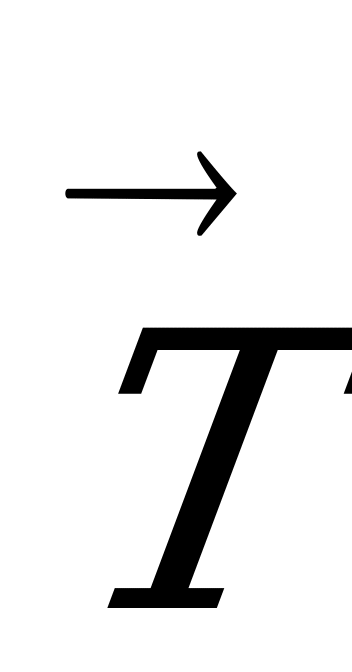 1+
1+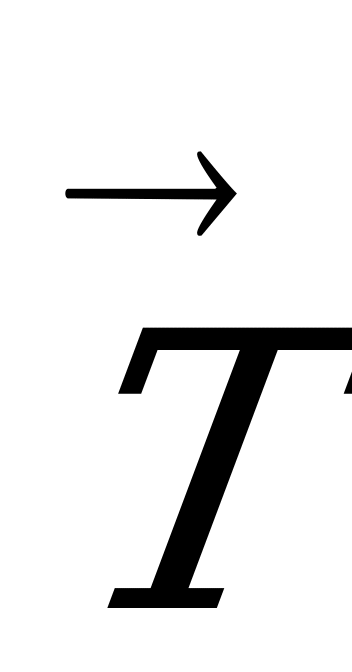 2 - равнодействующая сил натяжения
2 - равнодействующая сил натяжения  1 и
1 и  2.
2.
T1=T2=T (канат невесом).
Пусть а=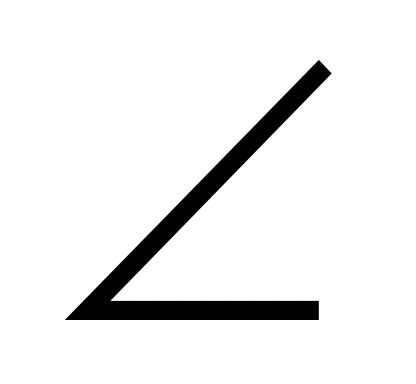 ACD (
ACD ( ACD), тогда
ACD), тогда 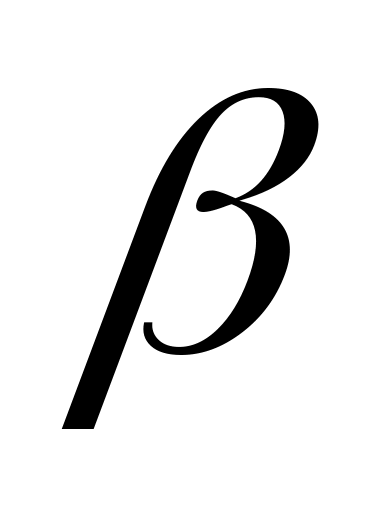 =
= - 2
- 2 ;
; 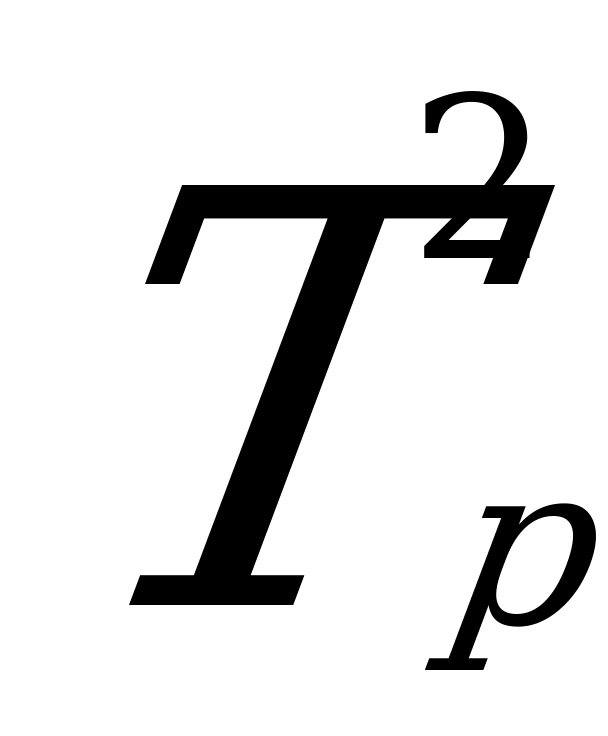 =
=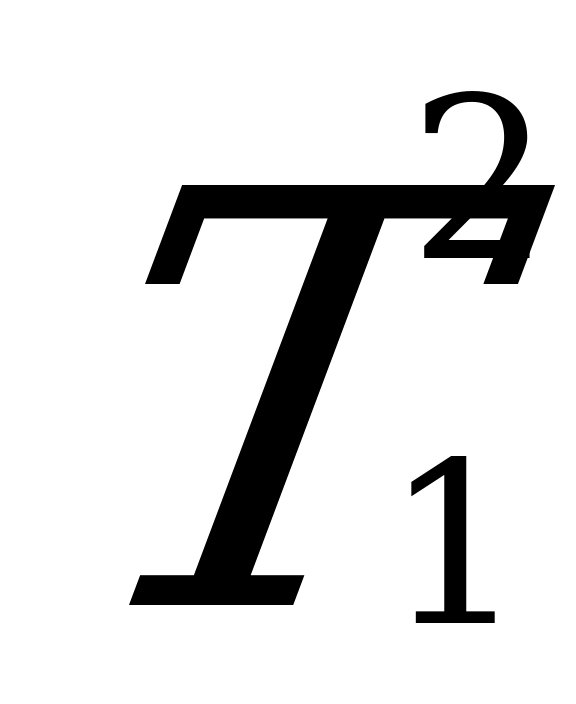 +
+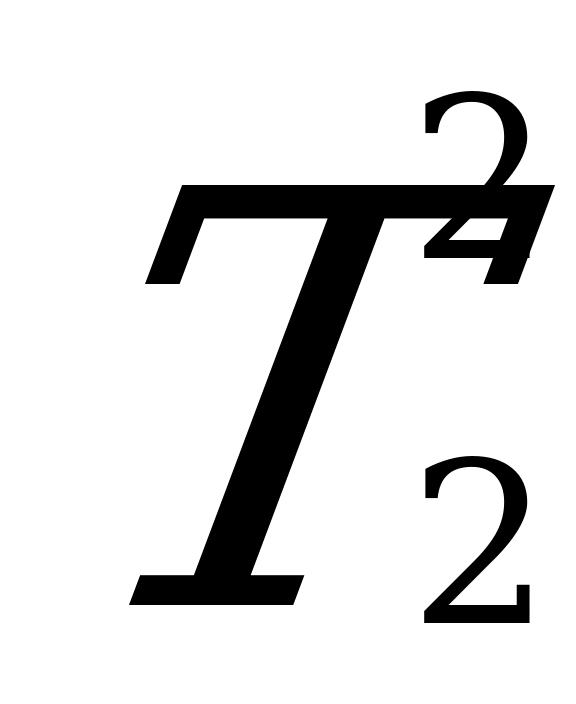 -
- 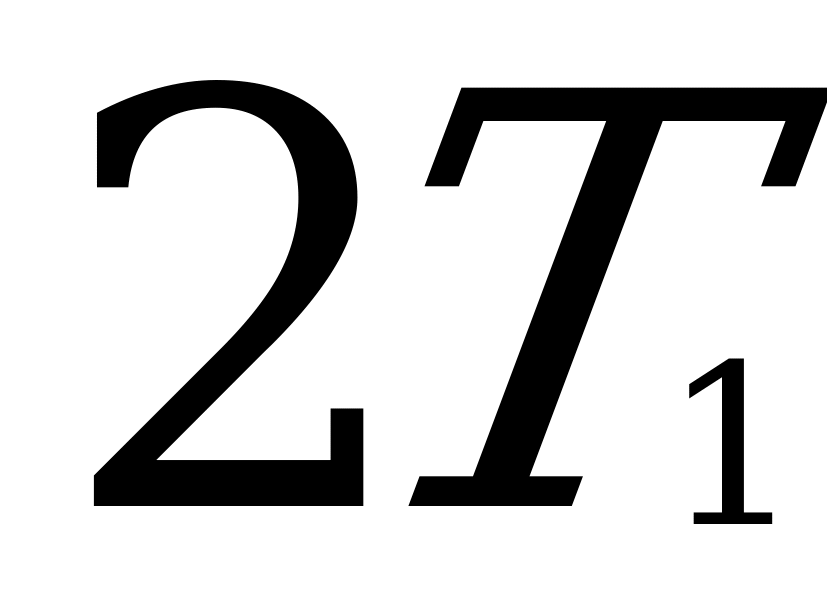
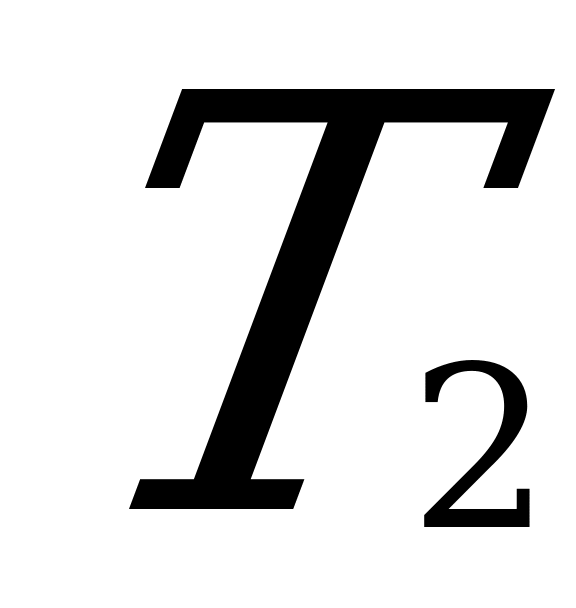 cos
cos 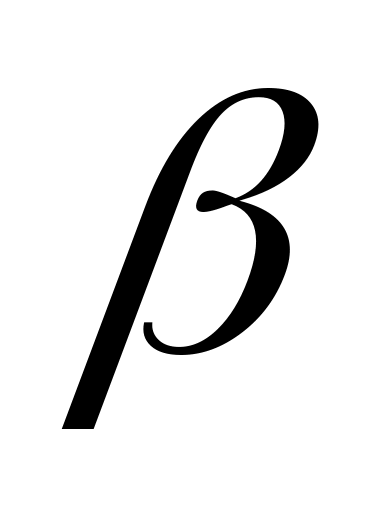
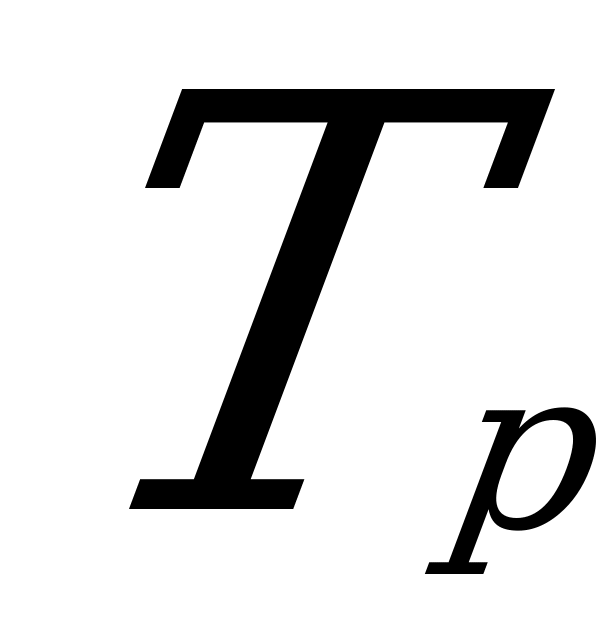 =
=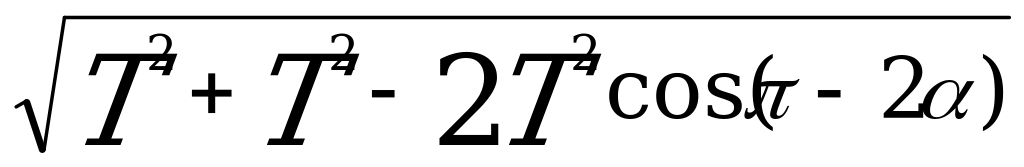 - модуль силы
- модуль силы  p
p
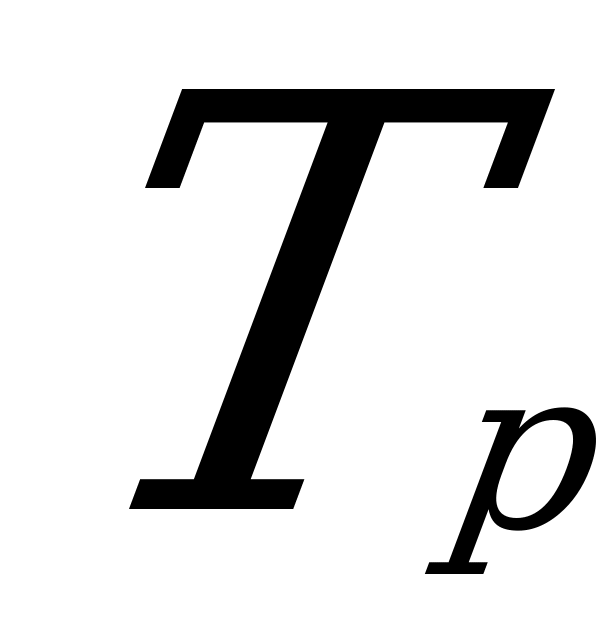 =
=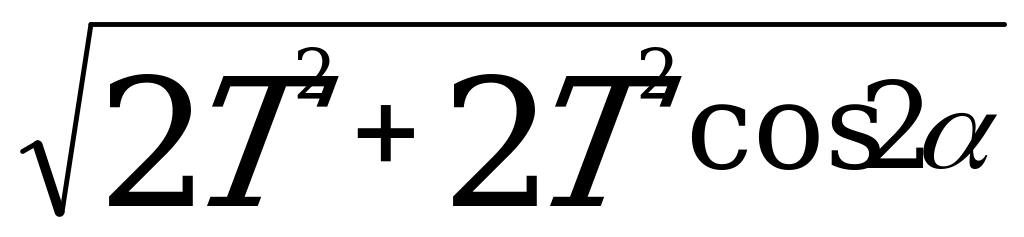 +
+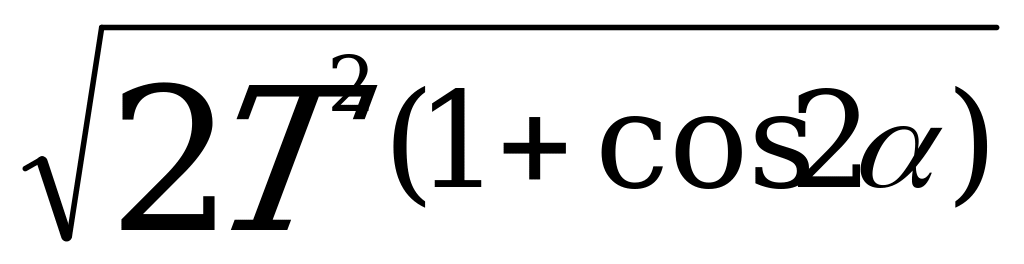 (cos(
(cos( -2
-2 )=-cos 2
)=-cos 2 )
)
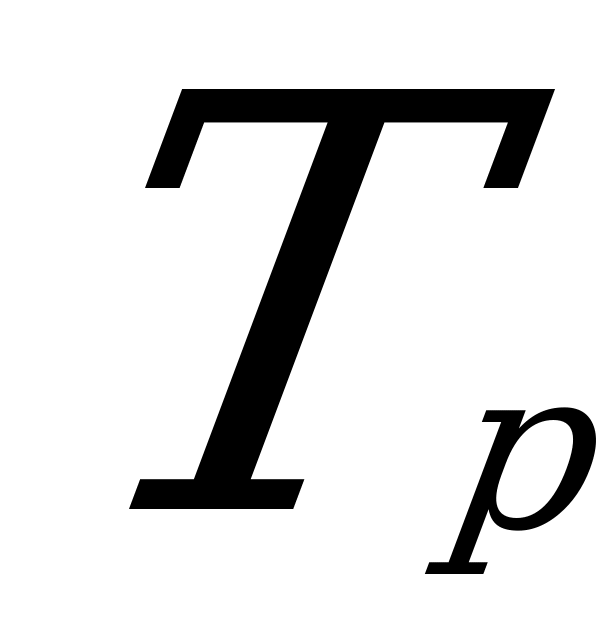 =
=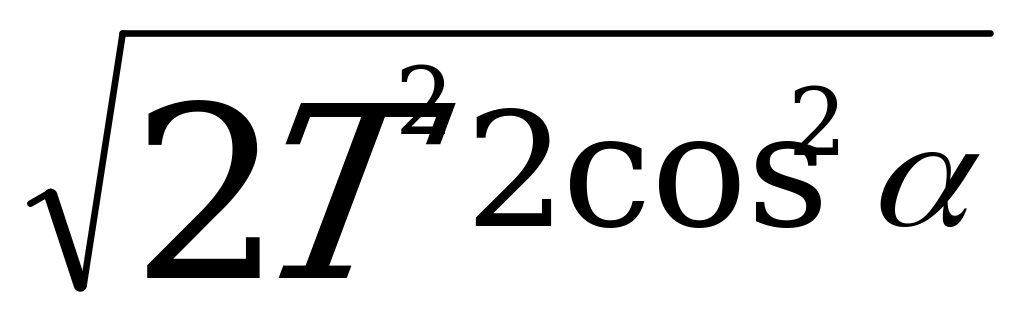 =2Tcos
=2Tcos (1+cos2
(1+cos2 =2cos2)
=2cos2)
cos  =
=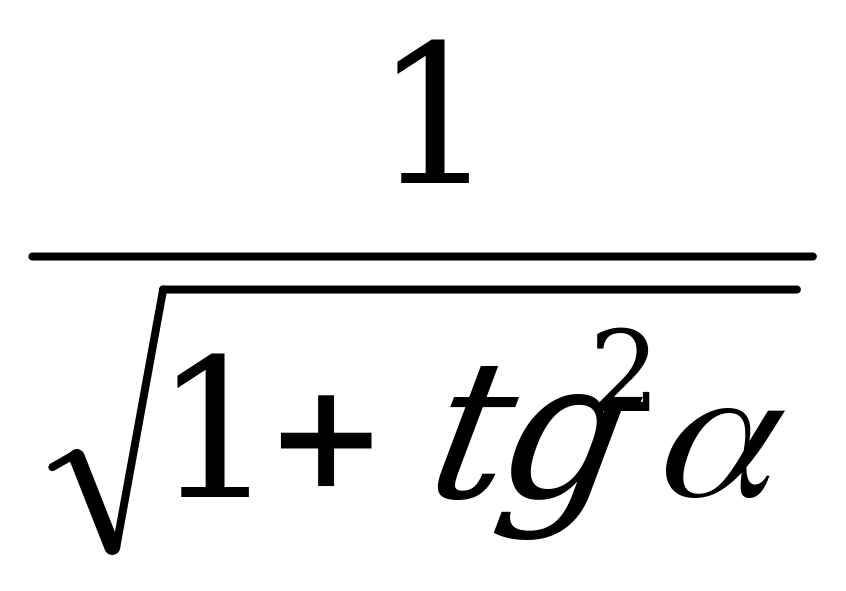 (1+tg2
(1+tg2 =
=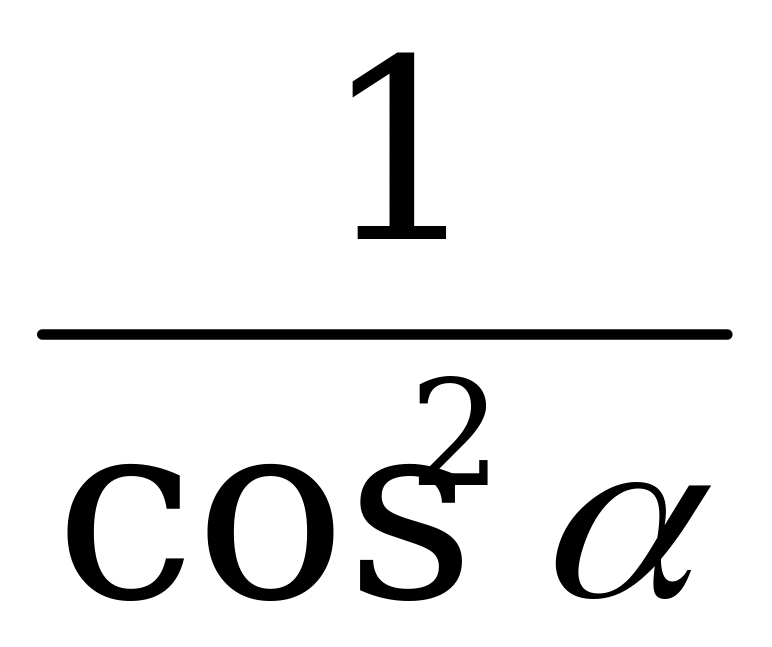 )
)
tg =
=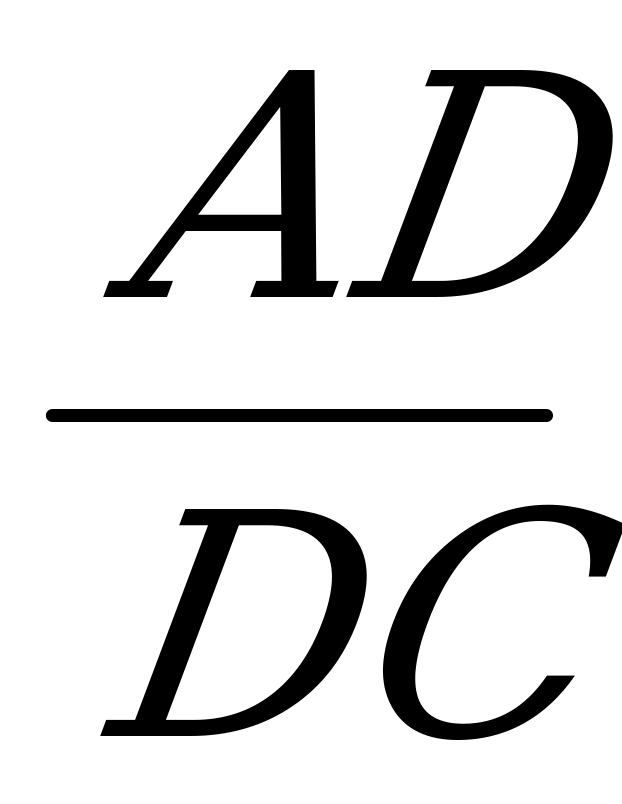 (
( ACD); AD=
ACD); AD=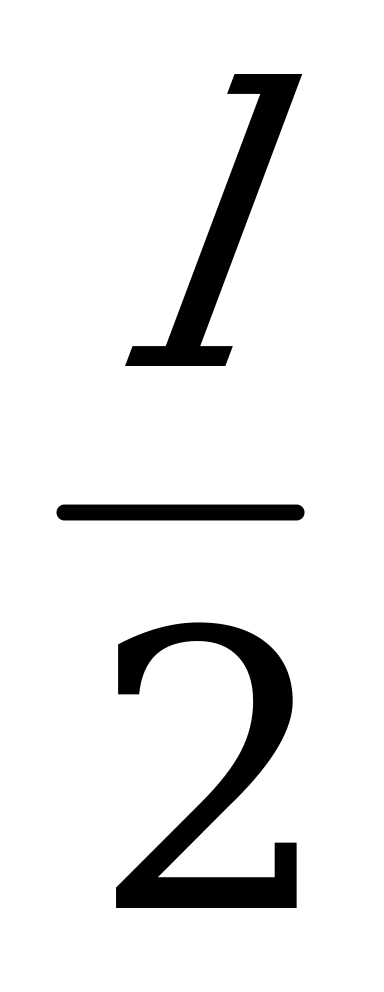 ; DC=H-h
; DC=H-h
tg =
=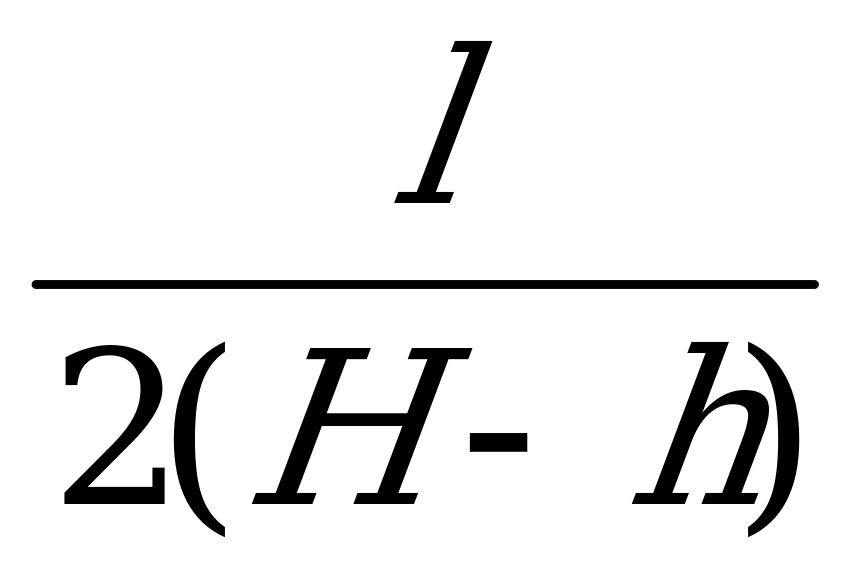 ; cos
; cos  =
=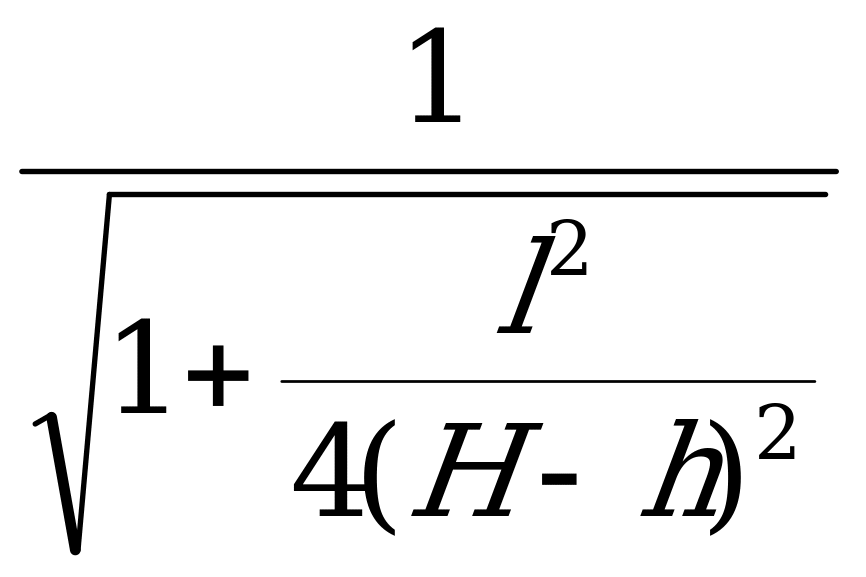 =
=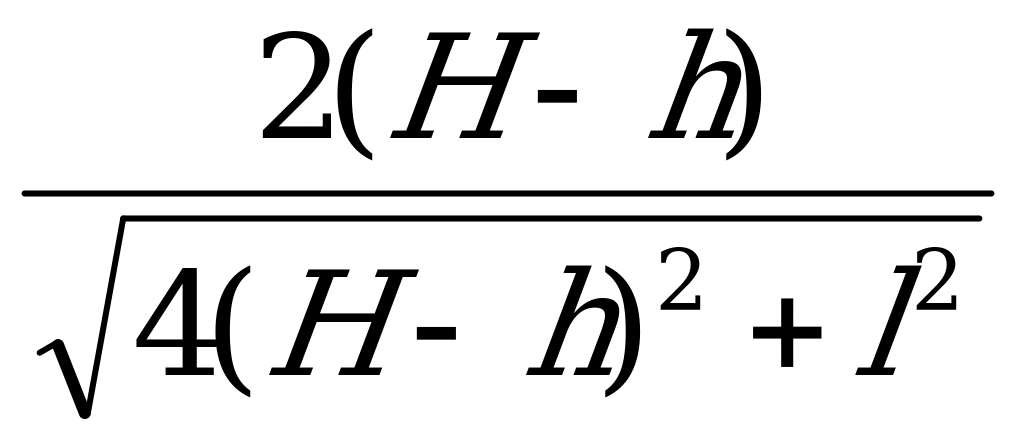
Из условия равновесия фонаря следует:
 p=- M
p=- M ; Tp=Mg
; Tp=Mg
Тогда
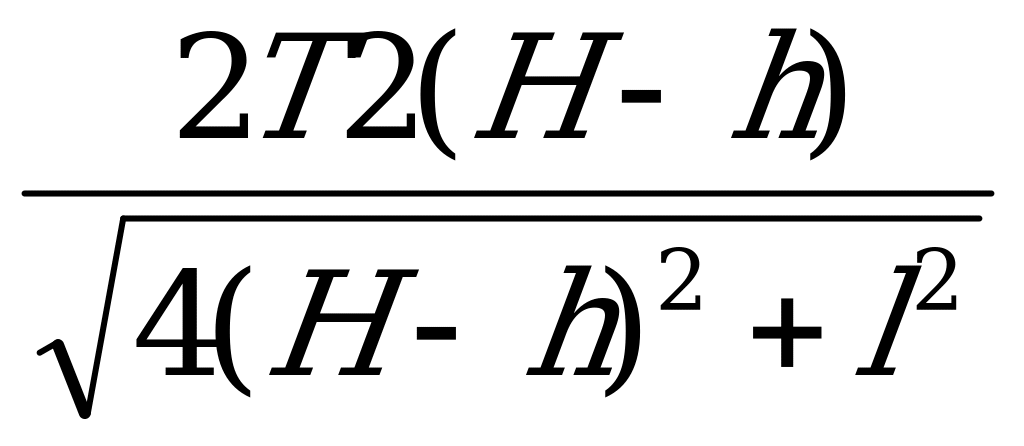 =Mg;
=Mg; 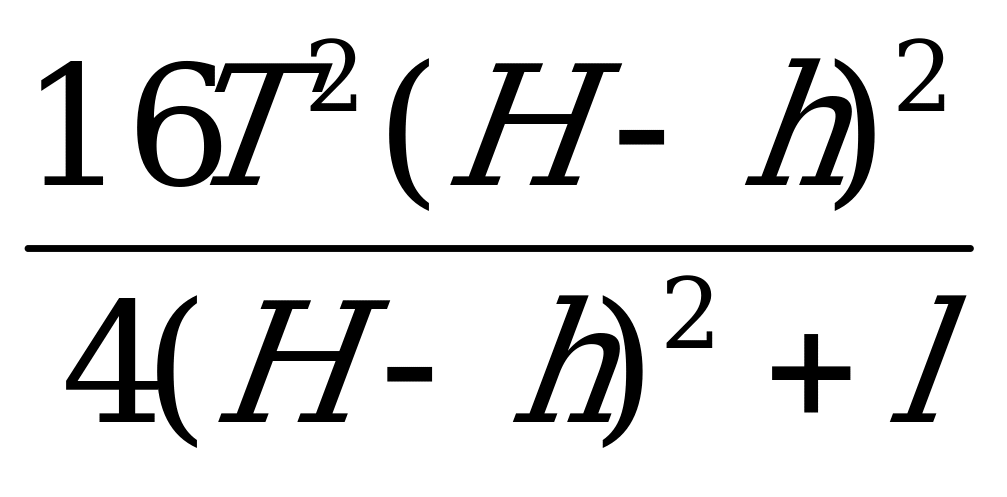 =M2g2
=M2g2
16T2(H-h)2=4(H-h)2M2g2+l2M2g2
(16T2-4M2g2)(H-h)2=l2M2g2
4(4T2-M2g2)(H-h)2= l2M2g2
(H-h)2=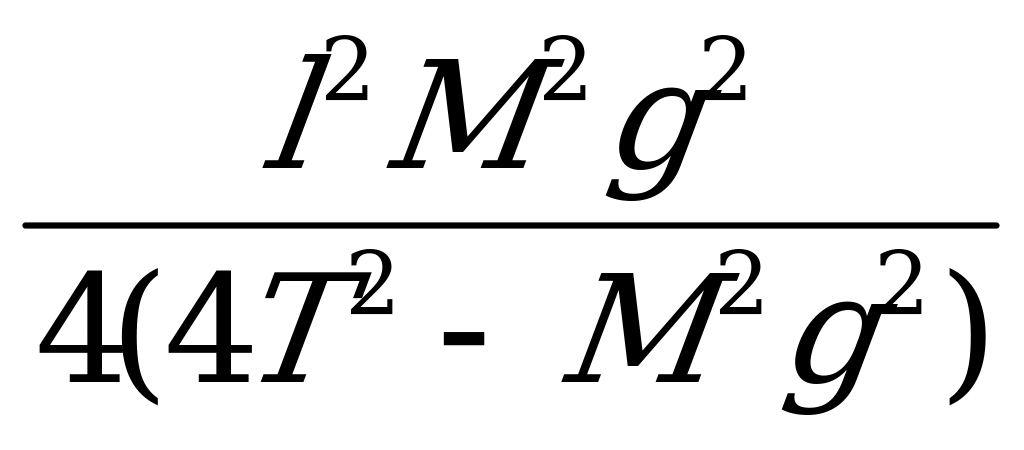 ; H-h=
; H-h=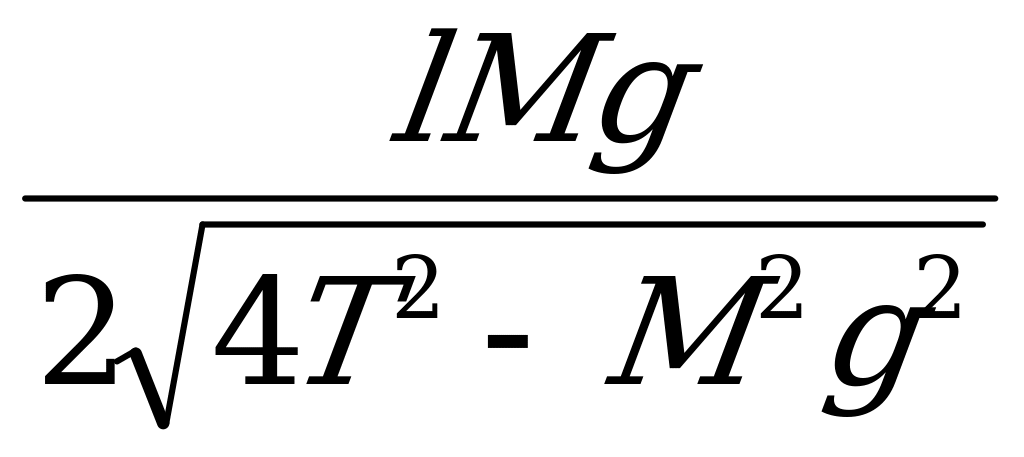
H=h+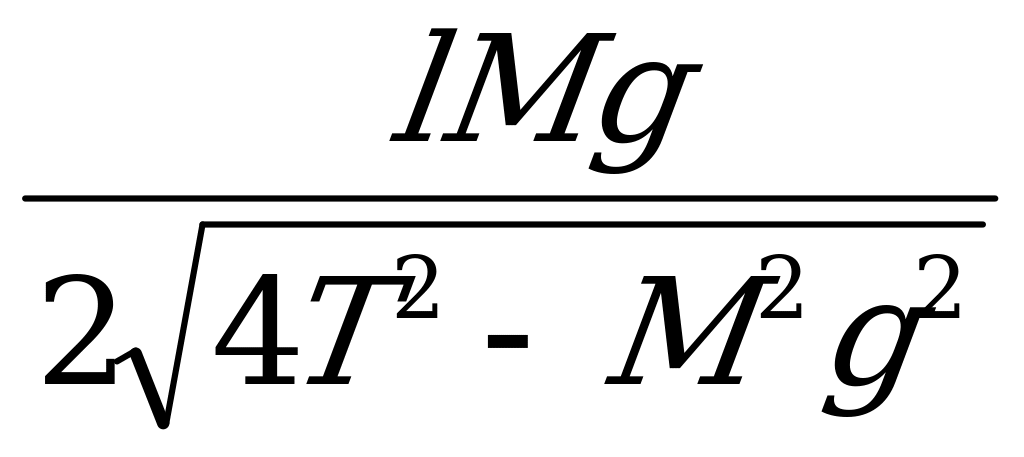 - высота крепления концов каната.
- высота крепления концов каната.
H=5+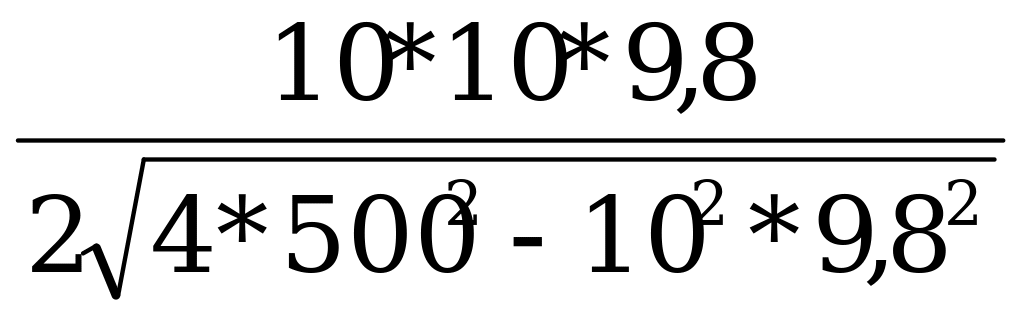 =5,49 (м)
=5,49 (м)
Ответ: 5,49 м.
Приложение 7
Приложение 8
Приложение 9
Приложение 10
44









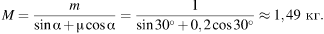 Заключение
Заключение 




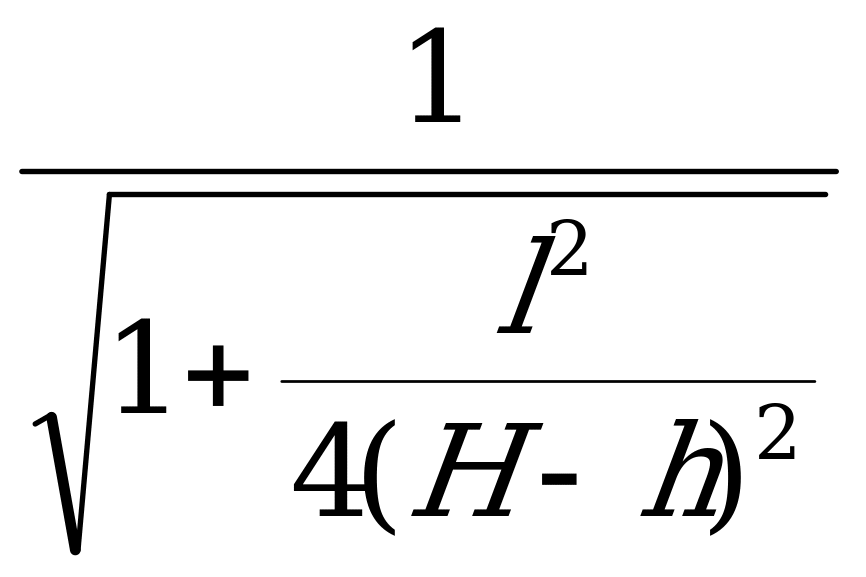 =
=













