Приложение 1
Теоретический материал
Основные понятия систем счисления
Для записей результатов количественных (числовых) измерений используются числа. Число – это основное понятие математики, используемое для количественной характеристики, сравнения и нумерации объектов. Письменными знаками (символами) для записи чисел служат цифры. Самыми распространёнными цифрами являются арабские цифры, представляемые знаками от нуля (0) до девяти (9); менее распространены римские цифры. Обычно количество цифр (символов) для записи чисел ограничено, поэтому для больших чисел цифры в его записи будут повторяться. Конечный набор (множество) цифр (символов) называется алфавитом. Совокупность приемов и правил изображения чисел цифровыми знаками называется системой счисления.
Система счисления должна обеспечивать:
возможность представления любого числа в заданном диапазоне;
однозначность, сжатость записи числа и простоту выполнения арифметических операций;
достижение высокого быстродействия машины в процессе обработки информации.
Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления.
Основание системы счисления также определяет, во сколько раз различаются значения одинаковых цифр в соседних позициях числа. Основание системы счисления записывается справа от числа в нижнем индексе: 510; 1110102; АF17C16 и т.д. Запись числа в некоторой системе счисления называется его кодом.
Все системы счисления можно разделить на 3 вида:
позиционные системы счисления;
непозиционные системы счисления;
смешанные системы счисления.
Позиционные системы счисления
Позиционная система счисления – это система счисления, в которой значение символа зависит от его позиции в ряду цифр, изображающих число, т.е. количественное значение цифры зависит от того, какую позицию в числе она занимает. Классическим примером позиционной системы счисления является десятичная система счисления.
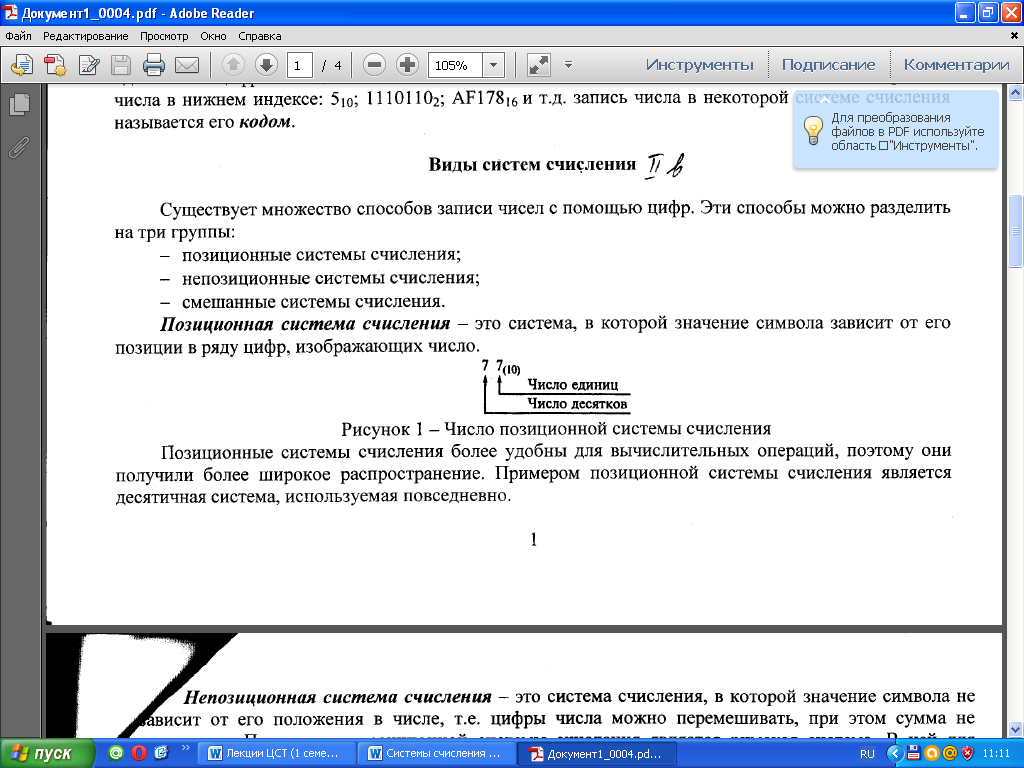
Рисунок 1.1 – Число позиционной системы счисления
Позиционную систему счисления с основанием P принято называть P-ичной. Основание позиционной системы счисления показывает, сколько чисел в алфавите системы счисления, а также определяет, во сколько раз различаются значения одинаковых цифр в соседних позициях числа.
Позиционные системы счисления более удобны для вычислительных операций, поэтому они получили наибольшее распространение.
Примерами позиционной системы счисления также могут служить двоичная, троичная, восьмеричная, шестнадцатеричная и т.д.
Непозиционные системы счисления
Непозиционная система счисления – это система счисления, в которой значение символа не зависит от его положения в числе.
Примером непозиционной системы счисления является унарная (единичная) система счисления. Основное ее применение – обучение детей счету. В ее алфавит входит единственная цифра – 1, а количество единиц соответствует количеству объектов. Так, число 111 в унарной системе счисления обозначает число 3 в десятичной. В числе 111 встречаются три цифры 1, и каждая из них обозначает одну величину – число «один».
Еще одним классическим примером непозиционной системы счисления является римская система счисления, в которой для записи чисел используются буквы латинского алфавита: I – 1,V – 5, X – 10, L – 50, C – 100, D – 500, M – 1000.

Рисунок 1.2 – Число непозиционной системы счисления
При записи чисел в римской системе счисления число составляется по следующим правилам:
если меньшая цифра стоит слева от большей, то меньшая цифра вычитается из большей;
если меньшая цифра стоит справа от большей, то обе цифры складываются. Одинаковые цифры так же складываются.
Примеры:
IX = 9.
MMXI = 1000 + 1000 +10 + 1 = 2011.
MCMXCVIII = 1000 +(-100 + 1000) + (-10 + 100) + 5 + 1 + 1 + 1 = 1999.
Правила перевода из одной системы счисления в другую
В двоичной системе счисления все числа записываются с помощью двух цифр 0 или 1, основание (базис) двоичной системы счисления q=2.
В восьмеричной системе счисления все числа записываются с помощью восьми цифр 0, 1, 2, 3, 4, 5, 6, 7, основание восьмеричной системы счисления q=8.
В десятичной системе счисления все числа записываются с помощью десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В шестнадцатеричной системе счисления все числа записываются с помощью шестнадцати цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A (количественный эквивалент числа 10), B (11), C (12), D(13), E (14), F (15), базис шестнадцатеричной системы счисления q=16.
| Для того чтобы перевести целую часть числа из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную, необходимо: 1. Последовательно делить данное число и получаемые при делении целые частные на основание q новой системы счисления (2, 8 или 16), выражая промежуточный результат цифрами исходной системы, до тех пор, пока частное не станет равным нулю. 2. Полученные остатки, фактически являющиеся цифровым выражением числа в новой системе, привести в соответствие с алфавитом этой системы счисления (имеются в виду системы счисления с основанием больше 10). 3. Записать число в новой системе счисления, начиная с последнего остатка. |
Пример 1. Перевести число 2310 в двоичную систему счисления. | _23 |
| 2 |
|
|
|
|
|
|
|
| | 22 |
| _11 |
| 2 |
|
|
|
|
|
| |  |
| 10 |
| _5 |
| 2 |
|
|
|
| |
|
| |
| 4 |
| _2 |
| 2 |
|
| |
|
|
|
| |
| 2 |
| 1 |
|
| |
|
|
|
|
|
| |
|
|
|
| |
|
|
|
|
|
|
|
| |
|
| |
|
|
|
|
|
|
|
|
|
|
| Получаем 2310=101112 |
При переводе чисел из системы счисления с основанием q в десятичную систему счисления необходимо пронумеровать разряды целой части справа налево, начиная с нулевого, и дробной части, начиная с разряда сразу после запятой, слева направо – начальный номер -1. Затем вычислить сумму произведений соответствующих значений разрядов на основание q системы счисления в степени, равной номеру разряда
Пример 3. Перевести число 10110110111,1012 в десятичную систему счисления
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1, | 1 | 0 | 12=1*29+0*28+1*27+1*26+0*25+1*24+1*23+0*22+1*21+ |
+1*20+1*2-1+0+2-2+1*2-3= =512+0+128+64+0+16+8+0+2+1+0,5+0+0,125=731,62510


















