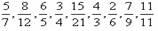Открытый урок математики в 6 классе по теме: "Умножение дробей"
Цель урока: организация деятельности учащихся по изучению и закреплению понятия и навыков умножения обыкновенной дроби на натуральное число.
Задачи
Обучающие:
- сформировать понятие умножения дроби на натуральное число;
- отработать навык умножения дроби на натуральное число.
Развивающие:
- развивать интерес к предмету;
- развивать умение концентрироваться, память, внимание, логическое мышление, воображение, умение сопоставлять, делать выводы, умение переносить знания в новые ситуации;
- развивать умение слушать, работать, самостоятельность, развивать математическую речь.
Воспитательные:
- формировать культуру общения и коммуникативных умений, учащихся при работе учащихся самостоятельно, в группе;
- воспитывать познавательный интерес к предмету;
- побуждать учеников к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.
Оборудование: компьютер, мультимедийный проектор и экран или интерактивная доска; презентация у к уроку; учебник математики 6 класса (автор Н.Л. Виленкин); раздаточный материал с заданиями для работы по группам.
Тип урока: урок изучения нового материала.
Методы организации учебной деятельности:
- проблемный,
- частично-поисковый;
- исследовательский,
- наглядный,
- словесный.
Формы обучения:
- работа в группах (в ходе открытия новых знаний);
- фронтальная работа (в ходе устного счета);
- индивидуальная работа (в ходе закрепления изученного материала);
- работа в парах (при взаимопроверке).
Формы организации учебной деятельности:
- опрос по цепочке в ходе устного счета;
- игра «Точка зрения»;
- взаимопроверка.
Панируемые результаты: в ходе урок учащиеся смогут:
- самостоятельно сформулировать правило умножения обыкновенной дроби на натуральное число;
- применить правило при решении упражнений.
По завершении урока учащийся должен:
знать правило умножения обыкновенной дроби на натуральное число;
уметь умножать обыкновенную дробь на натуральное число.
Ход урока:
I. Орг.момент (Подготовка к активной учебно-познавательной деятельности - 2 мин)
Здравствуйте, ребята! Я рада приветствовать Вас на уроке математики. Сегодня мы с вами отправимся в путь за знаниями. В дорогу мы возьмем только самое необходимое: хорошее настроение и наши знания.
Каждый наш урок мы проведем под девизом.
Чтобы переварить знания, надо поглощать их с аппетитом. (А. Франц).
Как Вы понимаете эти слова? (ответы)
Мы будем мыслить, рассуждать, исследовать и, думаю, с удовольствием получать новые знания по математике. А какой раздел математики мы изучаем сейчас? (Изучаем тему «Обыкновенные дроби», действия с обыкновенными дробями)
Что из этого раздела мы уже знаем и умеем? (Умеем складывать, вычитать, сравнивать дроби с одинаковыми, разными знаменателями)
II. Актуализация знаний (мотивация на учебную деятельность, повторение материала, создание проблемной ситуации)
Задание1:
1. Разбей дроби на группы, укажи признак разбиения:
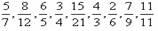
Дополнительные вопросы:
Назови правильные дроби.
Назови неправильные дроби.
Выдели целую и дробную части из неправильной дроби.
Какие дроби называются неправильными?
Возможные ответы: Правильные; неправильные. Сократимые; несократимые.
2.Что значит сократить дробь?
Задание 2 (работа в группе) Сократите дроби и установите соответствие между названием и изображением редких цветковых растений, внесенных в Красную книгу.
| 
| Фиалка наскальная |
| 
| 
|
| 
| Стерис альпийский |
| 
| 
|
| 
| Родиола розовая |
| 
| 
|
| 
| Купальница открытая |
| 
| 
|
| 
| Мак полярный |
| 
| 
|
| 
| Минуарция крупноплодная |
| 
| 
|
| 
| Мытник прелестный |
| 
| 
|
| 
| Пион уклоняющийся |
| 
| 
|
3. Замените сумму произведением. а) 2+2+2+2+2+2 б) a+ a + a + a
4. Замените произведение суммой. а) 6 ∙ 2 в) b ∙ 3
5. Найдите площадь прямоугольника со сторонами 3м и 4м (12м2)
Задача 1 [2]. Жили-были лиса да заяц. У лисицы была избёнка ледяная, а у зайчика лубяная; пришла весна красна - у лисицы избушка растаяла, а у зайчика стоит по-старому. Лиса попросилась у зайчика погреться, да зайчика-то и выгнала.
Решила лиса сделать евроремонт, постелить линолеум. А для этого ей надо найти площадь пола, если известно, что ширина пола 4/5 м, а длина 3 м.
Вопросы:
О чем говориться в задаче?
С какими величинами эта задача?
Какие величины известны?
Что надо найти?
Как найти площадь?
Какое выражение можно составить для решения задачи?
Ответ: 4/5 * 3.
П рочитайте задачу 2
Задача 2. Черепаха за 1 мин проползает м.
Какое расстояние она преодолеет за 4 мин.?
Вопросы:
О чем говориться в задаче?
С какими величинами эта задача?
Какие величины известны?
Что надо найти?
Как найти расстояние?
Какое выражение можно составить для решения задачи?
Ответ: 2/9 * 4.
III Сообщение темы урока. Целеполагание.
Учитель записывает эти выражения на доске: 4/5 * 3; 2/9 * 4.
Вопрос: Сможем ли мы найти значения этих выражений? Ответ: Нет.
(Возможен ответ , гипотезу записать на доске, проверить решение в конце урока).
Вопрос: Каких знаний нам не хватает? Ответ: Мы не умеем умножать обыкновенную дробь на натуральное число.
Сформулируйте, пожалуйста, тему урока. Ответ:.
Откройте тетради, запишите число и тему урока: .
Вопрос: Как вы думаете, чему мы должны научится на уроке?
Цель: Сегодня на уроке мы должны самостоятельно сформулировать правило умножения обыкновенной дроби на натуральное число и применить правило при решении упражнений.
Историческая справка. (сообщение обучающегося)
Слово в русском языке появилась в 8 веке и происходит это слово от глаголов , . При разделе добычи, при измерении величин люди встречались с необходимостью ввести числа - обыкновенные дроби. Действия над дробями еще в среднем веке считались самой сложной областью математики. Умение оперировать дробями в Древнем Риме воспринималось как чудо. Люди, знающие дроби, пользовались особым почётом и уважением. Римский оратор и писатель Цицерон говорил, что без знаний дробей никто не может признаваться знающим арифметику.
До сих пор у немцев сохранилась такая поговорка .
Ответ: так говорят про человека, попавшего в затруднительную ситуацию, что он попал в дроби. Это означает: попасть в тяжёлое, трудное положение
IV Изучение нового материала.
Как найти значение выражения 4/5*3? Скажите вашу точку зрения (игра ).
У вас на партах раздаточный материал
Первая ряд находит значение выражения первым способом, второй - вторым, третий- третьим способом.
| Задание: Выполните умножение 4/5 * 3 по указанному алгоритму |
| 1 ряд | 2 ряд | 3 ряд |
| 1.Выразите метры в сантиметрах и найдите значение выражения 2. Полученный результат запишите в квадратных метрах. 3. Запишите полученный результат в виде обыкновенной дроби (если надо сократите дробь). | 1. Замените действие умножение действием сложения трех слагаемых, каждый из которых равен 4/5. 2. Выполните сложение (если нужно сократите дробь). 3. Запишите результат в виде обыкновенной дроби или смешанного числа. | 1. Запишите обыкновенную дробь в виде десятичной дроби. 2. Выполните умножение десятичной дроби на натуральное число. 3. Запишите полученную десятичную дробь в виде обыкновенной дроби. |
| 4.Сформулируйте правило умножения обыкновенной дроби на натуральное число. |
Учащиеся выдвигают свои гипотезы нахождения значения выражения.
Практическая работа учащихся в парах с раздаточным материалом. Учащееся каждой колонки выполняет свое задание, заполняют раздаточные листы.
Один учащийся от ряда представляет отчет о проделанной работе на доске.
Учащиеся слушают и проверяют свое решение.
Вопрос: Давайте, сравним решения и попробуем выбрать наиболее рациональный способ
Учащиеся обсуждают решения и делают выводы.
Возможные выводы учащихся:
1. Обыкновенные дроби не были бы никому нужны, если бы для вычислений их сначала нужно было бы перевести в десятичные дроби, а затем снова вернуться к обыкновенным дробям.
2. Обыкновенные дроби не были бы никому нужны, если бы для вычислений их сначала нужно было бы перевести в другие более мелкие единицы измерения (массы, площади, длины и т.д.), а затем снова вернуться к обыкновенным дробям.
3. Обыкновенные дроби не были бы никому нужны, если бы для вычислений их сначала нужно было бы умножение заменить сложением, а затем снова вернуться к обыкновенным дробям.
Сравните: 4/5* 3 и 12/5.
Что интересного заметили?
Проверить гипотезы, которые учащиеся выдвигали в начале урока (если они были).
Вернемся к задаче 2. Черепаха за 1 мин проползает 2/9 см. Какое расстояние она преодолеет за 4 мин?
Вопрос: сейчас мы можем ответить на вопрос задачи 2? Сделайте запись в тетрадях.
Сформулируем правило умножения обыкновенной дроби на натуральное число. Проверим, правы ли вы.
Откройте учебник на странице 69. Прочитайте правило.
Сделайте запись в тетрадях правила умножения обыкновенной дроби на натуральное число в общем виде.
V Первичное закрепление изученного материала
Выполните задание на доске и в тетрадях.
1) 3/4 * 3; 4/5 * 6; 5/8 *5;
2) 5 * 3/7; 1 * 5/9; 0 * 3/17;
3) 7/12 * 36; 12 * 5/6; 12 * 1/12.
Замечание: А разве нельзя сначала сократить, а потом записывать ответ?
VI Физкультминутка
Наши ручки отложили
Руки кверху все поднимаем,
А потом их отпускаем.
А потом их развернем
И к себе скорей прижмем.
А потом быстрей, быстрей
Хлопай, хлопай веселей.
Нам сегодня не до скуки.
И за парты все вернулись –
Вновь урок у нас идёт.
VII Повторение изученного ранее материала. Работа над задачей.
Сформулируйте правило умножения обыкновенной дроби на натуральное число.
Решить задачу № 430 на доске и в тетрадях:
Вопросы:
Прочитайте задачу.
О чем говориться в задаче?
Что такое периметр?
Чему равен периметр треугольника?
Что необходимо знать, чтобы найти периметр треугольника?
Что известно про сторону АВ, ВС, АС?
Один учащийся читает вслух задачу № 430: Найдите периметр треугольника АВС, если АВ = 2/15 м, ВС больше АВ в 4 раза, а АС меньше ВС на 1/15 м?.
Учащиеся отвечают на вопросы по задаче. Один учащийся решает задачу на доске, а остальные учащиеся в тетрадях.
VIII Выполнение самостоятельной работы. Математический диктант.
Поверим, как вы усвоили тему.
Математический диктант с последующей проверкой (см. слайд).
Поменяйтесь тетрадями с соседом и проверьте его работу, выставите отметки.
Оценивание:
все задания выполнены верно - ,
допущена одна ошибка -
допущены две ошибки - ,
допущены более трех ошибок - .
Подведем итоги.
Поднимите руки, у кого ? ? ? ? Молодцы!
IX Подведение итогов урока. Рефлексия.
Подведем итого урока.
Вы сегодня – молодцы: сами поставили задачу. Какую? (отвечают), сами сформулировали тему урока. Какую? (отвечают). Используя имеющиеся знания, сами нашли правило умножение дробей.
Заполнить пропуски в тексте:
Чтобы умножить дробь на натуральное число, надо... дроби ... на это число, а знаменатель ... прежним.
Оценки
X Домашнее задание – 2 мин.
Учитель дает рекомендации по выполнению домашнего задания:
1. Прочитать пункт 13 до задачи 2.
2. Выучить правило умножения обыкновенной дроби на натуральное число на стр. 69
3. Творческое задание: Написать рассказ, историю, сказку по теме урока
Закончить наш урок хотелось бы цитатами
. Л.Н. Толстой
Я получила удовольствие от работы с вами, а вы надеюсь от решения новых задач, до свидания, спасибо за урок!.
Используемая литература.
Учебник для 6 класса , авторы Н.Я. Виленкин, В.И.Жохов, А.С., Чесноков, С.И. Шварцбурд.
http://festival.1september.ru/articles/418012/
Материал урока М. Н. Литвиной
http://school-collection.edu.ru/catalog/res/16c9e4ed-25c5-4df2-9e05-a1c5d7643472/?from=
608887c4-68f4-410f-bbd4-618ad7929e22&interface=pupil&class[]=47&class[]=48&subject=16
http://school-collection.edu.ru/catalog/res/5509e3c1-2f2c-4070-8d4f-5c59413c769c/?from=
608887c4-68f4-410f-bbd4-618ad7929e22&interface=pupil&class[]=47&class[]=48&subject=16