Технологическая карта урока
Предмет: Геометрия
Класс: 8 класс
Учебник: Геометрия 7-9 классы: учеб. для общеобразоват. учреждений/ [Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.] – 20-е изд. – М.: Просвещение, 2010. – 384 с. Глава VI, параграф 1
Тема урока: Площадь многоугольника
Тип урока: Урок изучения нового
Учебная задача урока: в совместной деятельности с учащимися ввести понятие площади многоугольника, свойства площадей, единицы измерения площади, формулу площади прямоугольника и доказать её.
Диагностируемые цели урока:
В результате урока ученик
Знает
- понятие площади фигуры;
- свойства площадей;
- единицы измерения площади, их различные виды и связь между ними;
- теорему о площади прямоугольника и её доказательство.
Умеет
- измерять площади фигур с помощью палетки
- применять формулы нахождения площади квадрата и прямоугольника для
решения задач;
- переводить из одной единицы измерения площади в другую;
-доказывать теорему о площади прямоугольника.
Понимает
- как находить площадь фигуры с помощью палетки;
- что свойства площадей принимаются без доказательства
-что доказательство теоремы о площади прямоугольника основано на свойствах площадей.
Планируемые результаты (УУД):
Личностные: умение учащегося устанавливать связи между целью учебной деятельности и ее мотивом, т.е. между результатом учения, и тем, что побуждает к деятельности, ради чего она осуществляется, таким образом, должна осуществляться осмысленная организация собственной деятельности ученика.
Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно, планирование – определение последовательности промежуточных целей с учетом конечного результата, оценка- выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т.е. определение цели сотрудничества, функций участников, способов взаимодействия, умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и дидактической формами речи в соответствии с грамматическими и синтактическими нормами родного языка, умение доказывать собственное мнение.
Познавательные: анализ объектов с целью выделения признаков (существенных, несущественных); выдвижение гипотез и их обоснование; построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей.
Предваряющее домашнее задание:
Сделать модели прямоугольника, квадрата, двух равных фигур и четырехугольника общего вида.
На прозрачной пленке нанести параллельные вертикальные и горизонтальные прямые, расстояние между которыми 1 см, т.е. разбить пленку на квадраты со стороной 1 см.
Организационная структура урока
| Этап урока | Деятельность учителя | Деятельность учащихся |
|
|
| Познавательная | Коммуникативная | Регулятивная |
|
| Осуществляемые действия | Осуществляемые действия | Формируемые способы деятельности | Осуществляемые действия | Формируемые способы деятельности | Осуществляемые действия | Формируемые способы деятельности |
| Организационный момент. | Приветствует учащихся. Отмечает отсутствующих. Проверяет готовность учащихся к уроку. Сообщает тему и структуру урока | Отвечают на вопросы учителя по поводу отсутствия учащихся. Настраиваются на работу. | Постановка цель деятельности как ответ на вопрос: «Что я хочу узнать сегодня на уроке?». | Взаимодействуют с учителем во фронтальном режиме. Концентрируют внимание.
| Слушать и слышать собеседника. Планирование учебного сотрудничества с учителем и одноклассниками. | Получают позитивный заряд. | Самоопределение и настраивание на урок. |
| Актуализация знаний. | Организует повторение понятия длины отрезка, единиц измерения длин отрезков, свойств измерения длин отрезков, понятий квадрата и прямоугольника. Организует устное, фронтальное решение заданий типа: см. приложение 1. | Повторяют понятие длины отрезка, единицы измерения длин отрезков, свойства измерения длин отрезков, понятия квадрата и прямоугольника. | Анализирование и сравнение предлагаемых заданий с целью извлечения необходимой информации для построения математического высказывания. | Взаимодействуют с учителем во фронтальном режиме. Выполняют задания.
| Слушать и слышать собеседника. Выражение своих мыслей с достаточной полнотой и точностью, использование дополнительных высказываний для обоснования своего суждения. | Закрепляют умения находить длину отрезка, определять форму фигуры. Самоконтролируют процесс выполнения заданий
| Адекватное самостоятельное оценивание правильности выполнения заданий и внесение необходимых корректив в решения
|
| Мотивация. Создание проблемной ситуации. | См. приложение 2. | Построение логической цепи рассуждений, выдвижение гипотез и их обоснование. | Анализирование и сравнение предлагаемых заданий с целью извлечения необходимой информации для построения математического высказывания. | Взаимодействуют с учителем во фронтальном режиме. Отвечают на задаваемые вопросы в процессе обсуждения, сотрудничают в поиске и выборе информации. | Слушать и слышать собеседника. Выражение своих мыслей с достаточной полнотой и точностью, использование дополнительных высказываний для обоснования своего суждения. | Участвуют в диалоге и выводят, что нужно изучить понятие площади многоугольника. | При возникновении ситуации затруднения регулировка хода мысли. |
| Формирование проблемы: тема и цель урока | Выводит на формулировку темы и цели урока. Четко проговаривает тему и цель урока. | Изучить понятие площади многоугольника. | Анализирование и сравнение предлагаемых заданий с целью извлечения необходимой информации для построения математического высказывания. Анализ объектов с выделением существенных и несущественных признаков. Составление плана достижения цели и определения средств её достижения. | Взаимодействуют с учителем во фронтальном режиме. Выходят на необходимость изучения понятия площади многоугольника. | Слушать и слышать собеседника. Выражение своих мыслей с достаточной полнотой и точностью, использование дополнительных высказываний для обоснования своего суждения. | Участвуют в диалоге. | При возникновении ситуации затруднения регулировка хода мысли. Самоопределение. |
| «Открытие» нового знания | Организует работу по открытию понятия площади многоугольника и свойств площадей, единицы измерения площади, теоремы о площади прямоугольника и её доказательства: См. приложение 3. | Учатся применять понятие площади многоугольника в процессе «открытия» нового знания | Выделение необходимой информации, планирование , своей деятельности, прогнозирование результата | Взаимодействуют с учителем во фронтальном режиме. Работа в парах: измеряют площади фигур с помощью палетки. Отвечают на задаваемые вопросы в процессе обсуждения, сотрудничают в поиске и выборе информации. | Слушать и слышать собеседника. Выражение своих мыслей с достаточной полнотой и точностью, использование дополнительных высказываний для обоснования своего суждения. | Участвуют в диалоге. При необходимости исправляют ошибки, добавляют аргументацию.
| Проявление познавательной инициативы. При возникновении ситуации затруднения регулировка хода мысли. |
| Первичное применение нового знания | Организует работу по выполнению упражнений на нахождение площадей квадрата и прямоугольника: см. приложение 4. | Учатся применять формулы площади квадрата и прямоугольника в процессе самостоятельного решения или работы у доски.
| Самостоятельное планирование своей деятельности, применение формул площади квадрата и прямоугольника в процессе самостоятельного решения и прогнозирование результата. Выстраивание в процессе решения задач логической цепи рассуждений. | Взаимодействуют с учителем во фронтальном режиме.
| Слушать и слышать собеседника. Выражение своих мыслей с достаточной полнотой и точностью, использование дополнительных высказываний для обоснования своего суждения. Планирование сотрудничества с одноклассниками и учителем, координирование своих действий. | Закрепляют умения применять формулы площади квадрата и прямоугольника для решения задач. Самоконтролируют процесс выполнения заданий.
| Проявление познавательной инициативы. Адекватное самостоятельное оценивание правильности выполнения заданий и внесение необходимых корректив в решения. |
| Рефлексия | Организует обсуждение как ответы на вопросы: «Какова была цель урока? Достигли мы её? Как мы её достигли?». | Отвечают на вопросы: «Какова была цель урока? Достигли мы её? Как мы её достигли?». | Рефлексия способов и условий своих действий. | Взаимодействуют с учителем во фронтальном режиме.
| Слушать и слышать собеседника. Использование различных критериев для обоснования своих суждений. | Участвуют в диалоге. При необходимости исправляют ошибки, добавляют аргументацию.
| Проведение самооценки. |
| Домашнее задание | Глава VI, параграф 1, № 449 (а, б), 450 (а, б), 452 (б), 454 (б) См. приложение 5. |
Приложение 1.
Актуализация знаний
(фронтальная работа со всем классом)
- Выберете из предложенных фигур многоугольники:






 1. 2. 3. 4. 5. 6. 7.
1. 2. 3. 4. 5. 6. 7.
Многоугольники изображены под номерами 1, 2, 3, 5, 7.
-Какие из них являются прямоугольниками?
Ответ: 5 и 7
-Какие из них являются квадратами?
Ответ: 7
- Как связаны понятия прямоугольника и квадрата?
Квадрат – это прямоугольник, у которого две смежные стороны равны.
- Укажите длины отрезков, представленных на рисунке, если за единицу измерения выбрана 1 клетка, равная 1 см.
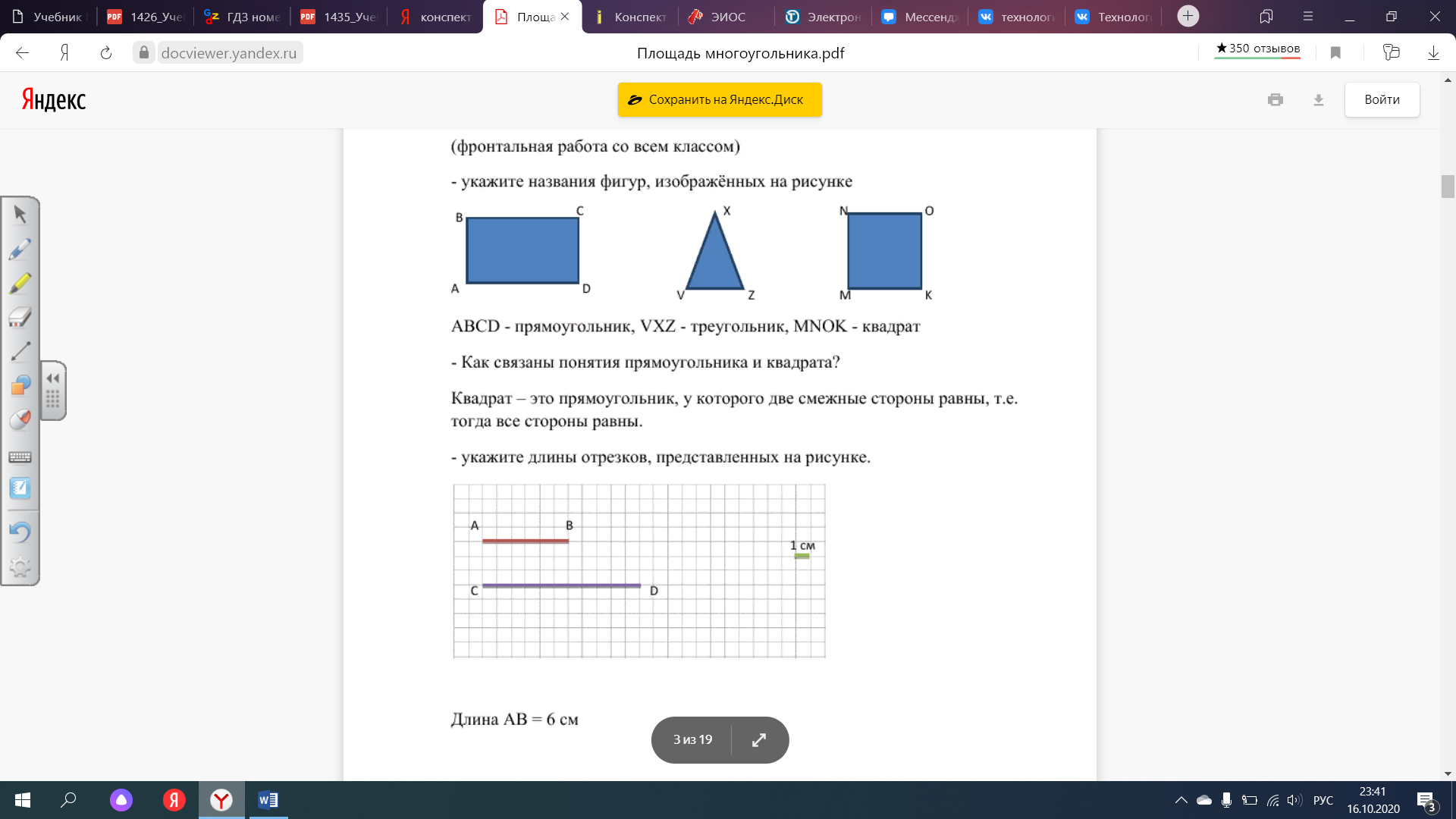
Длина AB = 6 см
Длина CD = 11 см
- Каким числом выражается длина отрезка
Положительным числом
- Что показывает это число?
Сколько раз единичный отрезок или его части убираются в измеряемом отрезке.
- Какие существуют единицы измерения длин отрезков и как они связаны?
Единицы измерения длин отрезков: мм, см, дм, м, км.
1 см = 10 мм;
1 дм = 10 см = 100 мм;
1 м = 10 дм = 100 см = 1 000 мм;
1 км = 1 000 м.
Задача 1 По данным рисунка найдите длину отрезка МК (ответ дайте в мм)
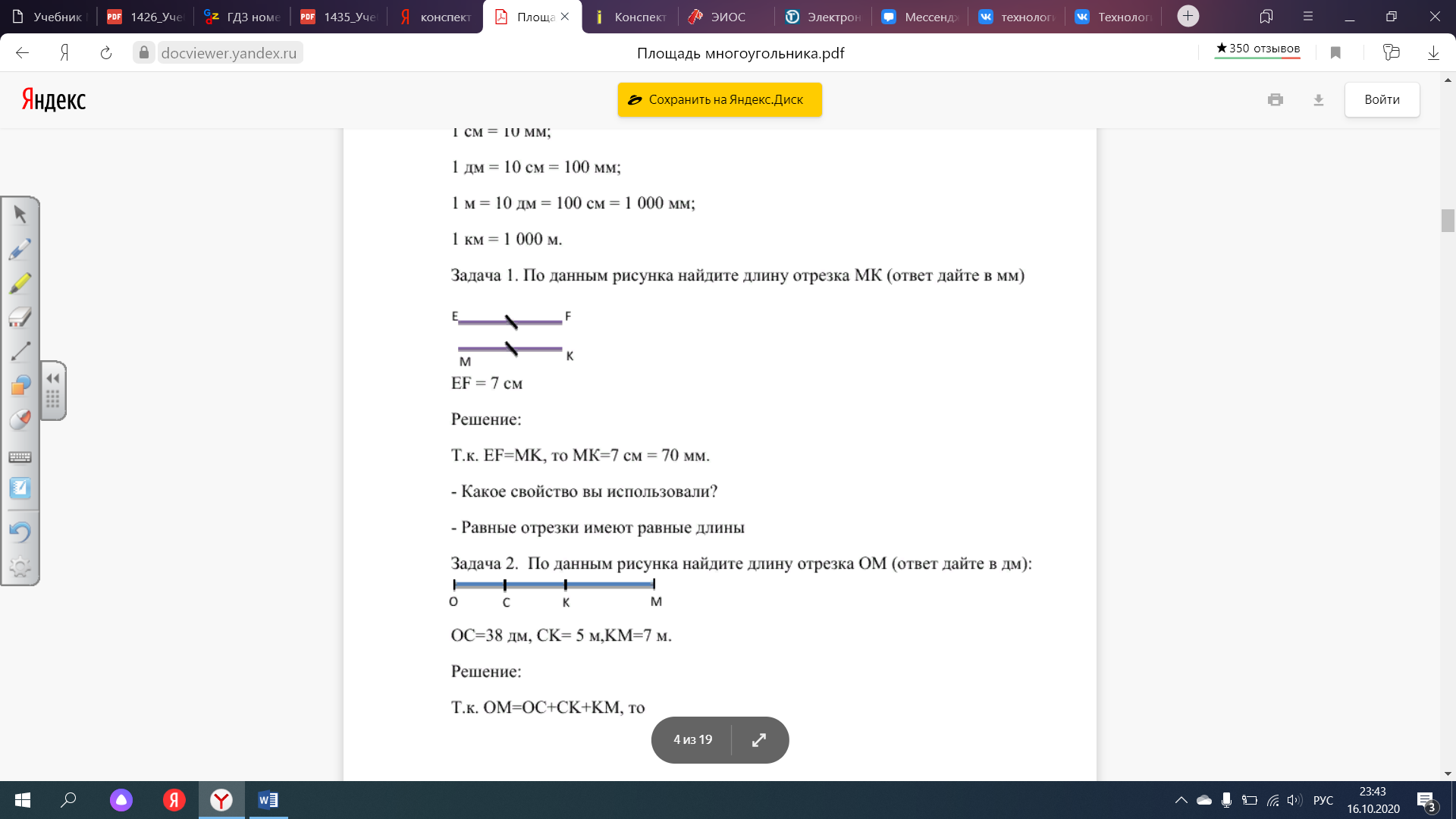
EF = 7 см
Решение:
Т.к. EF=MK, то МК=7 см = 70 мм.
- Какое свойство вы использовали?
Равные отрезки имеют равные длины
Задача 2 По данным рисунка найдите длину отрезка ОМ (ответ дайте в дм)

OC=38 дм, CK= 5 м,KM=7 м.
Решение:
Т.к. OM=OC+CK+KM, то
OM= 38 дм + 5 м + 7 м = 38дм +50дм+70дм=158 дм
- Какое свойство вы использовали?
Если отрезок составлен из нескольких других отрезков, то его длина равна сумме длин этих отрезков.
Приложение 2
Мотивация
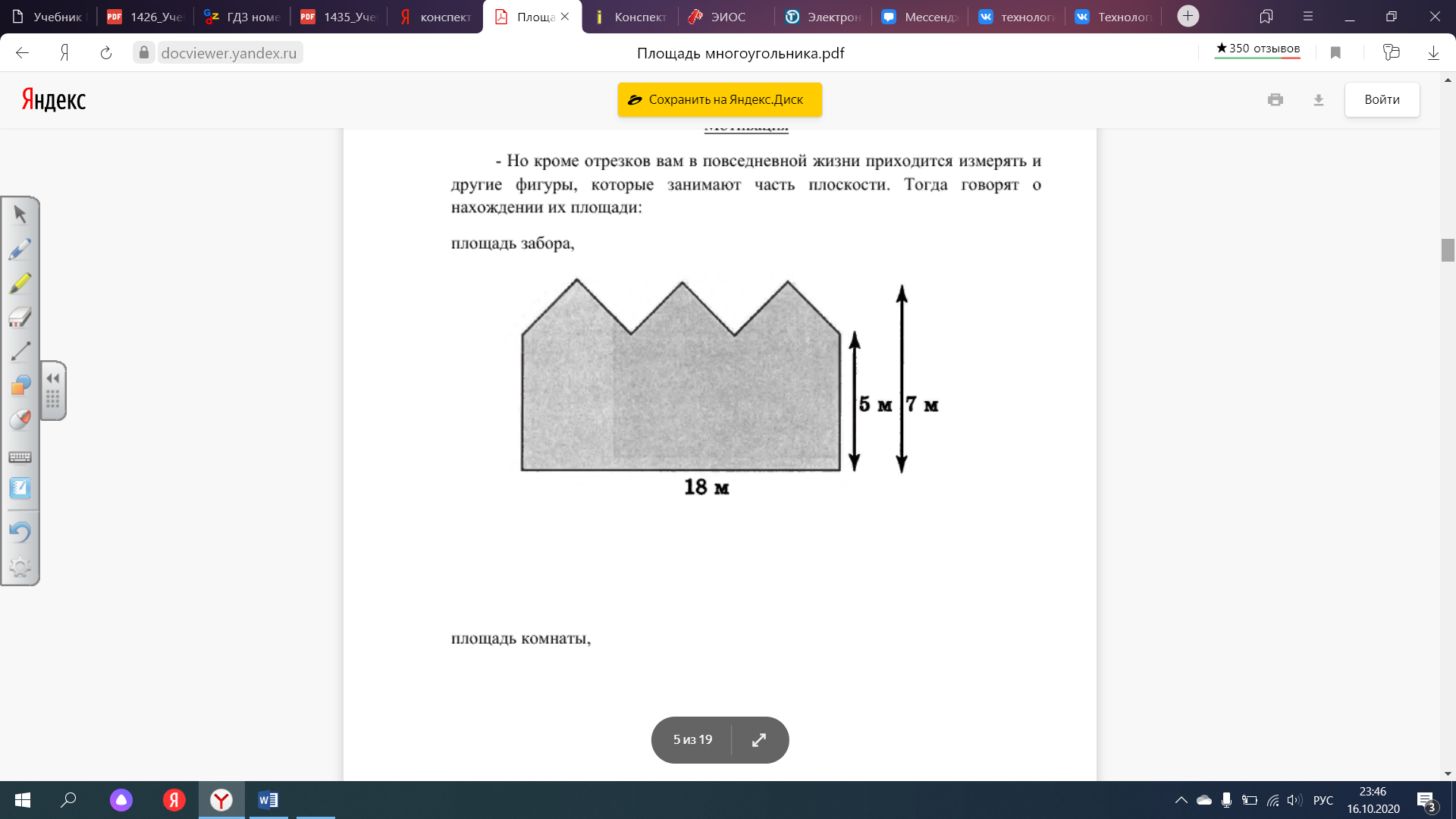
- Но кроме отрезков в повседневной жизни приходится измерять и другие фигуры, которые занимают часть плоскости. Тогда говорят о нахождении их площади:
площадь забора,
площадь комнаты,
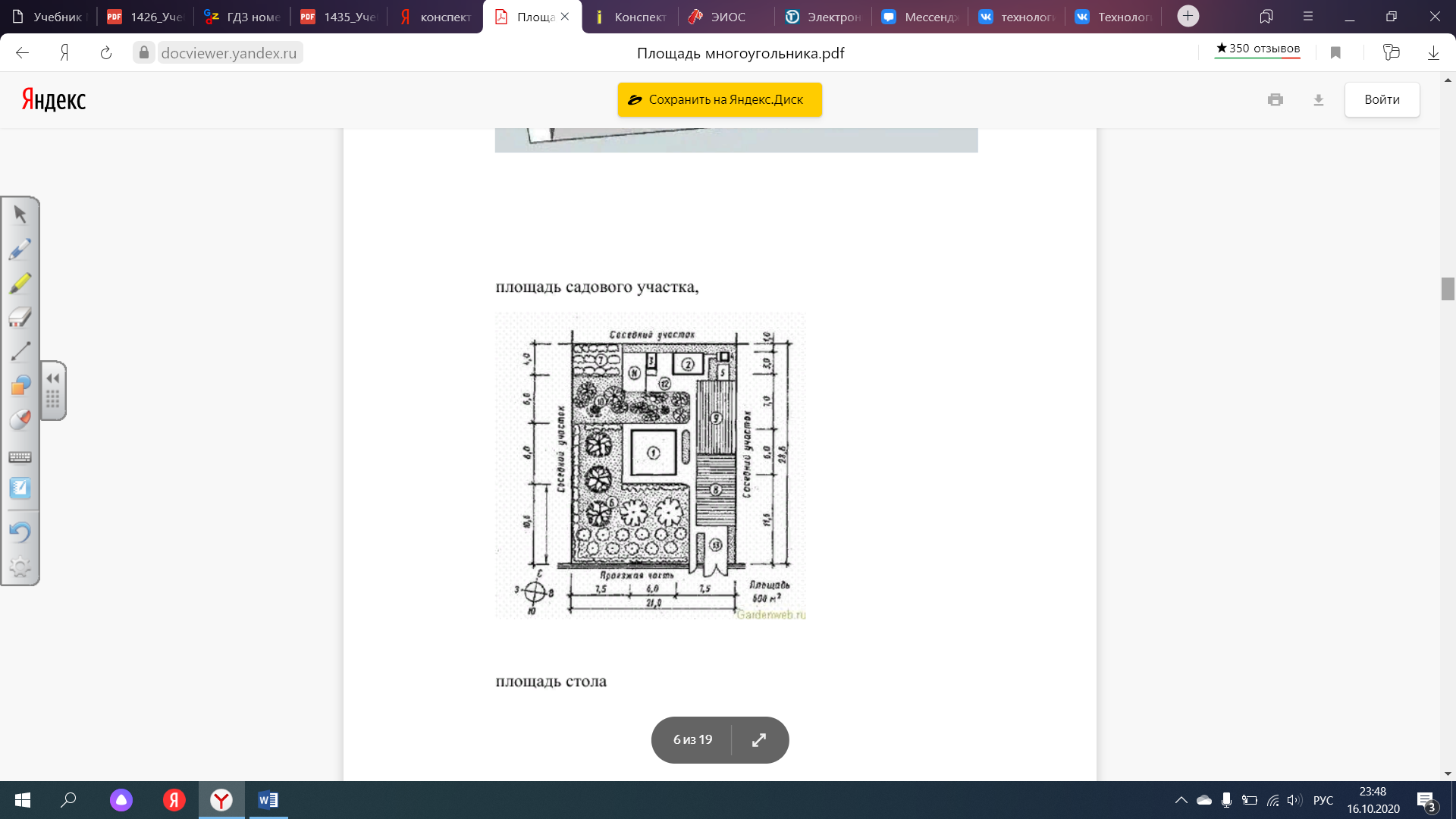
площадь садового участка
Приложение 3 Открытие нового знания.
Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник. Измерение площадей проводится с помощью выбранной единицы измерения аналогично измерению длин отрезков. За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков. Так, если за единицу измерения отрезков принят сантиметр, то за единицу измерения площади принимают квадрат со стороной 1 см.
Такой квадрат называется квадратным сантиметром и обозначается см2. Аналогично определяется квадратный метр (м2), квадратный миллиметр (мм2) и т.д.
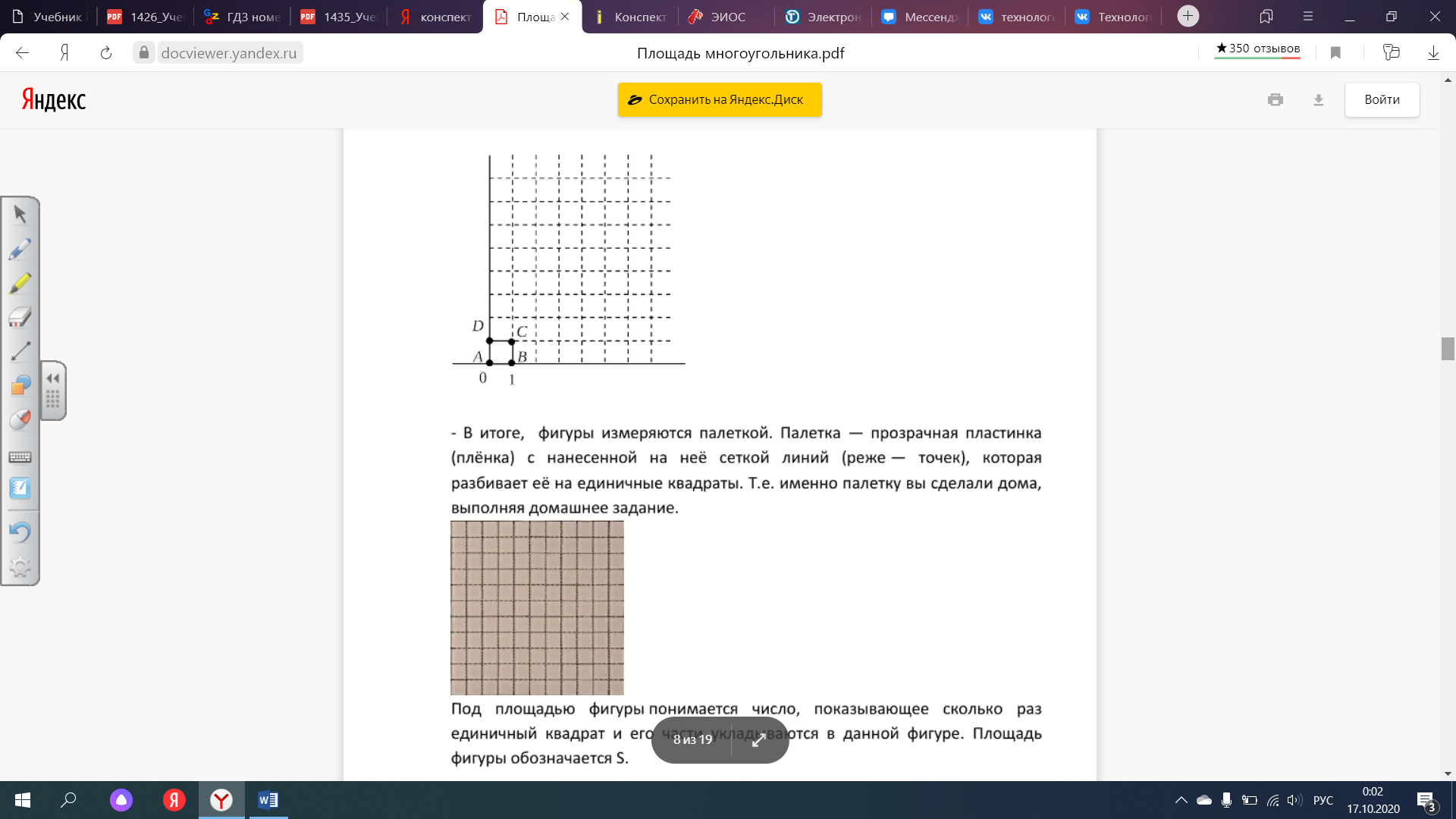
- Плоские фигуры измеряются палеткой. Палетка — прозрачная пластинка (плёнка) с нанесенной на неё сеткой линий (реже — точек), которая разбивает её на единичные квадраты. Т.е. именно палетку вы сделали дома, выполняя домашнее задание.


Под площадью фигуры понимается число, показывающее сколько раз единичный квадрат и его части укладываются в данной фигуре. Площадь фигуры обозначается S.
Например, измерим площадь данной плоской фигуры.
Наложим на неё палетку:
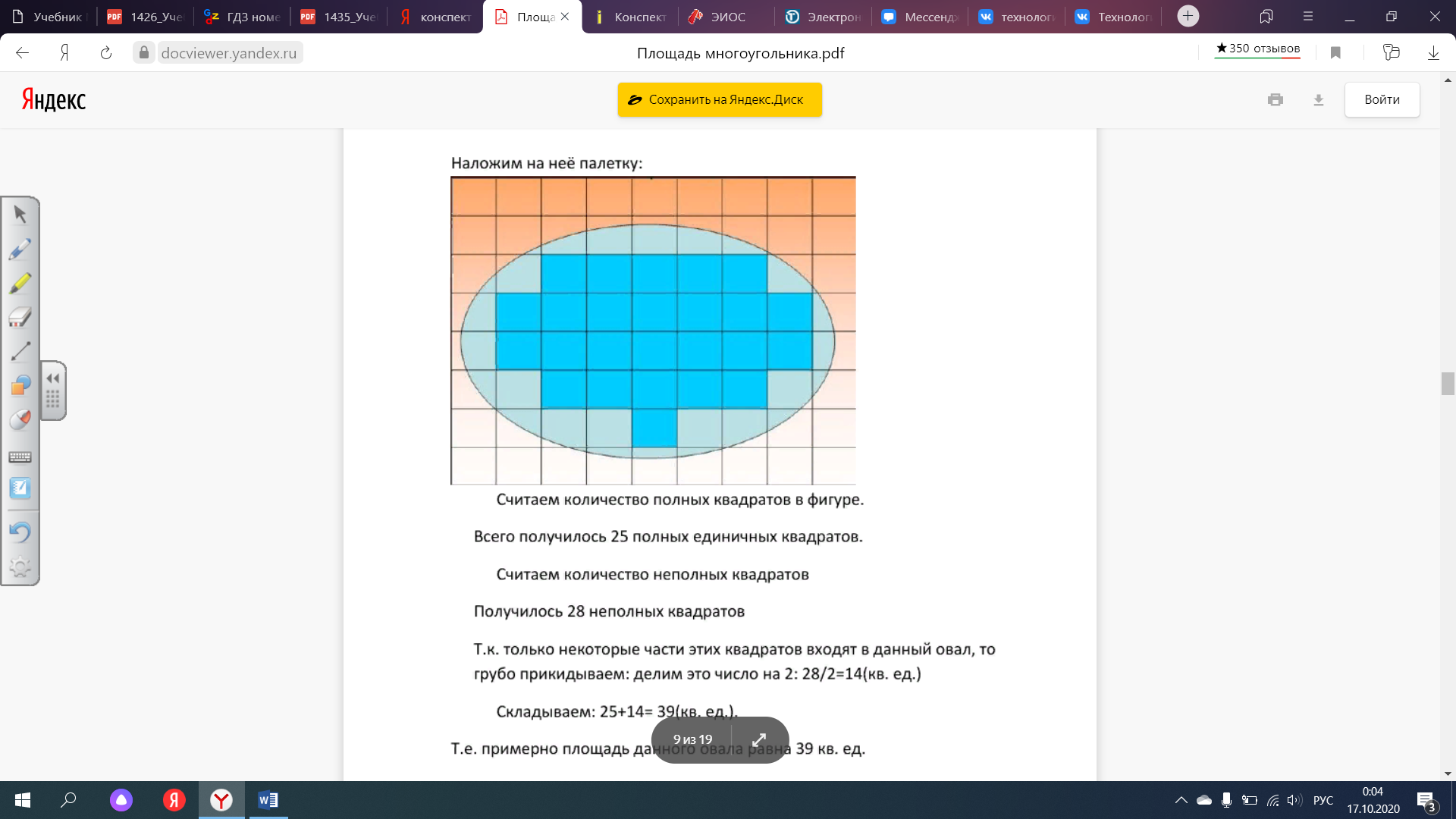
Считаем количество полных квадратов в фигуре.
Всего получилось 25 полных единичных квадратов.
Считаем количество неполных квадратов
Получилось 28 неполных квадратов
Т.к. только некоторые части этих квадратов входят в данную фигуру, то грубо прикидываем, деля это число на 2: 28/2=14(кв. ед.)
Складываем: 25+14= 39(кв. ед.).
Т.е. примерно площадь данной фигуры равна 39 кв. ед.
- Итак, каким по знаку должно быть число, определяющее площадь фигуры?
Ответ: положительным.
Единицы измерения площадей как единицы измерения длин отрезков бывают разные: км2, м2, дм2, см2, мм2 и др.
Т.к. 1 км = 1000 м, то 1 км2=10002 м2=1 000 000 м2
Т.к. 1 м = 10 дм, то 1 м2= 102 дм2=100 дм2,
Т.к. 1 дм = 10 см, то 1 дм2= 102 см2=100 см2,
Т.к. 1 см = 10 мм, то 1 см2= 102 мм2=100 мм2,
На практике также используются такие единицы измерения площади:
1 ар=1 сотка = 100 м2
1 гектар = 1 га = 10 000 м2 = 100 соток
Работа в парах:
Измерьте палеткой площади фигур соседа по парте:
1.
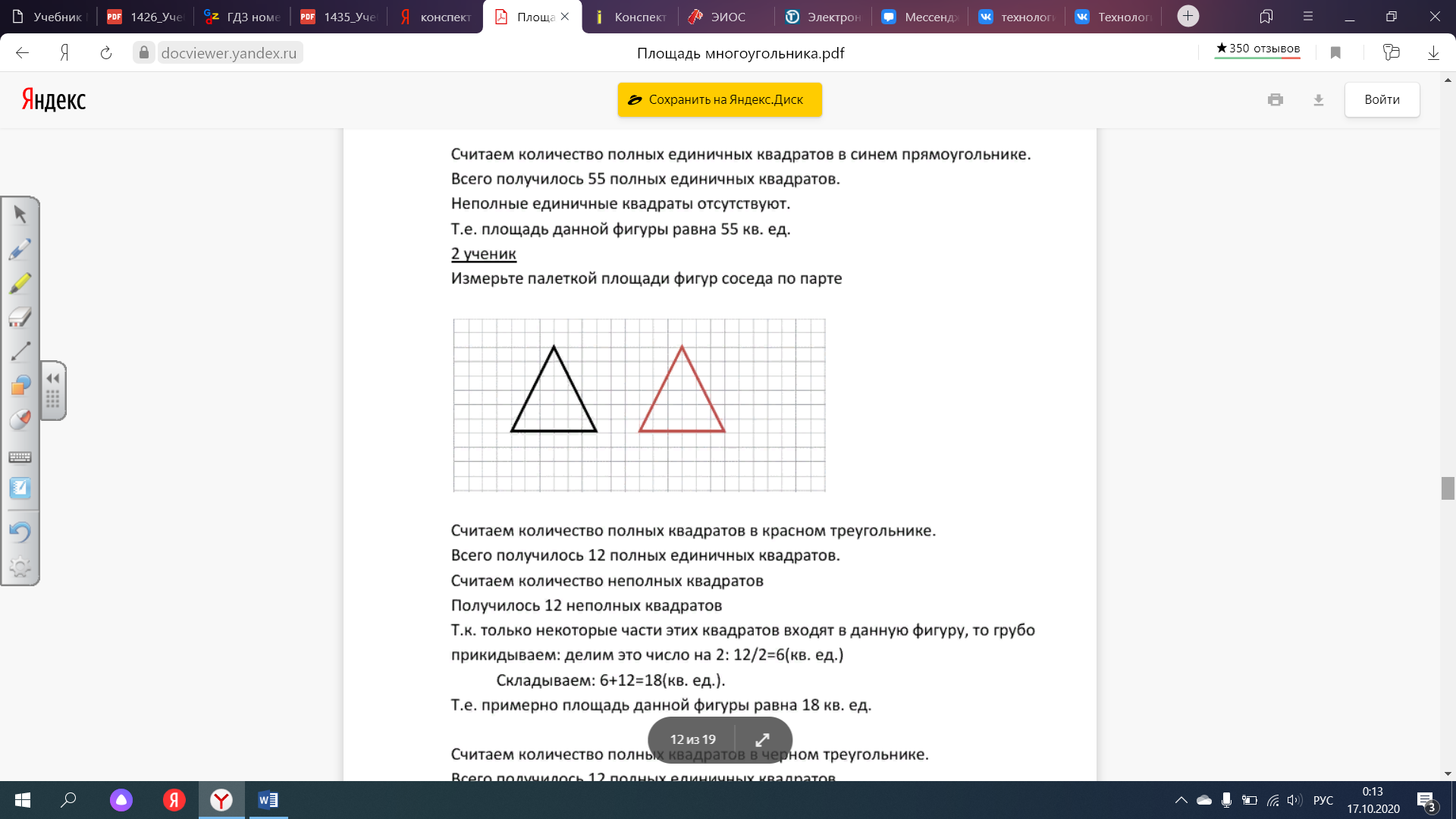
Считаем количество полных квадратов в красном треугольнике.
Всего получилось 12 полных единичных квадратов.
Считаем количество неполных квадратов
Получилось 12 неполных квадратов
Т.к. только некоторые части этих квадратов входят в данную фигуру, то грубо прикидываем: делим это число на 2: 12/2=6(кв. ед.)
Складываем: 6+12=18(кв. ед.).
Т.е. примерно площадь данной фигуры равна 18 кв. ед.
Считаем количество полных квадратов в черном треугольнике.
Всего получилось 12 полных единичных квадратов.
Считаем количество неполных квадратов
Получилось 12 неполных квадратов
Т.к. только некоторые части этих квадратов входят в данную фигуру, то грубо прикидываем: делим это число на 2: 12/2=6(кв. ед.)
Складываем: 6+12=18(кв. ед.).
Т.е. примерно площадь данной фигуры равна 18 кв. ед.
2.
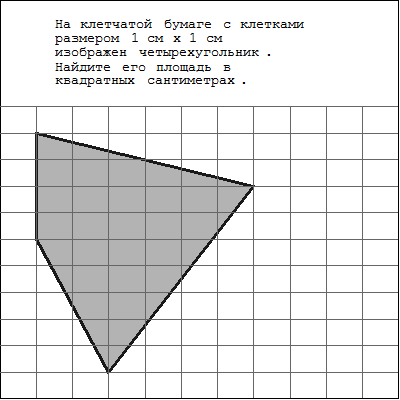
Считаем количество полных квадратов в этой фигуре. Всего получилось 18 полных единичных квадратов.
Считаем количество неполных квадратов. Всего получилось 20 неполных квадратов. Делим полученное число на 2: 20:2=10.
Т.е. примерно площадь данной фигуры равна18+10=28 кв. ед.
3. 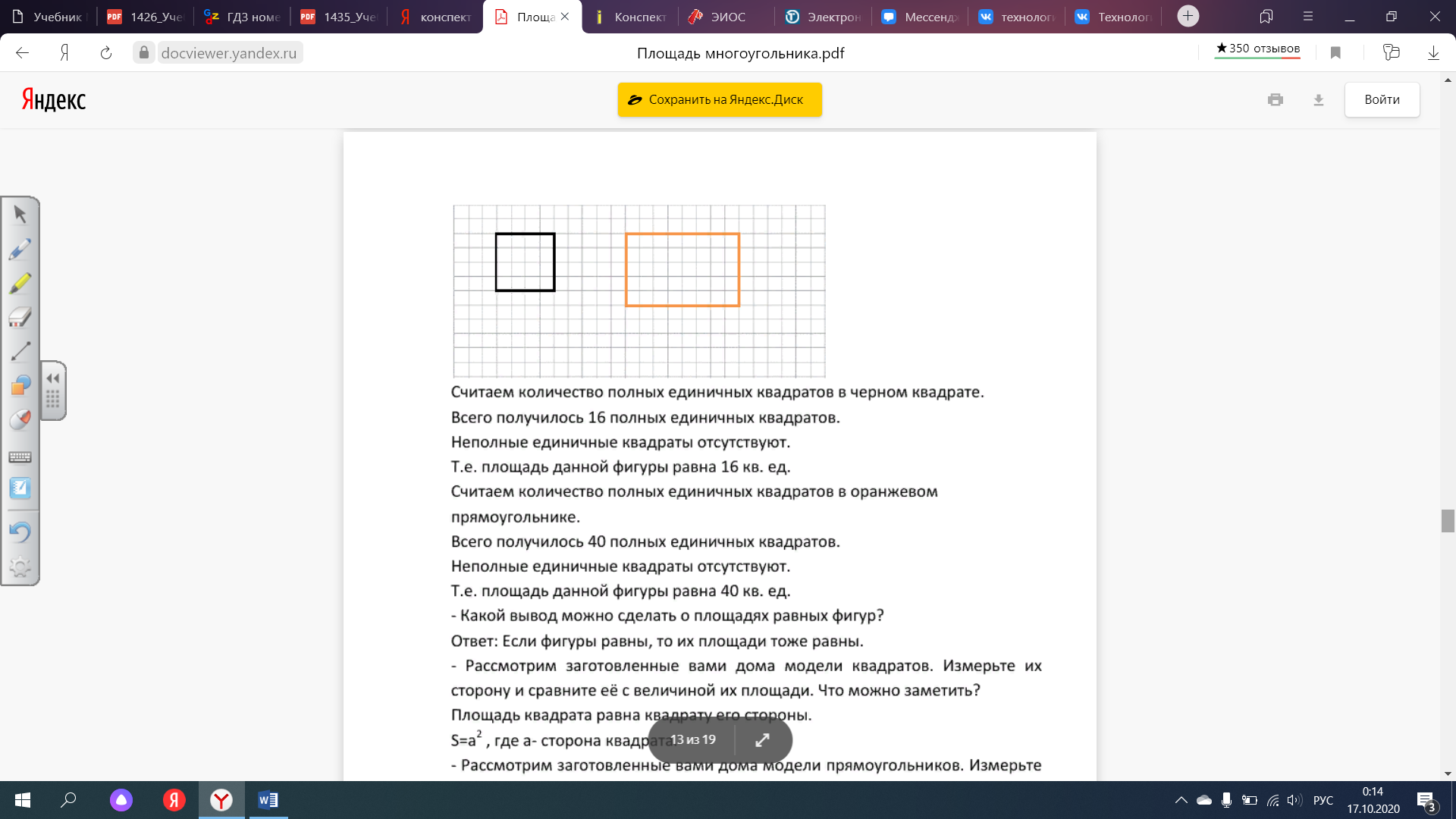
Считаем количество полных единичных квадратов в квадрате.
Всего получилось 16 полных единичных квадратов.
Неполные единичные квадраты отсутствуют.
Т.е. площадь данной фигуры равна 16 кв. ед.
Считаем количество полных единичных квадратов в прямоугольнике.
Всего получилось 40 полных единичных квадратов.
Неполные единичные квадраты отсутствуют.
Т.е. площадь данной фигуры равна 40 кв. ед.
-Сравните 2 треугольника?
Эти треугольники равны
- Какой вывод можно сделать о площадях равных фигур?
1. Равные многоугольники имеют равные площади.
-Возьмем 3 фигуру и разделим ее на две части.


2
1

Найдем площадь каждой.
Считаем количество полных и неполных квадратов в первой части. Полные единичные квадраты отсутствуют, 10 неполных ед.кв. Делим это число на 2: 10:2=5 ед.кв.
Площадь первой части примерно равна: 0+5=5 ед.кв.
Считаем количество полных и неполных квадратов во второй части. Получили 13 полных ед.кв., 20 неполных ед.кв. Делим это число на 2: 20:2=10 ед.кв.
Площадь второй части примерно равна: 13+10=23 ед.кв.
Сравним площадь вей фигуры с суммой площадей первой и второй частей.
Они равны.
- Какой общий вывод можно сделать?
2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
- Рассмотрим модель квадрата. Измерьте его сторону и сравните её с величиной его площади. Что можно заметить?
3. Площадь квадрата равна квадрату его стороны.
S=a2 , где а- сторона квадрата.
- Рассмотрим модель прямоугольника. Измерьте его стороны и сравните их с величиной его площади. Что можно заметить?
Площадь прямоугольника равна произведению его смежных сторон.
S=a*b, где a, b – смежные стороны прямоугольника.
Теорема. Площадь прямоугольника равна произведению его смежных сторон.
Дано: АВСD - прямоугольник
АВ=а, ВС=b
Доказать: S АВСD =a*b
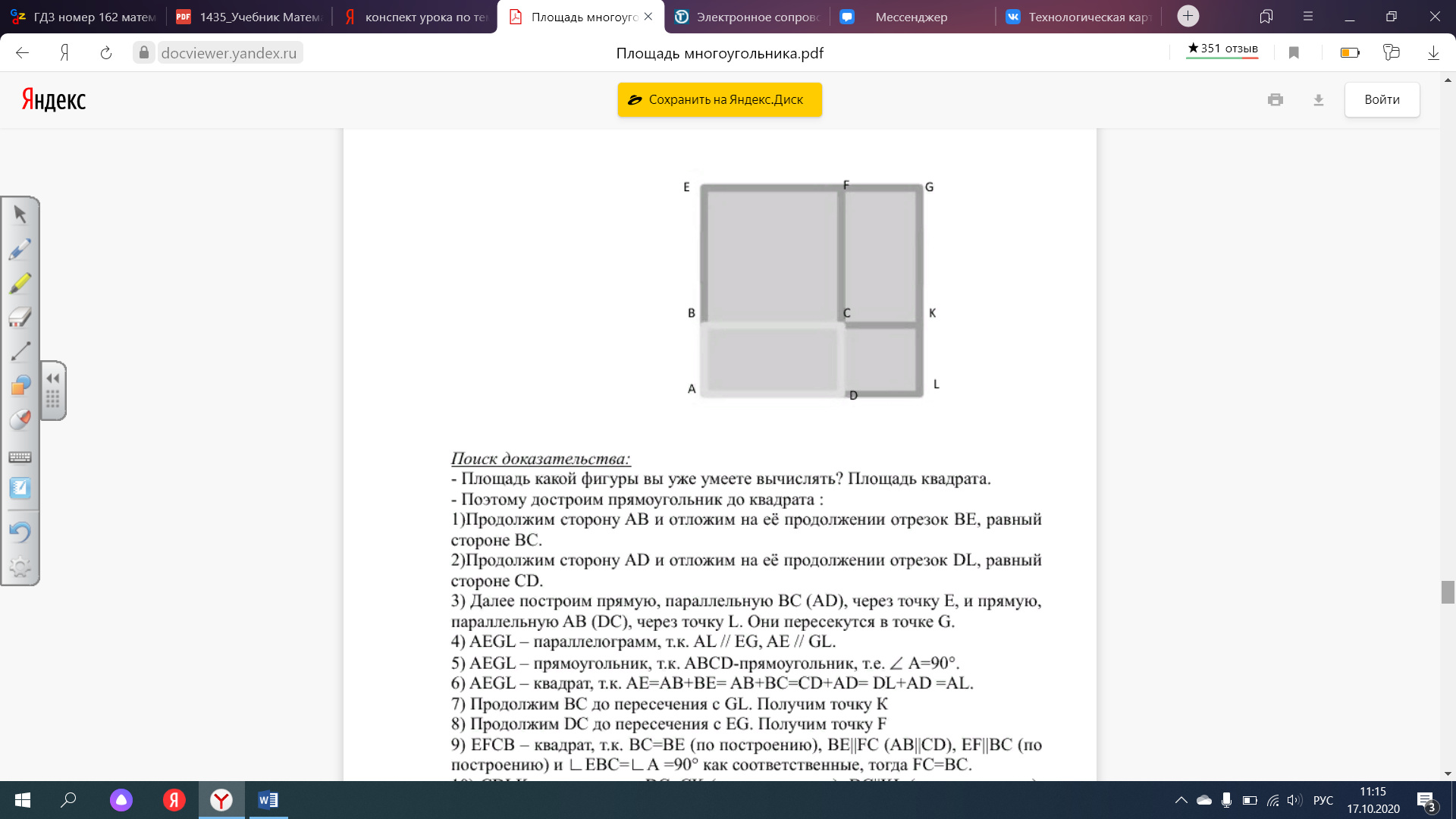
Поиск доказательства:
- Площадь какой фигуры вы уже умеете вычислять? Площадь квадрата.
- Поэтому достроим прямоугольник до квадрата:
1)Продолжим сторону AB и отложим на её продолжении отрезок BE, равный стороне BC.
2)Продолжим сторону AD и отложим на её продолжении отрезок DL, равный стороне CD.
3) Далее построим прямую, параллельную BC (АD), через точку Е, и прямую, параллельную AB (DC), через точку L. Они пересекутся в точке G.
4) AEGL – параллелограмм, т.к. AL // EG, AE // GL.
5) AEGL – прямоугольник, т.к. ABCD-прямоугольник, т.е. ∠А=90°.
6) AEGL – квадрат, т.к. AE=AB+BE= AB+BC=СD+АD= DL+АD =AL.
7) Продолжим ВС до пересечения с GL. Получим точку К
8) Продолжим DС до пересечения с EG. Получим точку F
9) EFCB – квадрат, т.к. BC=BE (по построению), BE||FC (АB||CD), EF||BC (по построению) и ∟EBC=∟А =90° как соответственные, тогда FC=BC.
10) CDLK – квадрат, т.к. DC=CK (по построению), DC||KL (по построению), CK||DL (ВC||АD) и ∟CDL=∟А =90° как соответственные, тогда CK=CD.
11) FGKC – прямоугольник, равный исходному, т.к. FG // CK (EF||BC),
FC//GK
(CD||GL),
CK=CD,
FC=BC,
∟A=∟CDL=∟FCK=90° как соответственные.
-Итак, на какие фигуры разбит полученный квадрат AEGL?
На 2 равных прямоугольника ABCD и CFGK и 2 квадрата BEFC и DCKL со сторонами а и b соответственно.
- Запишем площадь каждой фигуры на рисунке:
SALGE=(a+b)2
SABCD=SCFGK
SBEFC=a*a=a2
SCDKL=b*b=b2
По № 2 свойству площадей площадь большого квадрата равна сумме площадей фигур, содержащихся в нем. Получили:
(a+b)2 =2SABCD +a2 +b2
Распишем квадрат суммы двух чисел в левой части:
a2 +2*a*b+b2 =a2 +2*SABCD+b2
- Что можно вычесть из обеих частей равенства?
Ответ: вычтем a2 +b2
- Что тогда получается?
Ответ: получим 2*a*b=2*S ABCD
- Выразите площадь АВСD
SABCD =a*b.
Доказательство:
1) Дополнительные построения:
а) BE = BC, Е AB
б) DL = CD, L 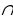 AD
AD
в) Е G // BC (АD), LG// AB (DC).
г) ВС 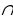 GL = К
GL = К
д) DС 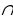 EG = F
EG = F
2) AEGL – параллелограмм (по определению параллелограмма ), т.к. AL // EG, AE // GL.
3) AEGL – прямоугольник (по определению прямоугольника), т.к. ABCD-прямоугольник, т.е. ∠А=90°.
4) AEGL – квадрат (по определению квадрата), т.к. AE=AB+BE= AB+BC=СD+АD= DL+АD =AL.
5) EFCB – квадрат (по определению квадрата), т.к. BC=BE (по построению), BE||FC (АB||CD), EF||BC (по построению) и ∟EBC=∟А =90° как соответственные, тогда FC=BC.
6) CDLK – квадрат (по определению квадрата), т.к. DC=CK (по построению), DC||KL (по построению), CK||DL (ВC||АD) и ∟CDL=∟А =90° как соответственные, тогда CK=CD.
7) FGKC – прямоугольник (по определению прямоугольника), равный исходному, т.к. FG // CK (EF||BC), FC//GK (CD||GL), CK=CD, FC=BC, ∟A=∟CDL=∟FCK=90° как соответственные.
8)
S AEGL= (а+b)2 (по свойству площадей № 3)
S ABCD=S CFGK (по свойству площадей № 1)
S BEFC=a*a=a2 (по свойству площадей № 3)
S CDKL=b*b=b2 (по свойству площадей № 3)
9) по свойству площадей № 2 S AEGL= S ABCD+S CFGK+ S BEFC+ S CDKL.
(a+b)2 =2SABCD +a 2+b2
a 2+2*a*b+b2 =a2 +2SABCD +b2 /- (a2 +b2 )
2*a*b=2*S ABCD
SABCD =a*b.
Приложение 4 Применение нового знания
№449 (в). Найдите площадь квадрата, если его сторона равна: в) 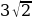 м.
м.
Решение: Sкв=а2, где а – сторона квадрата.
в) Sкв=( 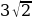 м)2 =
м)2 = 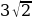 м *
м * 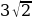 м = 18 м2.
м = 18 м2.
№450 (в). Найдите сторону квадрата, если его площадь равна: в) 12 м2.
Решение: Sкв=а2, где а – сторона квадрата, значит а=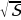
в) а = 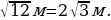
№452 (а). Пусть a и b- смежные стороны прямоугольника, а S - его площадь.
Вычислите: а) S, если а=8,5 см, b=3,2 см
Решение:
S=a*b= 8,5 * 3,2= 27,2 см2
Ответ: 27,2 см2
№454(а). Найдите стороны прямоугольника, если: а) его площадь равна 250 см2 , а одна сторона в 2,5 раза больше другой
Решение:
а=2,5*b
S=a*b=2,5*b2
250=2,5*b2
b=10 см
a=b*2,5= 25см
Ответ: а = 25 см, b = 10 см
Приложение 5 Домашнее задание
№449 (а, б). Найдите площадь квадрата, если его сторона равна: а) 1,2 см; б) 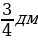 .
.
Решение: Sкв=а2, где а – сторона квадрата.
а) Sкв= (1,2 см)2=1,2 см * 1,2 см = 1,44 см2.
б) Sкв= =
= 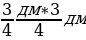 =
= 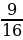 дм2.
дм2.
№450 (а, б). Найдите сторону квадрата, если его площадь равна: а) 16 см2; б) 2,25 дм2.
Решение: Sкв=а2, где а – сторона квадрата, значит а=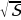
а) а = 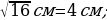
б) а = 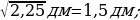
№452 (б). Пусть a и b- смежные стороны прямоугольника, а S - его площадь.
Вычислите: б) S, если а=2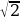 см, b=3 см
см, b=3 см
Решение:
S=a*b=2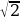 *3=6
*3=6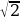
Ответ: 6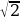 см2
см2
№454(б). Найдите стороны прямоугольника, если: б) если его площадь равна 9 м2 , а периметр равен 12 м
Решение:
S=a*b= 9
Р=2*(a+b) =12
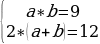
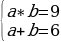 a=b=3 м
a=b=3 м
Ответ: a=3м, b=3 м













 1. 2. 3. 4. 5. 6. 7.
1. 2. 3. 4. 5. 6. 7. 












 AD
AD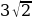 м.
м.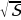
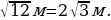
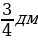 .
. =
= 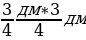 =
= 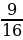 дм2.
дм2.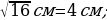
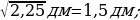
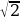 см, b=3 см
см, b=3 см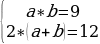
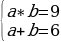 a=b=3 м
a=b=3 м









