Площади многоугольников

Площади многоугольников

Цели работы:

• Углубить и систематизировать свои знания по геометрии

• Попытаться применить знания, полученные в результате изучения данной темы при решении практических задач

Введение:

Первые геометрические понятия возникли в доисторические времена. Практическая деятельность человека служила основой длительного процесса выработки отвлеченных понятий, открытия простейших геометрических зависимостей и соотношений. Начало геометрии было положено в древности при решении чисто практических задач. Со временем, когда накопилось большое количество геометрических фактов, у людей появилось потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Постепенно создавалась геометрическая наука.

Историческая справка

Многие факты геометрии были известны древним грекам две с лишним тысячи лет назад. Другие древние народы — египтяне, вавилоняне, китайцы, народы Индии — в третьем тысячелетии до нашего летосчисления имели сведения по геометрии и арифметике, которых не хватает некоторым ученикам пятого или шестого класса. Древние египтяне были замечательными математиками и инженерами (известные всем египетские пирамиды). Ясно, что строители пирамид должны были и знать и уметь очень много! Кроме замечательных построек- пирамид, храмов и дворцов,— до нас дошли многие записи и даже большие рукописи, сделанные древними египтянами.

Понятия площадей

многоугольников:

• Равные многоугольники имеют равные площади

• Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников

• Площадь квадрата равна квадрату его стороны.

Если F1=F2 , то S(F1)=S(F2)

F1

F 2

S(F)=S(F1)+S(F2)+S(F3)

F1

F2

F3

S кв = a 2

а

Основные свойства

площадей.

Свойство №1

Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не измениться .

Доказательство: Рассмотрим ▲ ABC и ▲ ADC . Они имеют общее основание и равные высоты, так как прямые AC и BD параллельные, то расстояние между ними равно h - высоте ▲ ABC и ▲ ADC . Если площадь треугольника находится по формуле S = ah , то S ABC = S ADC = АС h

Свойство №2

Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты)

Доказательство: Пусть h 1 = h 2 в двух треугольниках с основаниями a и b .

Рассмотрим отношение площадей этих треугольников

Упростив, получим

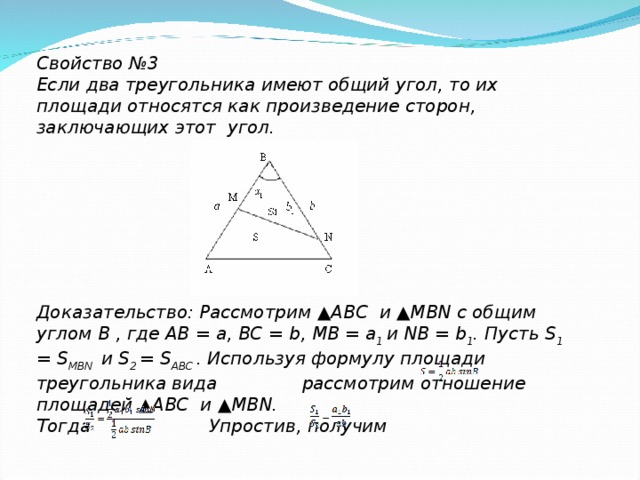
Свойство №3

Если два треугольника имеют общий угол, то их площади относятся как произведение сторон, заключающих этот угол.

Доказательство: Рассмотрим ▲ ABC и ▲ MBN с общим углом B , где AB = a , BC = b , MB = a 1 и NB = b 1 . Пусть S 1 = S MBN и S 2 = S ABC . Используя формулу площади треугольника вида рассмотрим отношение площадей ▲ ABC и ▲ MBN .

Тогда Упростив, получим

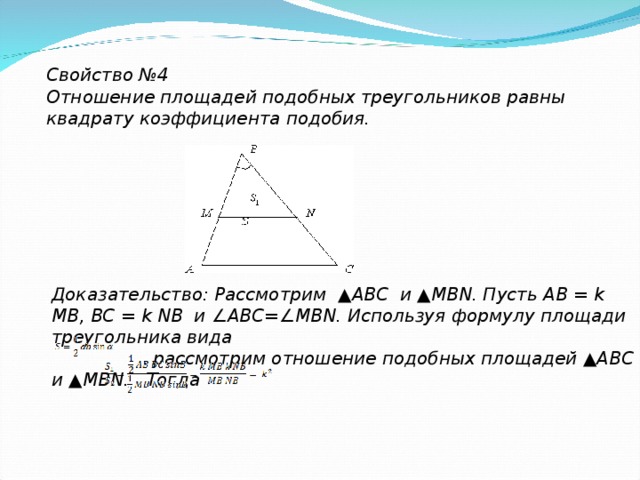
Свойство №4

Отношение площадей подобных треугольников равны квадрату коэффициента подобия.

Доказательство: Рассмотрим ▲ ABC и ▲ MBN . Пусть AB = k MB , BC = k NB и ∠ ABC =∠ MBN . Используя формулу площади треугольника вида

, рассмотрим отношение подобных площадей ▲ ABC и ▲ MBN . Тогда

Свойство № 5

Медиана треугольника делит его на две равновеликие части.

Доказательство: Рассмотрим ▲ ABC . Пусть медиана BM , тогда AM = MC = AC . Медиана делит треугольник на два с одинаковой высотой. Найдем площади треугольников ▲ ABM и ▲ MBC по формуле

Получим и . Значит S ABM = S MBC

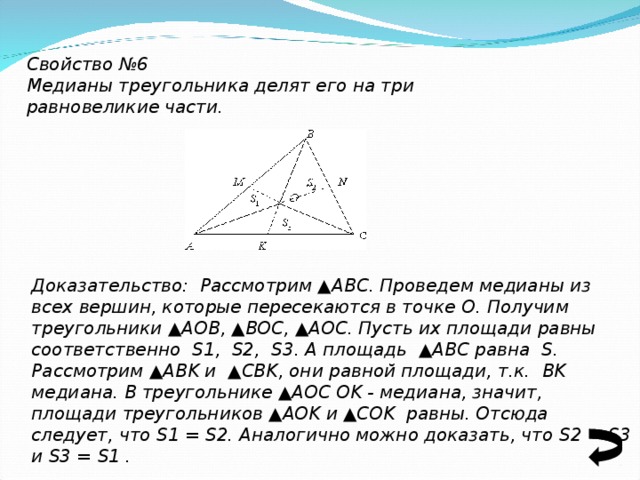
Свойство №6

Медианы треугольника делят его на три равновеликие части.

Доказательство: Рассмотрим ▲ ABC . Проведем медианы из всех вершин, которые пересекаются в точке O . Получим треугольники ▲ AOB , ▲ BOC , ▲ AOC . Пусть их площади равны соответственно S 1, S 2, S 3. А площадь ▲ ABC равна S . Рассмотрим ▲ ABK и ▲ CBK , они равной площади, т.к. BK медиана. В треугольнике ▲ AOC OK - медиана, значит, площади треугольников ▲ AOK и ▲ COK равны. Отсюда следует, что S 1 = S 2. Аналогично можно доказать, что S 2 = S 3 и S 3 = S 1 .

Свойство №7

Средние линии треугольника площади S отсекают от него треугольники площади S .

Доказательство: Рассмотрим ▲ ABC . NM - средняя линия в треугольнике и она равна половине основания AC . Если S ABC = S , то S NBM = NM h 1 = ( AC )( h )= S . Аналогично можно доказать, что площади всех треугольников равны одной четвертой части площади ▲ ABC .

Свойство №8

Медианы треугольника делят его на 6 равновеликих частей.

Доказательство: По свойству №7 площади ▲ AOB , ▲ BOC , ▲ AOC равны. По свойству №5 площади ▲ AOM , ▲ BOM равны. Значит , S1 = S6 . Аналогично , S2 = S3. Если S1 + S6 = S2 + S3 и 2S1 = 2S2 значит , S1 = S2. И так далее. получим, что все шесть треугольника имеют равные площади и они составляют шестую часть от площади ▲ ABC .

Площади многоугольников:

• Площадь прямоугольника

• Площадь параллелограмма

• Площадь треугольника

• Площадь трапеции

• Площадь ромба

Площадь прямоугольника

b

a

Дано :

Прямоугольник,

a, b - стороны,

S - площадь

Доказать :

S = ab

a

a

Доказательство:

По 3-му свойству площадь получившегося квадрата равна (а+ b ) 2 . По 2-му свойству имеем:

(а+ b ) 2 = S+S+ а 2 +b 2

а 2 +2 а b + b 2 = 2S+ а 2 +b 2 ,

отсюда получаем:

S=ab

b

b

S

b

a

Площадь параллелограмма

Дано:

ABCD – параллелограмм

Доказать: S = DK*CB

Доказательство:

1. S AECD = S ABCD + S AEB

2. S AECD = S AEKD + S DKC

Треугольник AEB = DKC

(по гипотенузе и катету),

значит, S AEB = S DKC

Отсюда следует, что площадь параллелограмма ABCD равна площади прямоугольника AE K D, т.е. равна AE ∙ AD. AE = DK , значит, S = DK*CB

D

А

К

Е

С

В

Площадь параллелограмма

B

C

A

D

B

C

O

D

A

Площадь треугольника

Дано:

∆ ABC

BH – высота

Доказать :

Доказательство:

1.Достроим ABC до параллелограмма ABDC

2 . ABC и DCB равны по трём сторонам. У них: BC – общая, AB=CD и AC=BD как противоположные стороны параллелограмма, значит, их площади равны.

3.

4.

B

D

H

C

A

Площадь треугольника

b

S =

b

a

S =

a

a

a

Площадь треугольника

1.Формула Герона:

a

b

2.

c

3.

, где P – периметр, r – радиус вписанной окружности

4.

, где R – радиус описанной окружности

S = S ABD + S BCD . 2.Примем отрезки AD и BH за основание и высоту ∆ ABD ,а отрезки BC и DH 1 за основание и высоту ∆ BCD . 3.Тогда S ABD = ½ AD*BH, S BCD = ½ BC*DH 1 , Т . к . DH 1 = BH, то S BCD = ½ BC*BH. = S = ½ AD*BH + ½ BC*BH Теорема доказана. B C H 1 A D H " width="640"

Площадь трапеции

Дано :

Трапеция А BCD ,

AD и BC – основания,

BH – высота

Доказать :

Доказательство:

1.Диагональ BD разделяет трапецию ∆ ABD и ∆ BCD = S = S ABD + S BCD .

2.Примем отрезки AD и BH за основание и высоту ∆ ABD ,а отрезки BC и DH 1 за основание и высоту ∆ BCD .

3.Тогда S ABD = ½ AD*BH, S BCD = ½ BC*DH 1 ,

Т . к . DH 1 = BH, то S BCD = ½ BC*BH.

= S = ½ AD*BH + ½ BC*BH

Теорема доказана.

B

C

H 1

A

D

H

Площадь ромба

Дано:

ABCD – ромб

AC и BD – диагонали,

О – точка пересечения диагоналей

Доказать:

Доказательство:

1.Рассмотрим прямоугольный ∆ AOB (диагонали ромба взаимно перпендикулярны)

2. ∆ AOB = ∆BOC = ∆COD = ∆ AOD , значит, их площади равны.

3.

B

О

C

A

D

Практическое применение

Система математических задач, решаемых методом площадей

Вывод:

Окружающий нас мир состоит из различного сочетания плоских и объемных фигур. В какой бы сфере не работал человек, работает ли он с природным материалом, конструирует ли различные сооружения, работает в астрономии, он должен знать свойства геометрических фигур и тел, уметь находить их объемы, площади, измерения… Эти умения и навыки необходимы человеку в его повседневной деятельности.

Знание геометрии и умение применять эти знания на практике полезно в любой профессии. Традиционно построения на местности производят геодезисты для съемки плана земельного участка, измерения его площади и строители для закладки фундаментов. Однако, знания о свойствах фигур, об их площадях бывают довольно часто нужны и в других областях деятельности: строительстве, архитектуре, геологии, агрономии и т.д.