Практическая работа №67 «Решение задач на вписанные и описанные многогранники»

Практическая работа №67 «Решение задач на вписанные и описанные многогранники»


Цель работы: сформировать умения решать задачи на вписанные и описанные многогранники в круглые тела.

Теоретические сведения к практической работе:

Вписанная и описанная призмы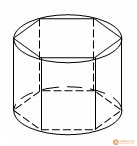  

Призмой, вписанной в цилиндр, называется такая призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковыми ребрами – образующие цилиндра. 

 

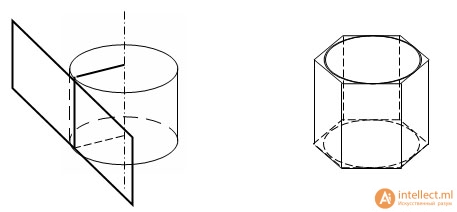Касательной плоскостью к цилиндру называется плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую. 
Призмой, описанной около цилиндра, называется призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковые грани касаются цилиндра.

Вписанная и описанная пирамиды

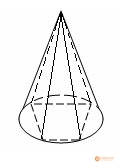
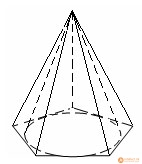
П 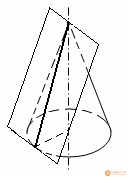ирамидой, вписанной в конус, называется такая пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершиной является вершина конуса. Боковые ребра пирамиды, вписанной в конус, являются образующими конуса. 

Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и перпендикулярная плоскости осевого сечения, содержащей эту образующую. 

 Пирамида, описанной около конуса, называется пирамида, у которой основанием служит многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса. Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса.

Вписанные и описанные многогранники

Многогранник называется вписанным в шар, если все его вершины лежат на поверхности шара.  Многогранник называется описанным около шара, если все его грани касаются поверхности шара.

Задания для самостоятельного решения:
1. В конус высотой 12 см вписана пирамида, основанием которой является прямоугольник со сторонами 6 см и 8 см. Найдите отношение площадей полных поверхностей пирамиды и конуса.
2. Диаметр шара равен 20 см. Через конец диаметра проведена плоскость под углом 45 градусов к нему. Найдите длину линии пересечения сферы этой плоскостью.
3. Диаметр шара равен 40 см. Через конец диаметра проведена плоскость под углом 30 градусов к нему. Найдите площадь сечения шара этой плоскостью.
4. В усеченный конус вписана правильная усеченная треугольная пирамида. Радиусы оснований конуса равны 2см и 5см, а высота равна 4 см. Вычислить полную поверхность пирамиды.

Контрольные вопросы:

1. Какая призма является вписанной в цилиндр?

2. Какая призма является описанной около цилиндра?

3. Какая пирамида называется вписанной в конус?

4. Какая пирамида является описанной около конуса?