Презентация к уроку по алгебре "Квадратичная функция , ее свойства и график"

Зачем мы учили это ?

• Параболой называется график функции у=х², точка О(0;0) – вершина параболы, ось О Y – ось параболы, равенство у=х² – уравнение параболы

y

O

x

Баллистическая траектория снаряда в отсутствии сопротивления воздуха при стрельбе под разным углом к горизонту.

Парабола и Космос

Если телу придать начальную скорость в пределах от 7,9 км в с до11,2 км в с, то оно на Землю не упадет, а превратится в ее спутник, движущийся по эллипсу.При скорости же 11,2 км в с тело вновь начнет двигаться по параболе и уйдет от Земли навсегда. Итак, космические корабли выходят на орбиту по параболе!

« Параболы»—аппараты с параболической формой крыла в плане.

• Б. И. Черановский предложил проект самолета типа летающего крыла с удлинением, очерченного по параболе

Параболоид вращения

• Поверхность, получаемая при вращении параболы вокруг ее оси.
• Используется для изготовления зеркал, собирающих солнечные лучи в одной точке.

Параболическая антенна

• Можно увидеть около любого аэродрома.
• Используется для того, чтобы собрать в одну точку сигналы радиолокатора, отраженные от самолета.

В прожекторах

• Свет, исходящий из фокуса параболического зеркала, после отражения образует параллельный пучок и не рассеивается. Поэтому автомобильные фары имеют форму параболоида.

Есть парабола и в телескопах

Телескоп Ньютона . Этот инструмент самый популярный у любителей вследствие легкости его изготовления (небольшой цены) и возможности применения, как для визуальных, так и для фотографических наблюдений. Главное зеркало обычно имеет форму параболы.

« Нет ни одной области математики, как бы она абстрактна не была, которая когда-нибудь не окажется применимой к явлениям действительного мира». Н.И. Лобачевский

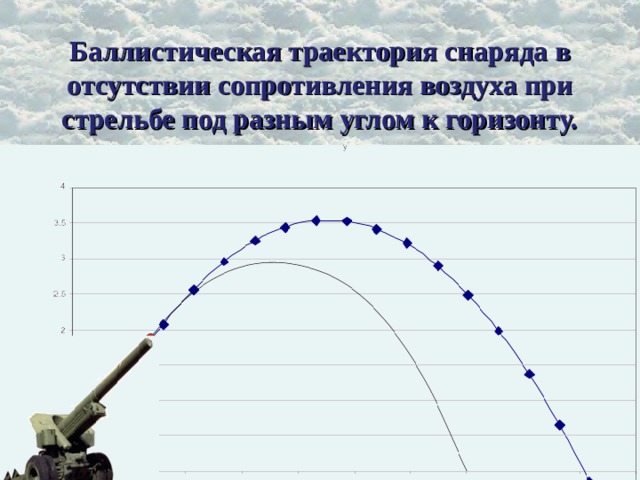
0, y .  Чему равен коэффициент a ? Как зависит положение ветвей параболы от коэффициента a ? Какое наибольшее значение функции существует и чему оно равно? Область значений функции. " width="640"

 Координаты вершины параболы.

 Уравнение оси симметрии параболы.

 Нули функции.

 Промежутки возрастания, убывания функции.

 у 0, y .

 Чему равен коэффициент a ?

• Как зависит положение ветвей параболы от коэффициента a ?
• Какое наибольшее значение функции существует и чему оно равно?
• Область значений функции.

а= -1

в= 2

с=8

у=-х 2 +2х+8

Выбери смайлик соответствующий твоему настроению:

«закипел»

«равнодушен»

«примерз»

-50 

0 

-100 

+50 

+100 