Презентации к урокам геометрии

Слайд 1 .

Усеченная пирамида.

Сопровождается музыкой. Содержит гиперссылку: «Автор и разработчик». Смена слайда – по щелчку.

Основная цель: ввести понятие конической поверхности, конуса и его элементов, вывести формулы для вычисления

площади его поверхности.

1.Актуализация опорных знаний.

2.Изучение нового материала:

а) понятие конуса,

его элементов;

б) вывод формулы площади боковой

поверхности конуса;

в) полная поверхность

конуса.

3. Это любопытно.

4. Закрепление нового материала

при решении задачи № 547, 549а.

5.Задание на дом.

6.Итоги урока.

Слайд 2.

Цель урока. Ход урока.

Содержит музыку. Открывается по щелчку.

Актуализация опорных знаний

Меню

урока

Изучение нового материала

Вывод формулы S боковой поверхности

конуса

Конические сечения.

Конус. 3D-чертеж.

Это любопытно…

Слайд 3

Меню урока

(главный управляющий слайд для перехода на другие слайды)

Сопровождается музыкой.

Содержит:

а) управляющие кнопки по щелчку, которые позволяют «открыть» нужный этап урока;

б) гиперссылку «3D-чертеж усеченной пирамиды», в которой используется фрагмент мультимедийного учебника «Стереометрия»;

В) гиперссылку «Пауза», содержащую фотографию одного из уроков (с использованием мультимедиа) по теме «Правильные многогранники» и видеоклип;

г) переход к видеофайлу по теме повторения «Пирамида», мультимедийный Flash –ролик, взятый из «Стереометрии», озвученный и преобразованный в видеофайл с помощью программы Flash to Video Encoder (взята из Интернета) ;

д) переход к историческому материалу «Это любопытно», содержащему фотографии из Интернета, фото озвучено;

е) переход к формулам площадей многоугольников, которые необходимы при вычислении площадей оснований усеченной пирамиды.

Итоги урока

Пауза

Исторические сведения

Формулы площадей

Пауза

3

2

1

5

4

9

7

8

6

Слайд 4.

Актуализация знаний.

Переход к следующему слайду – по щелчку.

Содержит управляющую кнопку «Меню урока» и управляющие кнопки в ответе к заданию №1, после нажатия на них выдается сообщение о правильности решения данного задания.

• Среди изображенных тел выберите номера тех,

которые являются конусом.

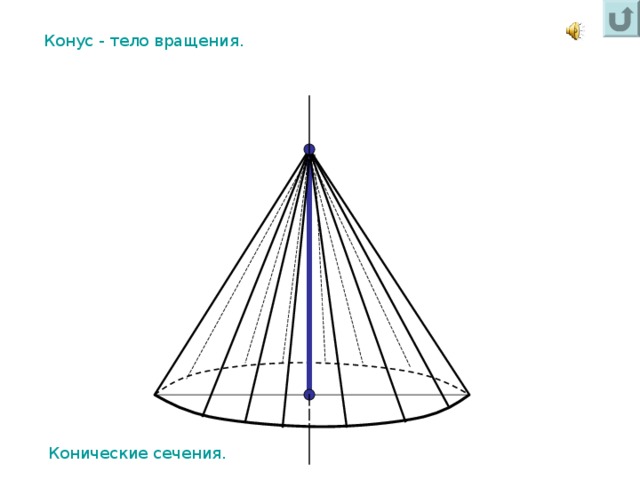
Конус - тело вращения.

P

O

L

Конические сечения.

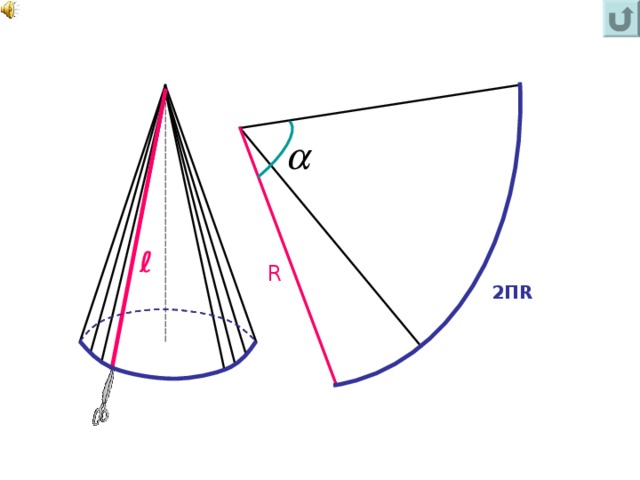
За площадь боковой поверхности конуса принимается площадь её развертки:

Р

А 1

Р

ℓ

R

2ПR

В

А

В

А

Выведем площадь боковой поверхности конуса.

Меню урока

S бок = π R ℓ;

S кон = π R(ℓ + R)

Меню урока

Итоги урока:

• Конусом называется тело …
• Высотой конуса называется ….

• Площадью полной поверхности конуса называется …
• За площадь боковой поверхности конуса принимается …
• Осевым сечением конуса является…

• Площадь боковой поверхности конуса равна…
• Площадь полной поверхности конуса равна …
• Площадь круга равна …
• Конус получается вращением …

Конус.3-Dчертёж.

Слайд 5.

Продолжите предложения.

Содержит гиперссылки «Пирамида 3D-чертеж» и «Правильная пирамида 3D-чертеж» для проверки правильности устного ответа учащихся.

Конус - тело вращения

Формулы

площадей

Слайд 23.

Формулы площадей многоугольников.

Содержит 4 гиперссылки:

Параллелограмм

Треугольник

Трапеция

Ромб.

После просмотра – возврат в меню урока.

Треугольник

Круг

Меню урока

Меню урока

Площадь треугольника.

a 2 √3

S =

a

a

4

где а - сторона

равностороннего треугольника

a

Слайды 24-27.

Нужны для повторения формул площадей основных многоугольников, лежащих в основаниях усеченной пирамиды.

Управляющая кнопка возврата возвращает к слайду 23 «Формулы площадей многоугольников.

S = ½ a b ,

а, b - катеты прямоугольного треугольника

b

a

Площадь круга:

R

R 2

S =

Меню урока

Из истории.

Понятие конической поверхности было введено Апполонием в его «Конических сечениях», при этом он имел ввиду обе полости конуса. Вот что пишет Апполоний: «Если от какой-либо точки окружности Круга, который не находится в одной плоскости с некоторой точкой,

Проводить прямые, соединяющие эту точку с окружностью, и при неподвижности точки перемещать прямую по окружности, возвращая её туда, откуда началось движение, то поверхность, описанную прямой и составленную из двух поверхностей, лежащих в вершине друг против друга,

из которых каждая бесконечно увеличивается, если бесконечно продолжать описывать прямую, я называю конической поверхностью, неподвижную же точку – её вершиной, а осью – прямую, проведенную через эту точку и центр круга».

Определение конической поверхности Апполония воспроизведено в современных школьных учебниках с существенной заменой круга на Любую линию, так называемую направляющую.

Площадь боковой поверхности конуса была найдена Архимедом . В 14-м предложении его произведения «О шаре и цилиндре» он доказывает следующую теорему: «Поверхность всякого равнобедренного (т.е прямого кругового) конуса, за вычетом основания, равна кругу, радиус которого есть средняя пропорциональная между стороной (т.е образующей) конуса и радиусом

круга, являющегося основанием конуса»

Меню урока

АРХИМЕД (ок. 287–212 до н.э.),

величайший древнегреческий математик и механик.

Уроженец греческого города Сиракузы на острове Сицилия

Алгоритм рассуждений:

Площадь кругового сектора:

Р

S = ℓ 2

Чему равна длина окружности ?

Выразите ℓ через r.

R

О

А