Пояснительная записка
Календарно тематическое планирование по алгебре для 8 класса составлено на основе
- федерального государственного образовательного стандарта основного общего образования;
- требований к результатам освоения основной образовательной программы основного общего образования;
- примерной программы основного общего образования по математике 5 – 9 классы / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е. В. Буцко.
Учебник алгебра 8 классА.Г. Мерзляк, В.М.Полонский – углубленный уровень. Издательский центр «Вентана-Граф», 2019
Календарно тематическое планирование рассчитано на 2 часа в неделю согласно расписанию уроков и приказу директора.
С 02.12.2019г по 17.01.2020г.
При составлении данной рабочей программы были учтены требования официальных нормативных документов:
Федеральный закон от 29.12.2012 г. №273-ФЗ «Об образовании в РФ»;
Приказ Министерства образования РФ от 17.12.2010 г. №1897, зарегистрированный Минюстом России 1 февраля 2011 г. №19644, «Об утверждении федерального государственного образовательного стандарта основного общего образования.
Приказ Министерства образования РФ от 29 декабря 2014 г. №1644 «О внесении изменений в приказ Министерства образования и науки РФ от 17 декабря 2010 г.№1897 «Об утверждении ФГОС основного общего образования»;
Приказ Минобрнауки России от 31.12.2015 №1577 «О внесении изменений в федеральный государственный стандарт основного общего образования, утвержденный приказом Министерства образования и науки Российской Федерации» от 17 декабря 2010г. №1897.
Примерная основная образовательная программа основного общего образования, одобренная Федеральным учебно-методическим объединением по общему образованиию (протокол заседания от 08 апреля 2015 №1/15);
Постановление Главного государственного санитарного врача Российской Федерации от 29 декабря 2010 г. № 189 «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» (ред. Постановления Главного государственного санитарного врача РФ от 24.11.2015 №81).
Письмо Департамента государственной политики в сфере образования Минобрнауки России от 28.10.2015 №08-1786 «О рабочих программах учебных предметов».
Приказ Минобрнауки России от 31.03.2014 №253 «Об утверждении федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования» (ред. приказа Минобрнауки России от 05.07.2017. №629).
Письмо Рособрнадзора от 20.06. 2018 №05-192 «О реализации прав на изучение родных языков из числа языков народов РФ в общеобразовательных организациях»
Содержание и методический аппарат программы способствуют формированию у учащихся личностных, метапредметных, предметных результатов обучения.
Личностные результаты формируют:
1) Воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, знание истории, культуры своего народа, основ культурного наследия народов России и человечества.
2) Ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, осознанному выбору и построению дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к труду, развития опыта участия в социально значимом труде.
3) Формирование осознанного, уважительного и доброжелательного отношения к другому человеку, его мнению, мировоззрению, культуре, к истории, традициям, ценностям народов России и народов мира; готовности и способности вести диалог с другими людьми и достигать в нём взаимопонимания.
4) Развитие компетентности в области использования информационно-коммуникационных технологий.
Предметные результаты формируют:
1) Осознание значения математики для повседневной жизни человека. Формирование представлений о математике как о методе познания действительности, позволяющем описывать и изучать реальные процессы и явления.
2) Развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования, доказательства математических утверждений.
3) Овладение символьным языком алгебры, приёмами выполнения тождественных преобразований выражений, решения уравнений, систем уравнений, неравенств и систем неравенств.
4) Развитие умений применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин; умения моделировать реальные ситуации на языке алгебры.
5) Овладение системой функциональных понятий, развитие умения использовать функционально-графические представления для решения различных математических задач, для описания и анализа реальных зависимостей.
ОБЩАЯ ХАРАКТЕРИСТИКА КУРСА
Для дальнейшей работы в области теоретической и прикладной математики и технических дисциплин необходимо развить у учащихся навыки формально-логического мышления, сформировать потребность в доказательстве математических фактов, обеспечить сознательное усвоение математических знаний и причинно-следственных связей в изучаемом курсе, заложить основы математического мышления и математической культуры, научить использовать полученные знания для творческого решения проблем и применять их в нестандартных ситуациях. Способность учащегося усваивать курс математики, построенных на данных принципах, является одним из факторов, позволяющих ему убедиться в правильности выбора своего направления специализации. Исходя из этих требований и принципов, данная программа построена с преобладанием формально-логического подхода; естественно-дедуктивный принцип играет второстепенную, в основном иллюстративную и эмоциональную роль, способствующую интериоризации знаний. Учитывая то, что в массовой школе использование формально-логического метода построения курса математики практически невозможно, много внимания уделяется переходу от наглядно-дедуктивного принципа изложения к формально- логическому и выработке у учащихся соответствующих навыков мышления, что закладывает основы для дальнейшего углублённого курса математики в старших классах.
В то же время необходимо учитывать возрастные особенности мышления учащихся, использовать разнообразные приёмы повышения эффективности усвоенного материала. Например, графическое представление объектов, схемы их классификации. Для наглядного представления иерархичных отношений множеств объектов широко используются схемы, построенные по принципу диаграмм Эйлера. Изучение свойств объектов обобщается в виде таблиц. При изучении функциональных зависимостей важно установление соответствия между свойствами функции и свойствами её графика. Необходимо уделять значительное внимание формированию у учащихся навыков работы с графическими изображениями функциональных зависимостей.
МЕСТО АЛГЕБРЫ В УЧЕБНОМ ПЛАНЕ
Рабочая программа рассчитана на 11 часов (2 часа в неделю).
ТРЕБОВАНИЯ К РЕЗУЛЬТАТАМ ОБУЧЕНИЯ
1) в личностном направлении:
• умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
• критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
• представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
• креативность мышления, инициатива, находчивость, активность при решении математических задач;
• умение контролировать процесс и результат учебной математической деятельности;
• способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
2) в метапредметном направлении:
• первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;
• умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
• умение находить в различных источниках информацию, необходимую для решения математических проблем, представлять ее в понятной форме, принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
• умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
• умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки;
• умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
• понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
• умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
• умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
3) в предметном направлении:
усвоил математические знания, предусмотренные программой, в их логической последовательности и взаимосвязи,
формулирует и обосновывает соответствующие теоретические положения и умеет применять их к решению задач и выполнению практических заданий;
логически мыслит (анализирует, сравнивает, обобщает и систематизирует, классифицирует математические объекты по определённым свойствам, приводит примеры и контрпримеры, выдвигает и проверяет гипотезы); владеет алгоритмами и эвристиками;
определяет математический аппарат, необходимый для решения конкретной задачи, составляет алгоритм решения задачи и решает её, пользуясь приобретенными знаниями;
выполняет математические расчёты (действия с числами, представленными в различных формах, действия с процентами, приближённые вычисления и т. п.), рационально сочетая устные, письменные, инструментальные вычисления;
выполняет тождественные преобразования алгебраических выражений при решении различных задач;
анализирует графики функциональных зависимостей, исследует их свойства, использует свойства элементарных функций для анализа и описания реальных явлений, физических процессов, зависимостей;
вычисляет вероятности случайных событий, оценивает шансы их наступления, выбирает оптимальные решения;
успешно применяет полученные знания в прикладном аспекте, применяет математические модели при изучении окружающего мира, в частности, в курсе физики и других учебных предметов (информатики, астрономии, экономики и т. д.), распознаёт задачи, которые можно решить с помощью математических методов, формулирует их на математическом языке, исследует и решает эти задачи, используя математические знания и методы,
интерпретирует полученные результаты с учётом конкретных условий и целей исследования, выполняет статистическую обработку полученных результатов;
пользуется источниками математической информации, может самостоятельно её найти, представить информацию в различных формах (графической, табличной, знаково-символьной) и проанализировать её;
на основании рассмотренных выше знаний и умений разрабатывает соответствующие математические модели, составляет постановку задачи и алгоритмы для создания компьютерных программ и компьютерной обработки информации
Цели и задачи курса:
Цель изучения алгебры в классах с углублённым изучением математики состоит в обеспечении уровня подготовки учащихся по математике, необходимого для успешной самореализации личности в динамической социальной среде. Для дальнейшего выбора и успешного освоения профессии, требующей высокого уровня математических знаний, то есть специализации в направлении теоретической и прикладной математики либо в областях, требующих развитого математического аппарата для изучения и анализа закономерностей реальных явлений и процессов; в подготовке к обучению в высшем учебном заведении соответствующего профиля.
Достижение указанных целей обеспечивается выполнением соответствующих задач:
формирование у учащихся представления о роли математики в познании действительности, о математических знаниях как неотъемлемой составляющей общей культуры человека, необходимого условия полноценной жизни в современном обществе и аппарате научного познания;
создание стойкой позитивной мотивации к обучению;
формирование у учащихся стойкого интереса к предмету, выявление и развитие математических способностей;
формирование у учащихся научного мировоззрения, представления о формально-логическом построении системы математических знаний, идеях и методах математики, потребности в обосновании и формальном доказательстве математических знаний и фактов;
интеллектуальное развитие личности, в первую очередь развитие у учащихся логического мышления и пространственного представления, алгоритмической, информационной и графической культуры, памяти, внимания, интуиции;
овладение учащимися системой математических знаний, навыков и умений, необходимых в будущей профессиональной деятельности с учетом ориентации учащихся на специализацию в областях, требующих углублённого изучения математики;
усвоение современного математического моделирования («языка математики») в устной и письменной формах;
приобретение математических знаний в их диалектическом единстве с другими научными дисциплинами, изучаемыми в общеобразовательной школе, установление межпредметных связей;
гражданское, экологическое, эстетическое воспитание и формирование позитивных черт личности, формирование жизненных и социально-ценностных компетенций учащегося.
Одной из главных целей изучения алгебры в 8 классе является содействие развитию у учащихся интереса к углублённому изучению предмета и постепенное вовлечение учащихся в повышенный объем работы над предметом по сравнению с учащимися общеобразовательных классов.
Также необходимо учитывать то, что учащийся может пересмотреть свой выбор и вернуться к обучению в общеобразовательном классе. Исходя из этого, программа построена по принципу согласования материала и учебного плана с соответствующими программами общеобразовательных классов.
ФОРМЫ И СРЕДСТВА КОНТРОЛЯ
Основными методами проверки знаний и умений учащихся по математике являются устный опрос и письменные работы. К письменным формам контроля относятся: математические диктанты, самостоятельные и контрольные работы, тесты. Основные виды проверки знаний – текущая и итоговая. Текущая проверка проводится систематически из урока в урок, а итоговая – по завершении темы (раздела), школьного курса. Для проведения контрольных и самостоятельных работ, тестов используется Алгебра. 8 класс. Углублённое изучение. Самостоятельные и контрольные работы. ФГОС, Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. .- М.:Вентана-Граф, 2016.
СОДЕРЖАНИЕ ОБУЧЕНИЯ.
Неравенства (2 часа): Числовые промежутки: Интервал, отрезок, луч. Неравенство с одной переменной. Решение неравенств. Линейные неравенства с одной переменной и их системы. Квадратные неравенства. Дробно – рациональные неравенства. Неравенства, содержащие переменную под знаком модуля.
Квадратные корни. Действительные числа. (11 часов): Функция у=х2 и её график. Бесконечная десятичная дробь как результат измерения отрезка. Действительные числа как бесконечные десятичные дроби. Периодические десятичные дроби. Примеры бесконечных непериодических десятичных дробей. Свойства множества действительных чисел. Интервальный ряд данных.
Решение уравнения х2 = 2 во множестве рациональных чисел и во множестве действительных чисел.
Квадратный корень из числа. Условие существования квадратного корня и число квадратных корней из действительного числа. Арифметический квадратный корень. Свойства квадратных корней и их применение в вычислениях.
Понятие об иррациональном числе. Иррациональность числа 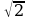 . Десятичные приближения иррациональных чисел. Нахождение приближенного значения корня с помощью калькулятора. График функции у =
. Десятичные приближения иррациональных чисел. Нахождение приближенного значения корня с помощью калькулятора. График функции у = 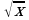 . Дробно – линейная функция и ее график.
. Дробно – линейная функция и ее график.
Требования к уровню подготовки
Алгебраические выражения
Ученик должен научится:
• оперировать понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами;
• выполнять преобразования выражений, содержащих степени с целыми показателями и квадратные корни;
• выполнять тождественные преобразования рациональных выражений на основе правил действий над алгебраическими дробями;
• выполнять разложение квадратного трехчлена на множители.
Уравнения
Ученик должен научится:
• решать основные виды рациональных уравнений с одной переменной;
• понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
• применять графические представления для исследования уравнений.
Числовые функции
Ученик должен научится:
• понимать и использовать функциональные понятия и язык (термины, символические обозначения);
• строить графики элементарных функций у=к/х; у=х2; у=√х; исследовать свойства числовых функций на основе изучения поведения их графиков;
• понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Числовые множества
Выпускник должен научится:
• понимать терминологию и символику, связанные с понятием множества, выполнять операции над множествами;
• использовать начальные представления о множестве действительных чисел.
Метапредметные:
1)умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе, развивать мотивы и интересы своей познавательной деятельности;
2)умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения
результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
3)умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
4)умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
5)развитие компетентности в области использования информационно-коммуникационных технологий.
6)первоначальные представления об идеях и о методах математики как об универсальном языке науки и технике, о средстве моделирования явлений и процессов;
7)умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
8)умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме, принимать решение в условиях неполной или избыточной, точной или вероятностной информации;
9)умение понимать и использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации.
10)умение выдвигать гипотезы при решении задачи понимать необходимость их проверки;
11)понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Личностные:
воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;
ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;
умение контролировать процесс и результат учебной и математической деятельности;
критичность мышления, инициатива, находчивость, активность при решении математических задач.
Календарно тематическое планирование по алгебре
8 класс
| Изучаемый материал | Кол-во часов | Дата изучения |
| план | факт |
| Глава IV. Неравенства |
|
|
|
| Уравнения и неравенства, содержащие знак модуля. | 1 | 02.12.2019 | 02.12.2019 |
| Уравнения и неравенства, содержащие знак модуля. | 1 | 04.12.2019 | 04.12.2019 |
| Глава V. Квадратные корни. Действительные числа. |
|
|
|
| Функция у =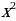 и её график. и её график. | 1 | 09.12.2019 | 09.12.2019 |
| Функция у =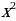 и её график. и её график. | 1 | 11.12.2019 | 11.12.2019 |
| Квадратные корни. Арифметический квадратный корень. | 1 | 16.12.2019 | 16.12.2019 |
| Квадратные корни. Арифметический квадратный корень. | 1 | 18.12.2019 | 18.12.2019 |
| Множество действительных чисел. | 1 | 23.12.2019 | 23.12.2019 |
| Множество действительных чисел. | 1 | 25.12.2019 | 25.12.2019 |
| Свойства арифметического квадратного корня | 1 | 30.12.2019 | 30.12.2019 |
| Свойства арифметического квадратного корня | 1 | 13.01.2020 | 13.01.2020 |
| Свойства арифметического квадратного корня | 1 | 15.01.2020 | 15.01.2020 |
Литература и средства обучения
Алгебра: 8 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – М.: Вентана –Граф, 2015.
Алгебра: 8 класс: дидактические материалы: сборник задач и контрольных работ/ А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – М.: Вентана –Граф, 2015.
Алгебра : 8 класс: методическое пособие / Е.В. Буцко, А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – М.: Вентана –Граф, 2015
Справочные пособия, научно-популярная и историческая литература:
Агаханов Н.Х., Подлипский O.K. Математика: районные олимпиады: 6-11 классы. — М.: Просвещение, 1990.
Гаврилова Т.Д. Занимательная математика: 5-11 классы. — Волгоград: Учитель, 2008.
Левитас Г.Г. Нестандартные задачи по математике. — М.: ИЛЕКСА, 2007.
Перли С.С., Перли Б.С. Страницы русской истории на уроках математики. — М.: Педагогика-Пресс, 1994.
Пичугин Л.Ф. За страницами учебника алгебры. — М.: Просвещение, 2010.
Пойа Дж. Как решать задачу? — М.: Просвещение, 1975,-
Произволов В.В. Задачи на вырост. — М.: МИРОС, 1995,
Фарков А.В. Математические олимпиады в школе : 5- 11 классы. — М. : Айрис-Пресс, 2005.
Энциклопедия для детей. Т. 11: Математика. — М.: Аванта-+, 2003.
http://www.kvant.info/ Научно-популярный физико-математический журнал для школьников и студентов «Квант».
12







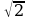 . Десятичные приближения иррациональных чисел. Нахождение приближенного значения корня с помощью калькулятора. График функции у =
. Десятичные приближения иррациональных чисел. Нахождение приближенного значения корня с помощью калькулятора. График функции у = 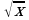 . Дробно – линейная функция и ее график.
. Дробно – линейная функция и ее график.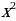 и её график.
и её график.









