СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока


Рабочая программа
В данной работе представлена рабочая программа по математики для студентов техникума
Просмотр содержимого документа
«Рабочая программа»
Министерство образования и науки Республики Бурятия
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«БУРЯТСКИЙ РЕСПУБЛИКАНСКИЙ ТЕХНИКУМ СТРОИТЕЛЬНЫХ И ПРОМЫШЛЕННЫХ ТЕХНОЛОГИЙ»
Рабочая ПРОГРАММа
общеобразовательной УЧЕБНОЙ ДИСЦИПЛИНЫ «математика»
для профессий
среднего специального образования
19.01.17 «Повар, кондитер»
г.Кяхта, 2016
Рабочая программа разработана с учетом требований ФГОС среднего общего образования, ФГОС среднего профессионального образования по профессиям 19.01.17 «Повар, кондитер»
Организация-разработчик: ГБПОУ «Бурятский Республиканский техникум строительных и промышленных технологий».
Разработчик: Цыдыпова Татьяна Сергеевна, преподаватель математики.
Рассмотрена на ЦК общеобразовательных дисциплин, протокол № ___от ______20____ г.
Председатель ЦК Цыдыпова Т.С /______________/
Утверждена заместителем директора по учебной работе: Бурантарова Е.А. /_____________/
«______»______________ 20____г.
| | стр. |
| 4 |
| 4 |
| 5 |
| 5 |
| 7 |
| 16 |
| 23 |
| 24 |
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Общеобразовательная учебная дисциплина «Математика: алгебра и начала математического анализа; геометрия» (далее – «Математика») изучается в ГБПОУ «БРТСиПТ» на базе основного общего образования при подготовке квалифицированных рабочих, служащих по профессии 19.01.17 «Повар, кондитер»
Программа разработана на основе примерной программы общеобразовательной дисциплины «Математика», одобренной научно-методическим советом Центра профессионального образования ФГАУ «ФИРО» и рекомендованной для реализации основной профессиональной образовательной программы СПО на базе основного общего образования с получением среднего общего образования (Протокол № 3 от 21 июля 2015 г.), с учетом требований федеральных государственных образовательных стандартов и получаемой профессии среднего профессионального образования.
Содержание программы «Математика» направлено на достижение следующих целей:
обеспечения сформированности представлений о социальных, культурных и исторических факторах становления математики;
обеспечения сформированности логического, алгоритмического и математического мышления;
обеспечения сформированности умений применять полученные знания при решении различных задач;
обеспечения сформированности представлений о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления.
В программу включено содержание, направленное на формирование у студентов компетенций, необходимых для качественного освоения ОПОП СПО на базе основного общего образования с получением среднего общего образования – программы подготовки квалифицированных рабочих, служащих, программы подготовки специалистов среднего звена (ППКРС, ППССЗ).
Срок реализации программы: 2 года
ОБЩАЯ ХАРАКТЕРИСТИКА УЧЕБНОЙ ДИСЦИПЛИНЫ
«Математика: алгебра и начала математического анализа; геометрия»
Математика является фундаментальной общеобразовательной дисциплиной со сложившимся устойчивым содержанием и общими требованиями к подготовке обучающихся.
При освоении профессий СПО математика изучается на базовом уровне ФГОС среднего общего образования при освоении профессий СПО и специальностей СПО.
Общие цели изучения математики традиционно реализуются в четырех направлениях – общее представление об идеях и методах математики, интеллектуальное развитие, овладение необходимыми конкретными знаниями и умениями, воспитательное воздействие.
Содержание учебной дисциплины разработано в соответствии с основными содержательными линиями обучения математике:
– алгебраическая линия, включающая систематизацию сведений о числах; изучение новых и обобщение ранее изученных операций (возведение в степень, извлечение корня, логарифмирование, синус, косинус, тангенс, котангенс и обратные к ним); изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и прикладных задач;
– теоретико-функциональная линия, включающая систематизацию и расширение сведений о функциях, совершенствование графических умений; знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи;
– линия уравнений и неравенств, основанная на построении и исследовании математических моделей, пересекающаяся с алгебраической и теоретико-функциональной линиями и включающая развитие и совершенствование техники алгебраических преобразований для решения уравнений, неравенств и систем; формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных и специальных дисциплин;
– геометрическая линия, включающая наглядные представления о пространственных фигурах и изучение их свойств, формирование и развитие пространственного воображения, развитие способов геометрических измерений, координатного и векторного методов для решения математических и прикладных задач;
– стохастическая линия, основанная на развитии комбинаторных умений, представлений о вероятностно-статистических закономерностях окружающего мира.
В тематическом плане программы учебный материал представлен в форме чередующегося развертывания основных содержательных линий (алгебраическая, теоретико-функциональная, уравнений и неравенств, геометрическая, стохастическая), что позволяет гибко использовать их расположение и взаимосвязь, составлять рабочий календарный план, по-разному чередуя учебные темы (главы учебника.
Изучение общеобразовательной учебной дисциплины «Математика» завершается подведением итогов в форме экзамена в рамках промежуточной аттестации студентов в процессе освоения основной ОПОП СПО с получением среднего общего образования (ППКРС, ППССЗ).
В ходе изучения теоретического материала проводятся контрольные и самостоятельные работы. Обучающиеся занимаются выполнением исследовательских работ самостоятельно.
Итоговая аттестация по учебной дисциплине проводится в форме письменного экзамена.
МЕСТО УЧЕБНОЙ ДИСЦИПЛИНЫ В УЧЕБНОМ ПЛАНЕ
Учебная дисциплина «Математика: алгебра и начала математического анализа; геометрия» изучается в общеобразовательном цикле учебного плана ППКРС СПО на базе основного общего образования с получением среднего общего образования.
РЕЗУЛЬТАТЫ ОСВОЕНИЯ ДИСЦИПЛИНЫ
Освоение содержания учебной дисциплины «Математика» обеспечивает достижение студентами следующих результатов:
личностных:
- сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
- понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;
- развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;
- овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественнонаучных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;
- готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
- готовность и способность к самостоятельной, творческой и ответственной деятельности;
- готовность к коллективной работе, сотрудничеству со сверстниками в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;
- отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;
метапредметных:
- умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;
- умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;
- владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;
- готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;
- владение языковыми средствами – умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;
- владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств их достижения;
- целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира;
предметных:
- сформированность представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;
- сформированность представлений о математикеческих понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
- владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач;
- владение стандартными приёмами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;
- сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;
- владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать на чертежах, моделях и в реальном мире геометрические фигуры; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;
- сформированность представлений о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;
- владение навыками использования готовых компьютерных программ при решении задач.
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ
5.1.СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ
| Виды учебной деятельности | Объем часов технического профиля |
| Максимальная учебная нагрузка | 341 |
| Обязательная аудиторная учебная нагрузка (всего) | 228 |
| в том числе: |
|
| практическая часть | 127 |
| контрольные работы | 19 |
| Самостоятельная работа обучающегося (всего) | 113 |
| в том числе: |
|
| -Выполнение домашнего задания: систематическая проработка конспектов занятий; - Изготовление наглядных моделей - Реферат, сообщение Подготовка к: - практическим и самостоятельным работам - тематическим контрольным работам - зачетам. | 63 5 15 11 19 |
| Промежуточная аттестация в виде контрольной работы (тестовые задания с выбором ответов, задания с приведением решения), письменного экзамена. | |
| 5.2. ТЕМАТИЧЕСКИЙ ПЛАН И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- ХАРАКТЕРИСТИКА ОСНОВНЫХ ВИДОВ ДЕЯТЕЛЬНОСТИ СТУДЕНТОВ
| Содержание обучения | Характеристика основных видов деятельности обучающегося (на уровне учебных действий) |
|
| ВВЕДЕНИЕ |
| Введение |
|
|
| АЛГЕБРА |
| Развитие понятия о числе
|
|
| Корни, степени, логарифмы
|
инструментальные средства
|
| Преобразование алгебраических выражений
|
| ||
| ОСНОВЫ ТРИГОНОМЕТРИИ | |||
| Основные понятия
|
| ||
| Основные тригонометрические тождества |
| ||
| Преобразования простейших тригонометрических выражений
|
| ||
| Простейшие тригонометрические уравнения и неравенства
|
| ||
| Арксинус, арккосинус, арктангенс числа |
| ||
| ФУНКЦИИ, ИХ СВОЙСТВА И ГРАФИКИ | |||
| Функции Понятие о непрерывности функции
|
| ||
| Свойства функции. Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях
|
| ||
| Обратные функции
|
| ||
| Степенные, показательные, логарифмические и тригонометрические функции. Обратные тригонометрические функции |
| ||
| НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА | |||
|
|
| ||
| Производная и ее применение
|
| ||
| Первообразная и интеграл |
| ||
| УРАВНЕНИЯ И НЕРАВЕНСТВА | |||
| Уравнения и системы уравнений Неравенства и системы неравенств с двумя переменными
|
Решать неравенства и системы неравенств, применяя различные способы.
| ||
| ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, ТЕОРИИ ВЕРОЯТНОСТЕЙ И СТАТИСТИКИ | |||
| Основные понятия комбинаторики |
| ||
| Элементы теории вероятностей |
| ||
| Представление данных (таблицы, диаграммы, графики) |
| ||
|
| ГЕОМЕТРИЯ | ||
| Прямые и плоскости в пространстве
|
Изображать на чертежах и моделях расстояния и обосновывать свои суждения. Определять и вычислять расстояния в пространстве. Применять формулы и теоремы планиметрии для решения задач.
| ||
| Многогранники |
| ||
| Тела и поверхности вращения
|
| ||
| Измерения в геометрии
|
| ||
| Координаты и векторы |
Изучить декартову систему координат в пространстве, строить по заданным координатам точки и плоскости, находить координаты точек.
| ||
УЧЕБНО-МЕТОДИЧЕСКОЕ И МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ
Учебно-методическое обеспечение
Учебно-методический комплекс:
1. Алгебра и начала математического анализа.10-11классы. В 2ч. Ч.2. Задачник для учащихся общеобразовательных учреждений (базовый уровень) / [А.Г.Мордкович и дл.] под ред. А.Г.Мордковича.-10-у изд., стер.-М.:Мнемозина,2014.-239 с.: ил.
2. Мордкович А.Г. Алгебра и начала математического анализа.10-11классы. В 2ч. Ч.1. Задачник для учащихся общеобразовательных учреждений (базовый уровень)/ А.Г.Мордкович.10-е изд., стер.- М.: Мнемозина, 2014г.-399 с.: ил.
3. Контрольно-измерительные материалы. Сборник заданий и математических диктантов по математике.
4. Геометрия, 10-11: учеб. для общеобразоват. учреждений / [Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.]-15-е изд., доп. – М.: Просвещение, 2006. – 256 с.: ил.
Учебно-методические пособия: Методические рекомендации по выполнению внеаудиторной самостоятельной работы и по выполнению практической работы.
Нормативные документы дисциплины: рабочая программа дисциплины, паспорт кабинета, инструкции по технике безопасности, календарно-тематический план дисциплины.
Электронно-образовательные ресурсы:
Башмаков М. И. Математика: учебник для учреждений нач. и сред. проф. образования / М. И. Башмаков. – 7-е изд., стер. – М.: Издательский центр «Академия», 2013. – 256 с.
Башмаков М. И. Математика: учебник / М. И. Башмаков. – М.: КНОРУС, 2013. – 400 с. – (Начальное и среднее профессиональное образование).
Данко П.Е. Высшая математика.
Ершова А.П., Голобородько В.В. «Самостоятельные и контрольные работы по алгебре и началам анализа», 205с.
Методические рекомендации и пособия по математике по выполнению внеаудиторной СРС.
Презентации к урокам математики.
Материально-техническое обеспечение
Для реализации данной программы имеется учебный кабинет, оборудованный рабочим местом преподавателя, 30 посадочными местами для обучающихся и мультимедийным оборудованием и наглядно-демонстрационными пособиями.
Мультимедийное оборудование:
компьютер - 1 шт.
принтер - 1 шт.
экран – 1 шт.
Проектор – 1 шт.
Наглядно-демонстрационные пособия:
комплекты таблиц, плакатов, карт, справочных пособий.
комплект учебно-наглядных пособий «Математика»;
комплект моделей стереометрических фигур (демонстрационный);
комплект моделей стереометрических фигур (раздаточный);
комплект измерительных инструментов: линейка, транспортир, угольник, циркуль.
ЛИТЕРАТУРА
Основные источники:
1. Алгебра и начала математического анализа.10-11классы. В 2ч. Ч.2. Задачник для учащихся общеобразовательных учреждений (базовый уровень) / [А.Г.Мордкович и дл.] под ред. А.Г.Мордковича.-10-у изд., стер.-М.:Мнемозина,2014.-239 с.: ил.
2. Мордкович А.Г. Алгебра и начала математического анализа.10-11классы. В 2ч. Ч.1. Задачник для учащихся общеобразовательных учреждений (базовый уровень)/ А.Г.Мордкович.10-е изд., стер.- М.: Мнемозина, 2014г.-399 с.: ил.
3. Погорелов А.В. Геометрия: Учеб. для 7 – 11 кл. общеобразоват. учреждений. – 9 –е изд. – М.: Просвещение, 2011г. – 383 с.: ил.
Дополнительные источники:
1. Алгебра и начала анализа: учеб. для 10-11 кл. общеобразоват. учреждений / [Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров и др.].-131-е изд.-М.: Просвещение, 2006.-384с.:ил.
2. Башмаков М.И.. Алгебра и начала анализа. 10 – 11 кл. Учеб. для общеобразоват. учеб. заведений. – 4-е изд., стереотип. – М.: Дрофа, 2006. – 400 с.: ил.
3. Геометрия, 10-11: учеб. для общеобразоват. учреждений / [Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.]-15-е изд., доп. – М.: Просвещение, 2006. – 256 с.: ил.
4. Колмогоров А.Н. Алгебра и начала анализа. 10- 11. Просвещение.2009.
5. Тульчинская Е.Е., Мордкович А.Г. Алгебра и начала анализа. 10-11 классы: контрольные работы: учебное пособие.- М.:Мнемозина,2007.
6. http://lineyka.inf.ua/-LINEYKA.INF.UA–МАТЕМАТИЧЕСКИЙ ПОРТАЛ.


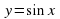 , ее свойства и график
, ее свойства и график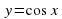 , ее свойства и график
, ее свойства и график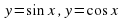
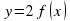 , если есть график функции
, если есть график функции 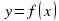
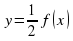 , если есть график функции
, если есть график функции 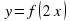 , если есть график функции
, если есть график функции 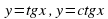 , их свойства и графики
, их свойства и графики
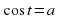
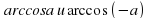
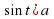
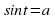 . Частные случаи
. Частные случаи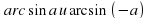
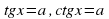
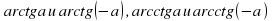 .
.