План-конспект урока по алгебре в 7 классе.
Разложение на множители суммы и разности кубов.
Дата_____________
Форма урока: комбинированный.
Цели урока:
Образовательные:
• научиться раскладывать на множители сумму и разность кубов.
• закрепить и проверить уровень знаний, умений и навыков применения формул сокращенного умножения;
• усовершенствовать навыки решения текстовых задач, использующих операции над числами, навыки решения простейших уравнений;
• развивать быструю работу мысли и внимательность.
Воспитательные:
• создать у школьников положительную мотивацию к выполнению умственных и практических действий;
• развивать интерес у учащихся не только к содержанию, но и к процессу овладения воспитать у учащихся чувство удовлетворения от возможности показать на уроке свои знания.
Развивающие:
• развитие речи;
• формирование умений сравнивать, обобщать факты и понятия;
• развитие у учащихся самостоятельности;
• развитие внимательности при поиске ошибок.
Оборудование:
• мультимедийный проектор;
• карточки.
Ход урока:
Организационный момент.
Актулизация опорных знаний
А3. Найдите значение выражения:

А4. Преобразуйте в многочлен стандартного вида:

Повторение пройденного материала:
Для разложения на множители суммы кубов используется тождество
 (1)
(1)
Которое называют формулой суммы кубов.
Чтобы доказать тождество (1), умножим двучлен a+b на трехчлен 

Множитель  в правой части формулы (1) напоминает трехчлен
в правой части формулы (1) напоминает трехчлен  который равен квадрату разности a и b. Однако вместо удвоенного произведения a и b в нем стоит просто их произведение. Трехчлен
который равен квадрату разности a и b. Однако вместо удвоенного произведения a и b в нем стоит просто их произведение. Трехчлен 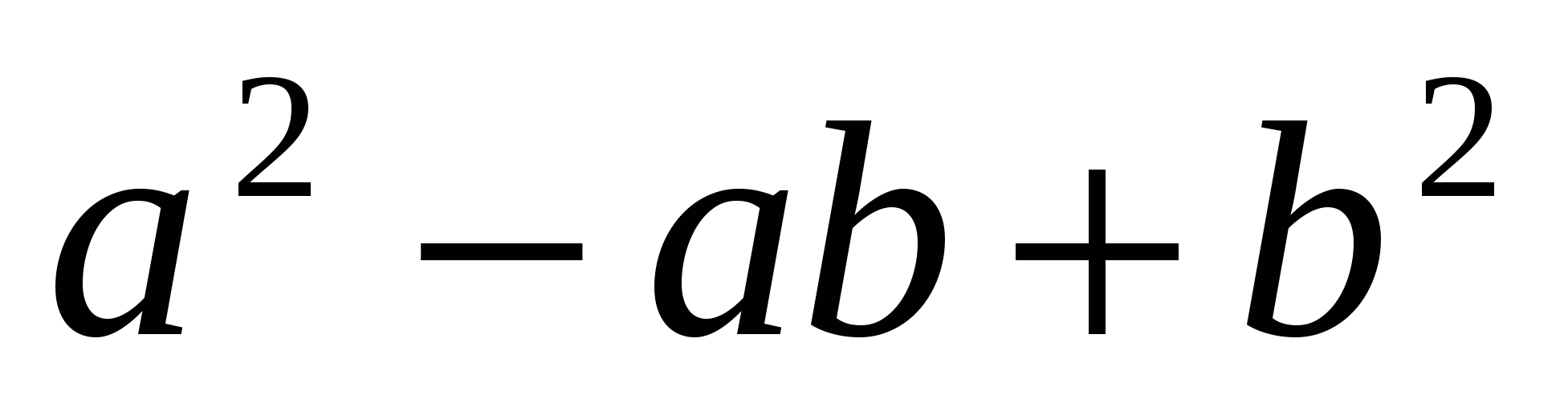 называют неполным квадратом разности a и b. Итак,
называют неполным квадратом разности a и b. Итак,
сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
Пример 1. Разложим на множители многочлен  .
.
Данный многочлен можно представить в виде суммы кубов двух выражений:


Применив формулу (1), получим

Итак,

Для разложения на множители разности кубов используется тождество
 (2)
(2)
Которое называют формулой разности кубов.
Чтобы доказать тождество (2), преобразуем произведение двучлена a-b и трехчлена  , который называют неполным квадратом суммы a и b:
, который называют неполным квадратом суммы a и b:
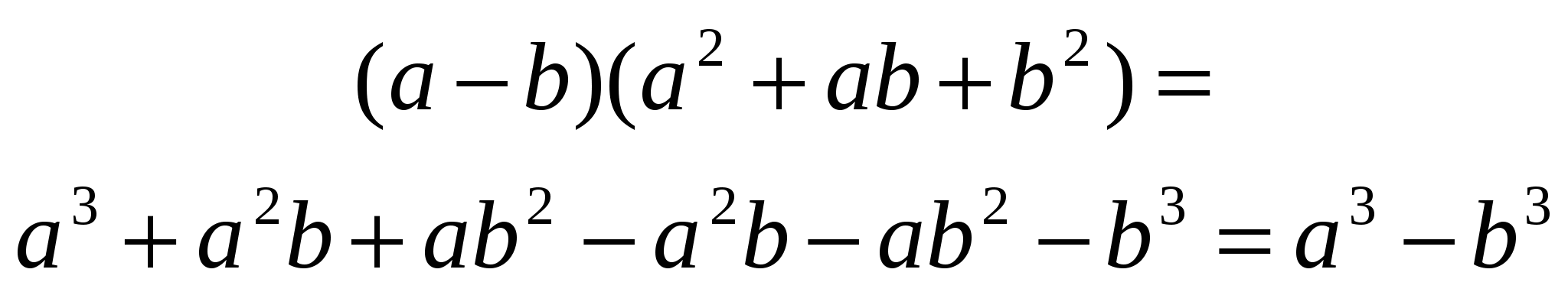
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Пример 2. Разложим на множители  .
.
Представим данный многочлен в виде разности кубов двух выражений и применим формулу (2). Получим

Закрепление нового материала: № 905, № 907, № 912.
№ 905. Разложите на множители многочлен:
а) 
б)
в) 
г) 
д) 
е) 
№907. Представьте выражение в виде суммы или разности кубов и разложите его на множители:
а) 
б)
в)
г)
д)
е)
№ 912. Представьте в виде произведения:
а)
б)
в)
г)
д)
е)
V. Домашнее задание: №865
VI. Итог урока:
• проанализировали контрольную работу;
• разобрали задачи вызвавшие затруднения при решении;
• познакомились с новыми формулами, неполным квадратом разности и суммы.
















