Урок математики, 9 класс Учитель Бродяная Наталья Леонидовна
Дата 08.12.2019
Урок по теме «Решение неравенств второй степени с одной переменной».
Цель урока : обучение решению неравенства второй степени с одной переменной на основе свойств квадратичной функции
За дачи: создать условия на уроке для выработки алгоритма решения неравенств на основе свойств квадратичной функции, формировать умения решать неравенства данного вида.
способствовать активизации познавательной деятельности учащихся, формированию навыков самопознания, аргументированной речи, умений делать обобщения на основе данных, полученных в результате исследований, развитию графической и функциональной культуры учащихся.
содействовать воспитанию у учащихся стремления к самосовершенствованию, коммуникативных качеств, повышению интереса к изучению математики,
формированию навыков общения, умения работать индивидуально и в группах.
Специальная задача:
Совершенствование навыков ориентировки на координатной плоскости, смена видов деятельности. Развитие памяти, объёма внимания. Тренировка аккомодационной мышцы.
Тип урока: урок открытия новых знаний.
Методы обучения: объяснительно-иллюстративный, вопросно-ответный, наглядный, словесный (рассказ, беседа, диалог), поисковый с элементами исследования, эвристический методы, дифференцированный подход.
Формы организации деятельности учащихся : коллективная форма работы (фронтальный опрос, устная работа), индивидуальная работа (по карточке), письменная работа.
Оборудование:
Раздаточные материалы:
карточки для индивидуальной работы, алгоритм «Решение неравенств второй степени с одной переменной»
Ход урока
Организационный момент. Мотивация учащихся к активной учебно- познавательной деятельности на основном этапе урока (1- 2 мин)
(Дети настраиваются на урок).
Здравствуйте, ребята. Сегодня у нас необычный урок, присутствуют гости.
«С тех пор как существует мирозданье, Такого нет, кто б не нуждался в знанье. Какой мы ни возьмем язык и век,
Всегда стремится к знанью человек»
Я вам желаю прочных знаний по теме урока,
творческих успехов в рамках предстоящей математической недели.
Сообщение темы, основной цели урока. Проблемные вопросы (8 мин) (Включение детей в учебную деятельность)
Цель: развитие познавательных интересов учащихся.
Сегодня вам предстоит продолжать самостоятельно открывать новые знания по теме, которую мы начали изучать на прошлом уроке. Как вы думаете, что мы будем исследовать? Назовите эту тему. («Решение неравенств второй
степени с одной переменной»).
Продолжим работу над ней.
Итак, тема нашего урока «Решение неравенств второй степени с одной переменной».
Откроем тетради. Запишем дату и тему урока. (Записать её на доске).
Мотивация. Почему такое внимание уделяем неравенствам второй степени? (Дети отвечают на вопрос)
Потому что это одна из самых важных тем курса алгебры.
Более сложные, пока еще незнакомые для вас неравенства вы будете решать в старших классах, и почти все они будут приводиться к решению неравенств второй степени. Особое внимание неравенствам уделяется еще и на ГИА и ЕГЭ, на вступительных экзаменах. Поэтому уже сейчас вы должны иметь четкие представления о решении неравенств второй степени.
Что нам удалось установить на прошлом уроке? (Графическую связь между неравенством и соответственной квадратичной функцией).
- А как мы уже можем решать неравенства второй степени с одной переменной? (Неравенства учились решать с помощью параболы, то есть графическим способом посредством свойств квадратичной функции).
- Что будет в решении центром нашего внимания? (Парабола)
- С какой точностью построенная и какие расположения ее могут быть на координатной плоскости? Неужели придется строить параболу по алгоритму?
- А что для этого нам осталось выработать, создать? С помощью чего нам легче было разбираться со сложной квадратичной функцией? ( С помощью алгоритма – схемы решения).
- Кто сможет сформулировать основную цель урока? (Дети обосновывают цель урока).
Основная образовательная цель: формировать умения решать неравенства второй степени с одной переменной на основе свойств квадратичной функции с помощью алгоритма.
Где находят применение эти неравенства? (В окружающем нас мире)
Итак, восхитимся своими знаниями архитектуры, строительства. И с целью снятия мышечного напряжения, сменим позу и вид деятельности. Подойдем к телевизору на удобное для каждого из вас расстояние. Посмотрите на экран.







Физминутка для глаз для снятия напряжения глаз. Пальминг.
Назовите некоторые свойства квадратичной функции, которые здесь использовались? (Область определения и область значения функции; промежутки убывания, возрастания функции; наибольшее и наименьшее значения).
Какое свойство квадратичной функции будем использовать мы при графическом способе решения неравенств второй степени с одной переменной? (Отыскание промежутков, в которых квадратичная функция сохраняет знак, то есть промежутков знакопостоянства функции).
Так как можно рассматривать решение неравенства второй степени с одной переменной? (Нахождение промежутков, в которых квадратичная функция принимает положительные или отрицательные значения).
Что для этого достаточно исследовать, проанализировать? (Как расположен график квадратичной функции в координатной плоскости).
И как же он может быть расположен? От чего это зависит? (От а и Д).
Какие неравенства называются неравенством второй степени с одной переменной? (Неравенства вида ax2 + bx + c 0 и ax2 + bx + c 0, где x- переменная, a, b и c - некоторые числа и a≠ 0, называют неравенствами второй степени с одной переменной).
- Как можно назвать такие неравенства? (Строгие неравенства).
- Почему?
А еще какие бывают? (Нестрогие неравенства, если квадратный трехчлен будет сравниваться с 0 знаком 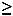 или ≤).
или ≤). Сколько решений может быть? Всегда ли явным будет ответ, посмотрев лишь на неравенство? (Дети высказывают свои предположения, идеи, гипотезы: нет, его надо прежде решить).
Цель поставлена, начнем действовать. С чего начнем? Выстроим план работы.
Повторение изученного Проверка домашнего задания
Составление алгоритма решения неравенств второй степени, основанный на свойствах квадратичной функции
Применение его к решению неравенств второй степени
Переходим к следующему этапу.
Ш. Актуализация опорных знаний и умений учащихся. Проверка домашнего задания (8 мин)
Цель:
повторение тех знаний, которые необходимы для открытия нового знания.
Фронтальный опрос.
Итак, сегодня нам предстоит открыть новые знания. Прежде чем совершать открытие, давайте проверим себя, готовы ли мы совершить его, всё ли было усвоено на уроках. Для этого проведём разминку по изученному материалу.
Сначала повторим необходимые для нас сведения о квадратичной функции. Назовите её формулу (y = ax2 + bx + c, где a≠0).
ветви параболы направлены вверх,
ветви параболы направлены вниз,
если дискриминант больше нуля, то парабола пересекает ось абсцисс в двух точках,
если дискриминант равен нулю, то парабола касается оси абсцисс,
если дискриминант меньше нуля, то парабола не пересекает ось абсцисс,
абсцисса вершины параболы равна … 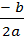 .
.
Самостоятельная работа (подготовительные задания, аналогичные домашним).

(Дети выполняют
по карточкам на местах в два варианта )
Специальные приёмы:
Работа с тифлоприборами (лупами), текст увеличен, шрифт 18.
Самостоятельная работа
Назовите решения неравенств ax2 + bx + c 0 и ax2 + bx + c , если график соответствующей квадратичной функции расположен следующим образом:
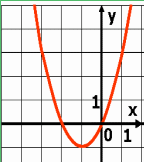
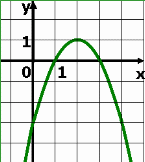
- Покажите штриховкой соответствующие промежутки на каждом рисунке разными цветами.
Цель: координирование слаженной работы.
- Как нашли указанные промежутки? Проверим себя.
Учащиеся записывают ответы на карточке под соответствующим рисунком. Подходят к доске, сверяют их с верными ответами, записанными заранее учителем на маркерной доске под рисунками с обратной стороны:
Первый рисунок - I вариант
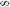
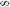 ax2 + bx + c 0 на (- ; - 2)U (0;+ );
ax2 + bx + c 0 на (- ; - 2)U (0;+ );
ax2 + bx + c 0 на (-2;0). Второй рисунок - II вариант ax2 + bx + c 0 на (1;3).
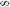
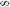 ax2 + bx + c 0 на (- ; 1) U (3;+ ).
ax2 + bx + c 0 на (- ; 1) U (3;+ ).
(Выслушиваются варианты ответов детей).
Обоснуйте свои решения. (Дети комментируют решение по одному от варианта у доски, показывая штриховкой соответствующие интервалы на каждом рисунке разными цветными маркерами).
Специальные приёмы Цветовая унификация
Сделаем вывод. Что мы отыскали? (Решения неравенства второй степени с одной переменной, соответствующего квадратичной функции, заданной параболой).
IV. Формирование новых понятий (8 мин)
Кто может сформулировать алгоритм решения неравенств второй степени, основанный на свойствах квадратичной функции.
Физминутка. Для снятия напряжения выполним комплекс физических упражнений, посвященных параболе (Звучит музыка)
Мы старались, мы учились И немного утомились, Сделать мы теперь должны. Упражнения для спины.
Первое упражнение. И.П.Руки, согнутые в локтях параболой, - на пояс, Наклоны (вправо, влево, вперед, назад).
Начали наклоны:
/ 2- направо, 2 – налево, 2 – вперед, 2 – назад/
Второе упражнение. И.П. Руки в замок за спиной.
Затем по очереди положить руки на противоположное плечо: Правая - сверху, левая – снизу
Потом наоборот (поменять положение рук), так несколько раз. Упражнение для ног.
Чтобы ноги не болели, раз присели (встали), два присели (встали), Три, четыре, пять и шесть.
А теперь всем тихо сесть. Упражнения для снятия напряжения
Наклоны головы:
/ направо - прямо, налево - прямо, вперед - прямо, назад - прямо/ (Повторить два раза).
Проблемный диалог с учащимися
Выбрать из перечисленных:
знак D квадратного трёхчлена;
направление ветвей параболы;
пересечение параболы с осями координат;
координаты вершины параболы;
примерное расположение параболы?
Алгоритм решения неравенств второй степени, основанный на свойствах квадратичной функции (раздать карточки учащимся)
Рассмотрите функцию
y=ax2+bx+c
Определите направление ветвей
Найдите точки пересечения параболы с осью абсцисс (для них y=0; х1и х2 найдите, решая уравнение ax2+bx+c=0)
Схематически постройте график функции y=ax2+bx+c
Выделите часть параболы, для которой y0 (y
По схематическому изображению параболы записать множество решений неравенства.
Объясните, с чего начнете решение неравенств второй степени? Цель: проверить качество запоминания нового материала Дети отвечают устно по очереди, не глядя в текст.
Графический способ решения квадратного неравенства
Задать функцию
Определить направление ветвей параболы по знаку коэффициента а; з. Найти корни соответствующего квадратного уравнения
или установить, что их нет;
Построить эскиз графика квадратичной функции;
По графику определить промежутки, на которых функция принимает нужные значения.
Записать ответ.
Закрепление изучённого материала. Решение квадратных неравенств.
(7 мин)
Цель: первичное закрепление нового материала
- Решать такие неравенства мы будем с помощью нахождения промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.
Итак, выполним в тетрадях следующее задание:
Решить неравенство: 5х2 + 9х – 2 0.
Оформление в тетрадях. 5х2+9х-2
Рассмотрим функцию y=5х2+9х-2
Графиком функции является парабола, ветви которой направлены вверх.
Найдем нули функции, у = 0. 5х2+9х-2=0
D = 81 + 40 = 121,
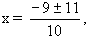
х1= -2; х2= 0,2
Схематически построим график функции
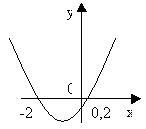
Из рисунка видно, что функция принимает орицательные значения при
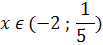
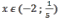 Ответ:
Ответ:
Рассмотрим пример 2 в учебнике на странице 84 самостоятельно. Сделаем соответствующие выводы в общем виде. (Укрупненный текст на А - 4).
Применение знаний, формирование умений и навыков. Обучающая самостоятельная работа. Работа в парах. ( 5 мин)
Цель: проверить качество усвоения нового материала
1.Решить неравенство: 5х2 + 9х – 2 0.
Решение разобрать прежде устно. Чем отличается от примера 1? в чем сходство с примером 2? Сопоставляйте шаги с алгоритмом.
Какая квадратичная функция соответствует данному неравенству: 1. у = 5х2 + 9х – 2
Что является её графиком? 2.
Как направлены ветви параболы ? 3.
Как расположена парабола относительно оси х? Как она может быть расположена (пересекать ось х, находиться выше оси х, ниже оси х, касаться
оси х)?
Как это определить? Нули функции, у = 0. 5х2 + 9х – 2 = 0,
D = 81 + 40 = 121,
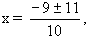
х1 = 0,2 , х2 = -2.
Покажем схематически, как расположена парабола в координатной плоскости.
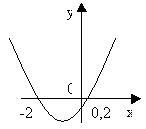
Из рисунка видно, что функция принимает положительные значения при
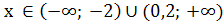 .
.
Ответ: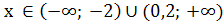 .
.
Дети после разбора самостоятельно решают неравенство. Учитель оказывает помощь детям, испытывающим затруднения
Чему учились? Что важное для себя открыли?
Домашнее задание. (1- 2мин)
п.14, разобрать примеры 1, 2, стр.83 - 84
№304 (а, б)
В дополнительной литературе или с помощью Интернет-ресурсов постарайтесь найти нерассмотренные на уроках области применения квадратных неравенств.
.Подведение итогов урока: (2 мин)
Учитель просит учащихся оценить, как они справились с работой на уроке, что было удачным, и в чем наблюдалась сложность при решении задач; на какие, по их мнению, вопросы следует обратить внимание на следующем уроке.
Достигнута ли цель каждым?
Ребята, большое спасибо за урок. Я бы хотела увидеть, какое у вас настроение. Я предлагаю вам выбрать на стенде смайлик по своему настроению.
. Дополнительные сведения для учащихся (на память). Интересные свойства параболы:
1. Любая точка параболы равноудалена от некоторой точки, называемой фокусом параболы, и некоторой прямой, называемой ее директрисой.
2. Если вращать параболу вокруг оси симметрии (например, параболу y = x2 вокруг оси Oy), то получится очень интересная поверхность, которая называется параболоидом вращения.
Поверхность жидкости во вращающемся сосуде имеет форму параболоида вращения. Вы можете увидеть эту поверхность, если сильно помешаете ложечкой в неполном стакане чая, а потом вынете ложечку.
3. Если в пустоте бросить камень под некоторым углом к горизонту, то он полетит по параболе. Если пересечь поверхность конуса плоскостью, параллельной какой-либо одной его образующей, то в сечении получится парабола
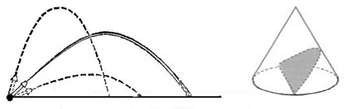
5. В парках развлечений иногда устраивают забавный аттракцион
«Параболоид чудес». Каждому, из стоящих внутри вращающегося параболоида, кажется, что он стоит на полу, а остальные люди каким-то чудом держаться на стенках.
6. В зеркальных телескопах также применяют параболические зеркала: свет далекой звезды, идущий параллельным пучком, упав на зеркало телескопа, собирается в фокус.
7. У прожекторов зеркало обычно делается в форме параболоида. Если поместить источник света в фокусе параболоида, то лучи, отразившись от параболического зеркала, образуют параллельный пучок.














 (Дети выполняют по карточкам на местах в два варианта )
(Дети выполняют по карточкам на местах в два варианта ) 

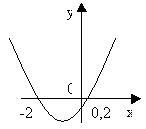
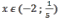 Ответ:
Ответ:










