Сборник задач "Мир графов"

Муниципальное казенное общеобразовательное учреждение

«Средняя общеобразовательная школа № 11 г.

Сборник задач по теме «Графы»

Составители: ученица 7 класса

Петрова Яна,

учитель математики

Кузьменко А.А.

г. Нижнеудинск, 2024 г.

Оглавление

Задачи………………………………………….2-8

Ответы……………………………………….9-13

Интернет-ресурсы…………………………….14

Задача№1

В нашем классе 5 человек изучает немецкий язык, остальные- английский. На уроке учитель опрашивает каждый урок одновременно 2 учеников (вопрос- ответ). Сколько пар можно составить, чтобы ученики в паре не повторялись?

Задача №2

4 человека из нашего класса захотели поздравить друг друга с 8 марта. Сделать это решили с помощью SMS-ок. Сколько всего SMS-ок было отправлено?

Задача №3

В нашем классе Александра, Никита и Валерия по медицинским показаниям могут занимать только средний ряд, 1-ю,2-ю или 3-ю парту. Чтобы помочь учителю решить спор, как рассадить учеников. Сколькими способами они могут занять имеющиеся места?

Задача №4

В нашем школе пять человек из 7 А и 7 Б классов по итогам школьной олимпиады стали призерами (Юля, Саша, Катя, Алексей, Влад). Для участия в муниципальной олимпиаде нужно было выбрать 2 человек из 5. Решили выбрать Одного из 7 А и один из 7 Б. Сколькими способами это можно сделать?

Задача №5

К учебному году мне купили школьную форму: брюки, юбка, 3 блузки (белая, голубая, розовая), две пары туфлей, жилетка. Сколько дней я могу комбинировать обувь и одежду, чтобы не повторить набор. Жилетка обязательна всегда.

Задача №6

В государстве 100 городов, и из каждого из них выходит 4 дороги. Сколько всего дорог в государстве?

Задача № 7

Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля – Меркурий, Плутон – Венера, Земля – Плутон, Плутон – Меркурий, Меркурий – Венера, Уран – Нептун, Нептун – Сатурн, Сатурн – Юпитер, Юпитер – Марс и Марс – Уран. Можно ли добраться (возможны пересадки) с Земли до Марса?

Задача № 8

Клоуны Бам, Бим, Бом вышли на арену в красной, синей и зеленой рубашках. Их туфли тоже были этих трех цветов. Туфли и рубашка Бима были одного цвета. на Боме не было ничего

красного. Туфли Бама были синие, а рубашка нет. Какого цвета были туфли и рубашка у Бома и Бима?

Задача № 9 

Оля, Дмитрий, Коля и Саша заняли первые четыре места на олимпиаде. Оля не заняла ни первое, ни последнее место, Дмитрий занял второе место, Коля оказался в числе первых трех призеров. Какое место на олимпиаде занял Саша?

Задача №10

Три ученицы – Валя, Галя и Катя – пришли в театр в платьях разного цвета: одна – в белом, другая – в сером, а третья – в черном. Катя была не в черном, Валя не в черном и не в сером. Угадай, в какое платье каждая из них была одета.

Задача №11

В классе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга (в этом классе), 11 – по 4 друга, а 10 – по 5 друзей?

Задача №12

Встретились три друга - Белов, Серов и Чернов. Чернов сказал другу, одетому в серый костюм: «Интересно, что на одном из нас белый костюм, на другом - серый и на третьем — черный, но на каждом костюм цвета, не соответствующего фамилии». Какой цвет костюма у каждого из друзей?

Задача № 13 

В семье четверо детей. Им 5, 8, 13 и 15 лет, а зовут их Аня, Дима, Оля и Катя. Сколько лет каждому из них, если одна девочка ходит в детский сад, Аня старше, чем Дима, а сумма лет Ани и Оли делится на три?

Задача № 14

Атос, Портос, Арамис и Д’Артаньян – четыре талантливых молодых мушкетёра. Один из них лучше всех сражается на шпагах, другой не имеет

равных в рукопашном бою, третий лучше всех танцует на балах, четвертый без промаха стреляет с пистолетов. О них известно следующее: 
• Атос и Арамис наблюдали на балу за их другом – прекрасным танцором. 
• Портос и лучший стрелок вчера с восхищением следили за боем рукопашника. 
• Стрелок хочет пригласить в гости Атоса. 
• Портос был очень большой комплекции, поэтому танцы были не его стихией. 
Кто чем занимается?

Задача №15

Встретились трое друзей: Белов, Рыжов и Чернов. Брюнет сказал Белову: "Любопытно, что ни у кого из нас цвет волос не соответствует фамилии, да и ты не брюнет". Какой цвет волос у каждого из друзей?

Ответы

Задача № 1

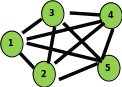(9)

Задача № 2

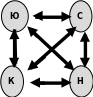(12)

Задача №3

(6)

Задача № 4

(6)

Задача № 5

(12)

Задача № 6

100·4 : 2 = 200.

Ответ.200 дорог.

Задача № 7

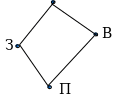
Нарисуем схему: планетами будут соответствовать точки, а соединяющим их маршрутам – непересекающиеся между собой линии.

Ме

Из рисунка видно, что земля принадлежит одной группе, а Марс – второй.

Долететь с Земли до Марса нельзя.

Задача № 8

У Бома синяя рубашка и зеленые туфли, у Бама зеленая рубашка и синие туфли.

Задача № 9

Последнее (четвертое)

Задача № 10

Валя – в белом, Галя – в черном, Катя – в сером

Задача № 11

В соответствующем графе было бы 30 вершин, 9 из которых имели бы степень 3, 11 – степень 4, 10 – степень 5. Однако у такого графа 19 нечётных вершин, что противоречит задаче. Не может.

Задача № 12

Чернов в белом костюме, Белов - в сером, Серов - в черном.

Задача № 13

Анне – 13 лет, Диме – 8 лет, Оле – 5 лет, Кате – 15 лет.

Задача № 14

Арамис – стрелок; Д’Артаньян – танцор; Портос – шпажист; Атос – рукопашник.

Задача № 15

Белов – рыжий, Чернов – блондин, Рыжов – брюнет.

Интернет-ресурсы

1. https://infourok.ru/sbornik-zadach-s-resheniyami-po-teme-grafi-3706281.html

2. http://pmk.tversu.ru/share/333.pdf

3. https://multiurok.ru/files/grafy-teoriia-i-podborka-zadach-pro-grafy.html

4. https://vk.com/wall-16108331_178398

5. https://www.eduportal44.ru/koiro/enpj/DocLib7/2020/57(2)_2020/Информатика/Макарушина%20ИА.pdf