Практическое занятие
Уравнение касательной в общем виде.
Производная: механический и геометрический смысл производной.
1) Теоретический этап
Опорный конспект.
Уравнение касательной: y = f ( ) + f '(
) + f '( ) · ( x –
) · ( x –  )
)
Алгоритм нахождения уравнения касательной:
1) Вычислить f( )
)
2) Найти производную функции f ′(x)
3) Вычислить f ′( )
)
4) Внести числа  , f(
, f( ), f ′(
), f ′( ) в уравнение касательной и упростить его.
) в уравнение касательной и упростить его.
Физический (механический) смысл производной – это скорость изменения расстояния:
s'(t) = v(t)
Геометрический смысл: f '(хо) – это коэффициент угла наклона касательной к оси Ох
f '(хо) = k = tg α
2) Подготовительный этап. Перепишите и заполните пропуски:
Пример 1. Дана функция f (x) = x3. Составить уравнение касательной к графику этой функции в точке  = 2.
= 2.
Решение: Уравнение касательной: y = f ( ) + f '(
) + f '( ) · ( x –
) · ( x –  ). Точка
). Точка  = 2 нам дана, а вот значения f (
= 2 нам дана, а вот значения f ( ) и f (
) и f ( ) придется вычислять.
) придется вычислять.
1) f ( ) = f (2) = 23 = …
) = f (2) = 23 = …
2) f (x) = (x3) = 3x2
3) f ( ) = f (2) = 3 · 22 = 3
) = f (2) = 3 · 22 = 3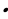 4 = …
4 = …
4) y = 8+ 12 · (x − 2) = 8 + …x − 24 = 12x − 16
y = 12x − 16
Ответ: y = 12x − 16.
Пример 2. Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке  =
= 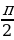 .
.
Решение: y = f ( ) + f '(
) + f '( ) · ( x –
) · ( x –  )
)
1) f ( ) = f (
) = f (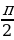 ) = 2sin (
) = 2sin (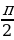 ) + 5 = 2 + 5 = …
) + 5 = 2 + 5 = …
2) f (x) = (2sin x + 5) = 2cos x
3) f ( ) = f (
) = f (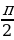 ) = 2cos (
) = 2cos (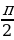 ) = 0
) = 0
4) y = 7 + 0 · (x − 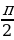 ) ; y = ...
) ; y = ...
Ответ: y = 7.
Пример 3. Составьте уравнение касательной к графику функции f(x) = 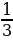 х3 – 4х + 1
х3 – 4х + 1
в точке M(3; – 2).
Решение: Точка M(3; – 2) является точкой касания, значит  = 3
= 3
y = f ( ) + f '(
) + f '( ) · ( x –
) · ( x –  )
)
1) f(3) = 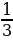 · 33 – 4 · 3 + 1 = 9 – 12 + 1 = 10 – 12 = …
· 33 – 4 · 3 + 1 = 9 – 12 + 1 = 10 – 12 = …
2) f '(x) = x2 – 4
3) f '(3) = 9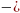 4 = …
4 = …
4) y = – 2 + 5(x – 3), y = …x – 17
Ответ: y = 5x – 17.
Пример 4. Напишите уравнения всех касательных к графику функции f(x) = x3 – 3x2 + 3, параллельных прямой f(x) = 9x + 1.
Решение: прямые параллельны, если k1 = k2.
Из формулы f(x) = 9x + 1: k1 = 9, а k2 = f '(x0)
f '(x) = 3x2 – 6x, f '(x0) = 3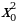 – 6x0
– 6x0
Значит, надо решить уравнение 3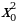 – 6
– 6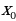 = 9; 3
= 9; 3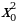 – 6
– 6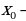 9 = 0,
9 = 0,
D = (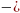 6)2
6)2 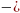 4
4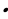 3
3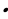 (
(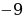 ) = 36
) = 36 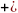 108 = …,
108 = …, 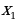 =
= 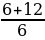 =
= 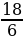 = …,
= …, 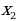 =
= 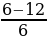 =
= 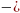
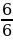 = …,
= …,
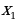 = – 1,
= – 1, 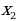 = 3
= 3
1случай: x = – 1;
1) f(x0) = f(– 1) = – 1– 3 + 3 = …
2) f '(x) = 3x2 – 6x
3) f '(x0) = f '(– 1) = 3 + 6 = …;
4) y = – 1 + 9(x + 1); y = 9x + 8 – уравнение касательной;
2случай: x = 3;
1) f(x0) = f(3) = 27–27 + 3 = …;
2) f '(x) = 3x2 – 6x
3) f '(x0) = f '(3) = 27 – 18 = …;
4) y = 3 + 9(x – 3); y = 9x – 24 – уравнение касательной.
Ответ: y = 9x + 8 и y = 9x – 24.
Пример 5. Напишите уравнение касательной к графику функции
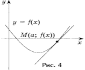 f(x) = 0,5x2 – 3x + 1, проходящей под углом 45° к прямой f(x) = 0 (рис. 4).
f(x) = 0,5x2 – 3x + 1, проходящей под углом 45° к прямой f(x) = 0 (рис. 4).
Решение: Из условия f '(a) = tg 45° = 1, f '(х) = 0,5 · 2x – 3 = x – 3
f '(a) = a – 3 ; найдем a: a – 3 = 1, a = 3 + 1 = ...
a = 4 – абсцисса точки касания, т.е. = 4.
= 4.
1) f(4) = 8 – 12 + 1 = ...
2) f '(х) = х – 3
3) f '(4) = 4 – 3 = ...
4) y = – 3 + 1(x – 4); y = x – 7 – уравнение касательной.
Ответ: y = x – 7.
3) Практический этап
Дана функция y = x3. Составить уравнение касательной к графику этой функции в точке  = 1.
= 1.
Составить уравнение касательной к графику функции f (x) = 4sin x + 5 в точке  =
= 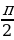 .
.
Составьте уравнение касательной к графику функции f (x) = 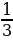 х3 – 4х + 2 в точке M(3; – 1).
х3 – 4х + 2 в точке M(3; – 1).
Напишите уравнения всех касательных к графику функции f(x) = x3 – 3x2 + 3, параллельных
прямой f(x) = 24x + 1.
Напишите уравнение касательной к графику функции f(x) = 0,5x2 – 5x + 1, проходящей под углом 45° к прямой f(x) = 0 .







 ) + f '(
) + f '( 4 = …
4 = …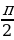 .
.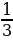 х3 – 4х + 1
х3 – 4х + 1 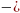 4 = …
4 = …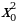 – 6x0
– 6x0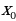 = 9; 3
= 9; 3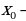 9 = 0,
9 = 0, 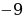 ) = 36
) = 36 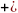 108 = …,
108 = …, 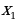 =
= 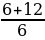 =
= 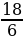 = …,
= …, 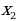 =
= 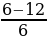 =
= 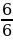 = …,
= …, f(x) = 0,5x2 – 3x + 1, проходящей под углом 45° к прямой f(x) = 0 (рис. 4).
f(x) = 0,5x2 – 3x + 1, проходящей под углом 45° к прямой f(x) = 0 (рис. 4).









