Уровневые задания "Площадь. Единицы площади"

Критерии оценки:

0 баллов – ни один ответ не является верным.

1 балл – допущена одна ошибка, остальное верно.

2 балла – верны только два ответа, остальные ошибочны.

3 балла – все ответы правильные.

Узнавание:

Задания:

1. Перед тобой три геометрические фигуры. Отметь галочкой (✓) ту фигуру, которая является квадратом.

1)

2)

3)

2. У квадрата длина стороны равна 5 см. Какова площадь этого квадрата? Обведи верный ответ.

1) 25 см²

2) 20 см²

3) 10 см²

3. Какая из предложенных формул используется для вычисления площади квадрата? Обведи правильный ответ.

1) S = a × a = а²

2) P = a + b +c +d

3) S = a × a

Цель задания: создание условий для ознакомления учащихся с основными свойствами квадрата как геометрической фигуры, формирования навыков вычисления его площади по формуле и развития умения отличать квадрат от других геометрических фигур на основе анализа их характерных признаков.

Алгоритм работы с заданием:

1.

• Прочитать задание

• Вспомнить определение квадрата

• Проанализировать каждую фигуру

• Выбрать правильный ответ

• Проверить решение

2.

• Внимательно прочитать условие задачи

• Вспомни формулу площади квадрата

• Подставить известные значения в формулу

• Сравнить полученный результат с вариантами ответов

• Выбрать и обведи правильный ответ

3.

• Внимательно прочитать вопрос

• Вспомнить определение площади квадрата

• Проанализировать варианты ответов

• Выбрать и обвести правильный ответ

Ответы детей:

1. 2)

2. 3)

3. 1)

Воспроизведение:

Задания:

1. Вставьте пропущенные слова:

Площадь – это_____ часть любой _____ геометрической фигуры.

Площадь фигуры сравнивают следующими способами:

1. _____

2. Путём _____ одной фигуры на другую.

3. Путём _____ клеток одинаковой величины.

2.

Подчеркните единицы площади:

34 см²,

26 см,

256 см,

8 см²,

12 см²,

247 м,

87 дм

3. Вставьте пропущенные значения:

В прямоугольнике ABCD поместилось 7 квадратных см. Значит, площадь прямоугольника ABCD равна ___

Цель задания: совершенствование умений определять площадь фигур, различать единицы измерения площади, применять формулы для вычисления площади и сравнивать площади различными способами.

Алгоритм работы с заданием:

1.

• прочтение предложений

• Подумать о смысле

• Вспомнить правила

• Вставить слова, чтобы предложения были логичными.

• Проверка, всё ли правильно.

2.

• Внимательно прочитать все варианты

• Анализ чисел

• Подчеркнуть правильные варианты

3.

• Внимательно прочитать условие задачи

• Вспомнить, что такое площадь

• Записать ответ

• Проверить себя

Ответы детей:

1.

Вставьте пропущенные слова:

Площадь – это__ количественная___ часть любой ___ плоской__ геометрической фигуры.

Площадь фигуры сравнивают следующими способами:

1. ___ Наложением__

2. Путём __ наложения___ одной фигуры на другую.

3. Путём подсчёта клеток одинаковой величины.

2. 34 см², 8 см², 12 см²

3. 7 см²

Понимание:

Задания:

1.

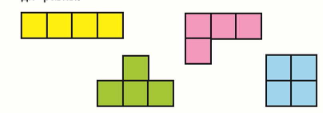
На рисунке изображены фигуры, которые при наложении не совпадут. Докажи, что их площади равны.

2.

Запиши номера фигур в порядке уменьшения их площади:

1)

2)

3)

4)

Докажи свой выбор.

3. Поставь знаки «больше»/ «меньше», докажи свой ответ:

1) 2см 20см²

2) 40дм² 4дм

3) 300 мм² 30см²

Цель задания: создание условий для применения усвоенных знаний по практическому применению знаний о площади фигур через сравнение, анализ и доказательство.

Алгоритм работы с заданием:

1.

• Прочитать задание

• Подсчет клеток

• Использование формул

• Доказательство: фигуры имеют равную площадь, потому что:

Первая фигура состоит из 8 полных клеток и 4 половинок (итого 10 клеток)

Вторая фигура - 9 полных клеток и 2 половинки (тоже 10 клеток)

Несмотря на разную форму, общая площадь одинакова

2.

• Прочитать задание

• Определение площадей фигур

• Сравнение площадей

• Обоснование выбора

3.

• Прочитать задание

• Применить изученный материал

• Доказать правильную или неправильную постановку математических знаков. перефразируй

Ответы детей:

1. все фигуры состоят из одинаковых квадратов, которые можно принять за квадратную единицу. Каждая фигура состоит из 4 квадратов, то есть площадь каждой фигуры равна 4 квадратным единицам, значит площади фигур равны.

2. 1,3,4,2

3. 1) 2 см 20см², 2) 4 дм дм², 3) 300 мм² см².

Применение в знакомых условиях:

Задания:

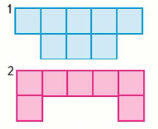
1. Сосчитай, сколько квадратных сантиметров в каждой фигуре. Сравни площади этих фигур.

2. Исправь ошибку

Дана задача

Длина прямоугольника 8 см, а ширина в 2 раза меньше. Чему равна площадь данного прямоугольника?

Коля решил таким образом

1). 8*2=16 см - ширина прямоугольника

2). 16:2=8 см2

Исправь ошибку, объясняя свои поправки.

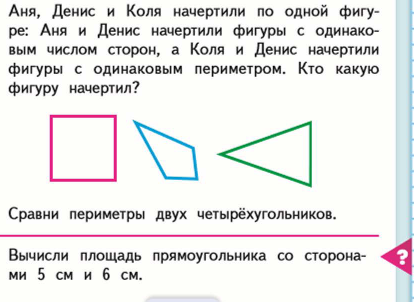
3. Аня, Денис и Коля начертили по одной фигуре: Аня и Денис начертили фигуры с одинаковым числом сторон, а Коля и Денис начертили фигуры с одинаковым периметром. Кто какую фигуру начертил? Сравни периметры двух четырехурольников.

Цель задания: Цель задания: создание условий для формирования у школьников навыков определять и сравнивать площади фигур различными способами, а также применять формулы для вычисления периметров и анализировать свойства геометрических фигур.

Алгоритм работы с заданием:

1.

• Прочитать задание

• Рассмотреть фигуры

• Определение площади каждой фигуры:

• Сравнить площади

• Записать ответ

2.

• Внимательно прочитать условие

• Выделить известные данные и что нужно найти

• Проверить каждое действие решения

• Найти ошибки и объяснить их

• Представить правильное решение

• Сформулировать ответ

3.

• Внимательно прочитать условие

• Анализ условия

• Внимательно рассмотреть рисунок

• Вспомнить, как вычислить периметр фигур

• Вспомнить, как сравнивать периметр фигур

Ответы детей:

1.

• Площадь первой фигуры — 8 см28 см2​.

• Площадь второй фигуры — 7 см27 см2​.

• Первая фигура больше второй на 1 см21 см2​.

2.

Дана задача

Длина прямоугольника 8 см, а ширина в 2 раза меньше. Чему равна площадь данного прямоугольника?

Коля решил таким образом

1). 8:2=4 см - ширина прямоугольника

2). 8*4= 32 см2

У Коли в первом действии была ошибка в том, что он увеличил длину в 2 раза, а надо было уменьшить.

Во втором действии Коля забыл, как находится площадь. Чтобы найти площадь нужно длину умножить на ширину.

3.

Ответ: Денис начертил первую фигуру, Аня вторую, Коля – третью.

8 6, значит, периметр квадрата больше периметра четырёхугольника. 

Применение в новых условиях:

Задания:

1. Длина прямоугольной клумбы 80 см, а ширина — 30 см. Вычисли площадь клумбы. Запиши решение и ответ.

2. составь алгоритм, как можно найти площадь прямоугольника, если известен периметр и одна сторона.

3. Необходимо создать проект 'Дома мечты'. Для этого постройте план дома, используя знания о том, как правильно рассчитать площадь, определить соотношение сторон и задать размеры помещений. В результате расчетов покажите площадь каждой комнаты и всего дома.

Цель задания: Оценить умение анализировать геометрические фигуры, применять формулы для вычисления площади и периметра, логически рассуждать при составлении алгоритмов, а также демонстрировать понимание пропорций и расчётов в практическом проекте.

Алгоритм работы с заданием:

1.

• Внимательно прочитать условие

• Вспомнить формулу

• Подставить значения в формулу

• Выполнить вычисления

• Записать ответ с единицами измерения

• Проверить решение

2.

• Внимательно прочитать задание

• Вспомнить изученный материал

• Записать алгоритм нахождения площади прямоугольника черз периметр и известную сторону

3.

• Прочитать задание

• Подумать над реализацией проекта

• Начертить план дома

• Вычислить площадь каждой комнаты

• Вычислить площадь всего дома

• Подготовить сообщение

• Представить свою работу в классе

Ответы детей:

1. Решение:
S = 80 см × 30 см = 2400 см²

Ответ:
Площадь клумбы составляет 2400 см22400 см2​.

2. если известны периметр и любая сторона: 1) умножьте периметр на длину известной стороны. 2) найдите квадрат известной стороны и умножьте полученное число на 2. 3) от первого произведения отнимите второе и разделите результат на 2.

3. Проект «Дом мечты»

(выполненный макет дома на бумажном носителе со схемой)

Сообщение: я представляю свой дом мечты так

(показ макета).

(Рассказ о планировке здания)