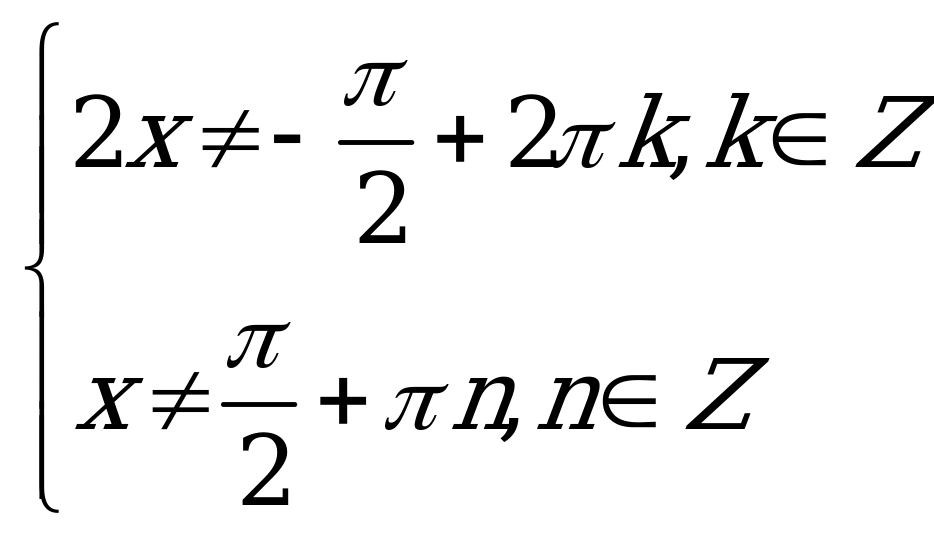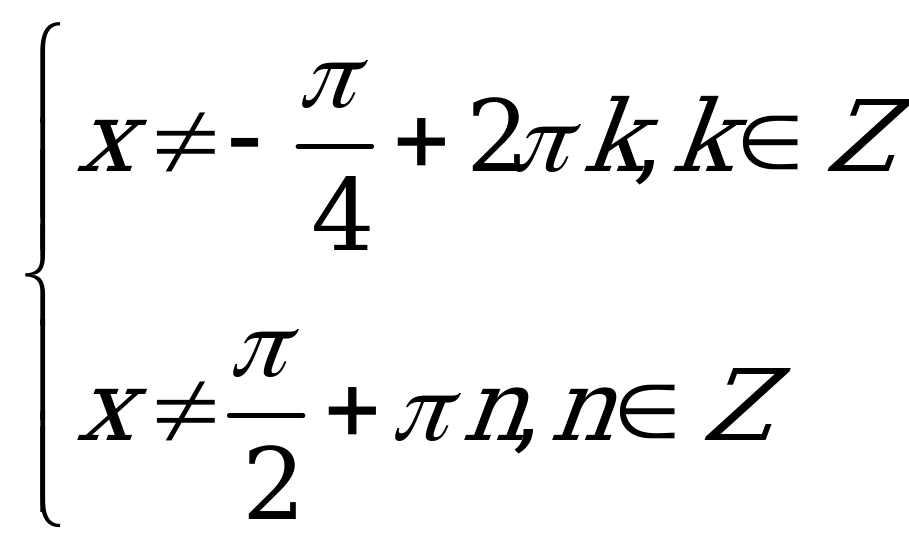С.У. Зверяка
Обособленное подразделение «МПК ЛГПУ»,
Луганск, Луганская Народная Республика
Задачи с параметрами в курсе школы
В повседневной жизни мы очень часто сталкиваемся с понятием параметра: параметр загрузки в Windows 10, параметры бытовых приборов, параметры автомобиля. Толковый словарь определяет параметр как величину, характеризующую какое-нибудь основное свойство машины, устройства, системы или явления, процесса [5].
Но в математике понятие «параметр» несколько отличается от обычного, с чем и предстоит в дальнейшем разобраться, тем более, что в школе (колледже) данная тема программой не предусмотрена.
Знакомство с математическим параметром
Основной принцип решения параметрических уравнений можно сформулировать так: необходимо разбить область изменения параметра на участки, такие, что при изменении параметра в каждом из них получающиеся уравнения можно решить одним и тем же методом. Отдельно для каждого участка находятся корни уравнения, выраженные через значения параметра, используемые для этого приемы в точности таковы, как и при решении уравнений с постоянными коэффициентами. Поскольку каждый из методов представляет собой последовательность определенных действий, которые могут выполняться по-разному в зависимости от значений параметра, то выбранные первоначально участки его изменения в процессе решения могут дробиться с тем, чтобы на каждом из них рассуждения проводились единообразно. Ответ задачи состоит из списка участков изменения параметра с указанием для каждого участка всех корней уравнения.
Пусть дано уравнение (неравенство) :

Если поставлено задание найти все такие пары 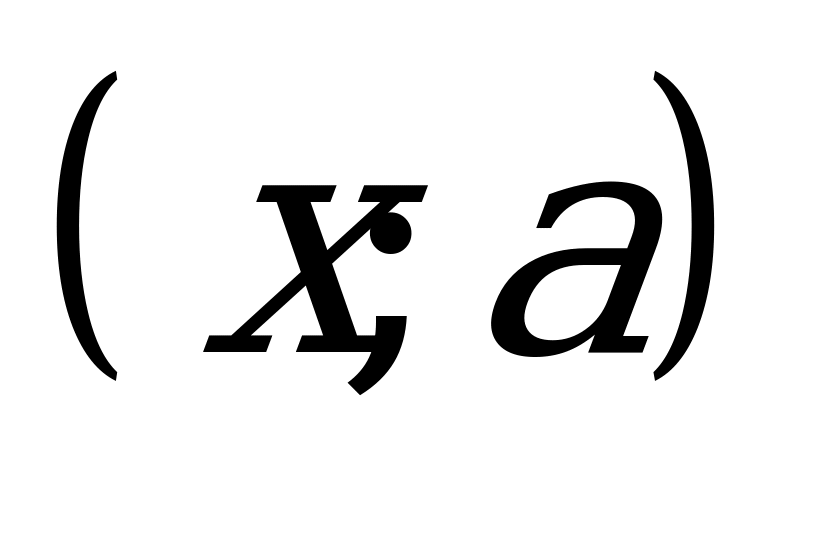 , которые отвечают требованиям данного уравнения (неравенства), то такие такие выражения будут являться уравнениями (неравенствами) с двумя параметрами x и a. Но может и другое задание – найти только x при фиксированном а. Решением таких уравнений (неравенств) будет определяться выбранными значениями а, который будет называться параметром, а множество А – областью изменения параметра.
, которые отвечают требованиям данного уравнения (неравенства), то такие такие выражения будут являться уравнениями (неравенствами) с двумя параметрами x и a. Но может и другое задание – найти только x при фиксированном а. Решением таких уравнений (неравенств) будет определяться выбранными значениями а, который будет называться параметром, а множество А – областью изменения параметра.
При этом данная область определяется множеством действительных чисел (если другого условия не поставлено), а задача решения уравнений (неравенств) с параметром заключается в нахождении семейства уравнений (неравенств) при всех действительных значениях параметра.
В работе будут рассмотрены аналитические и графические решения задач [1;3;6].
Аналитический подход
Пример 1. Решить уравнение:
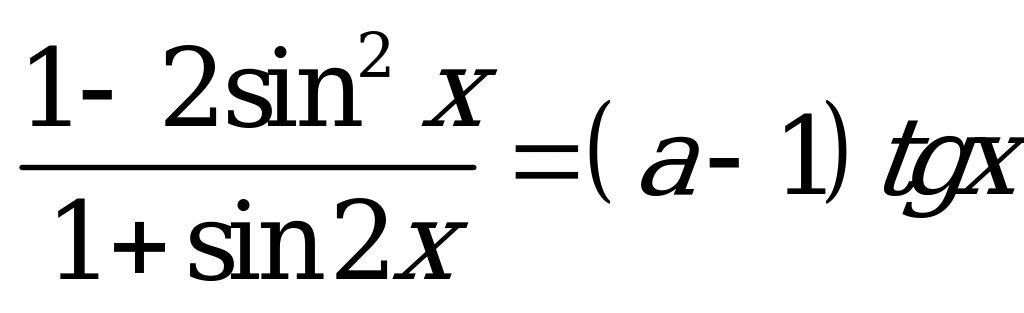
Решение:
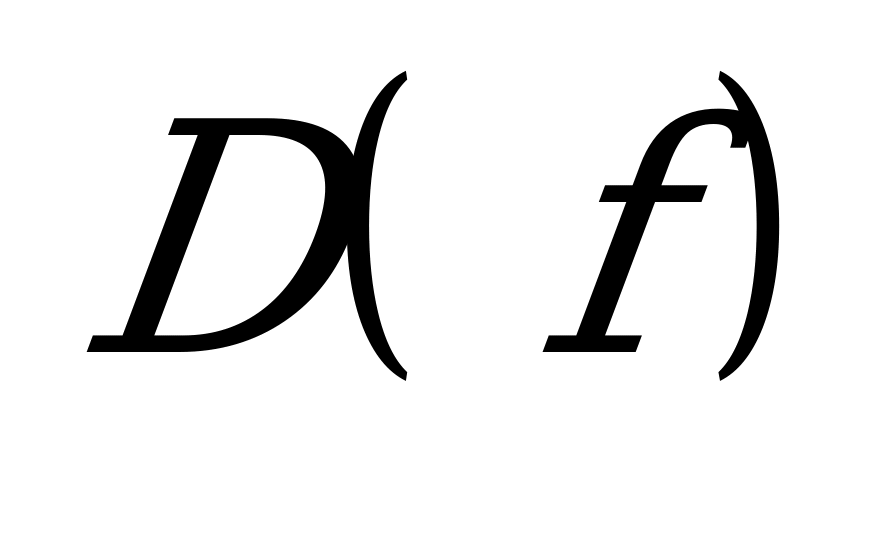 :
: 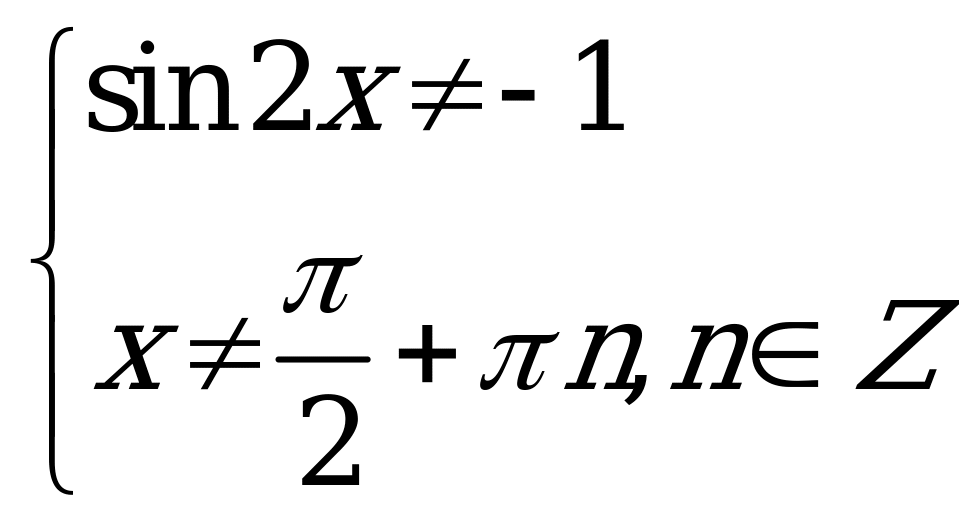 ;
; 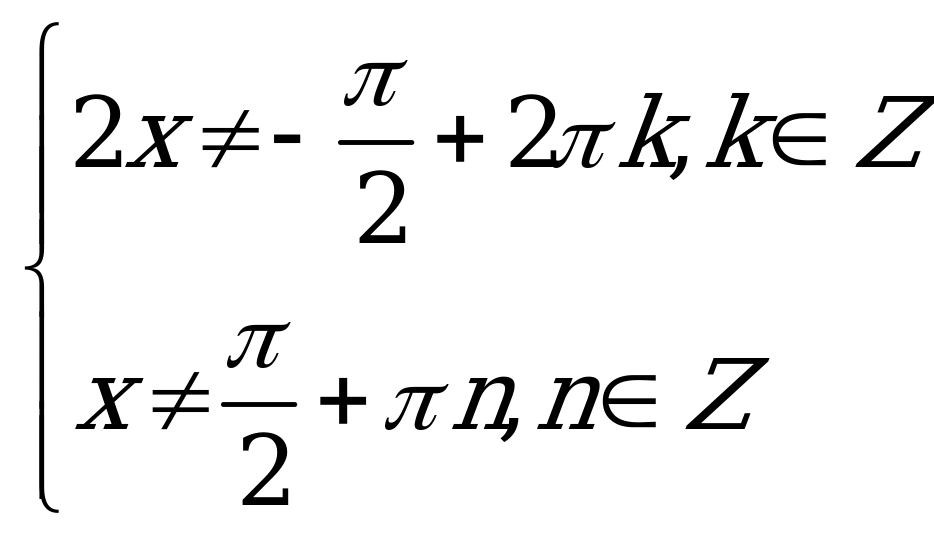
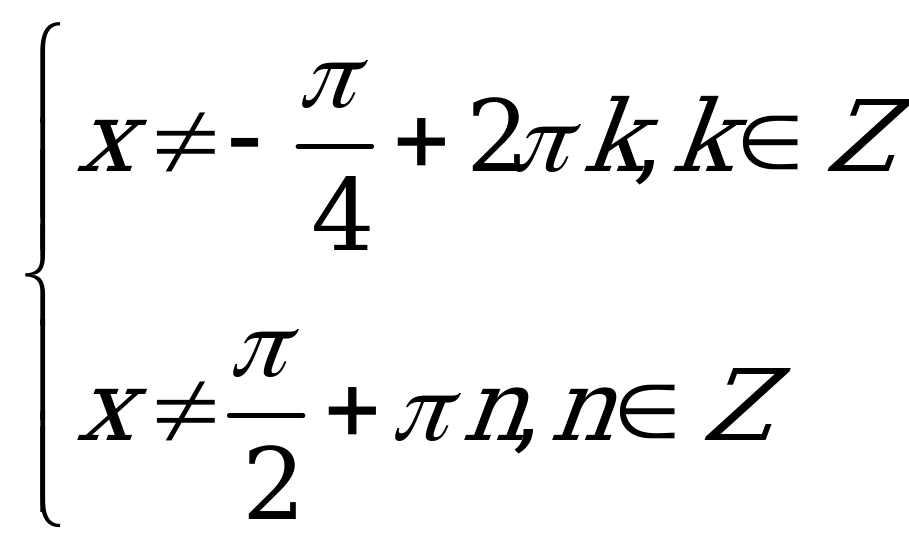
Рассмотрим следующие случаи:
1)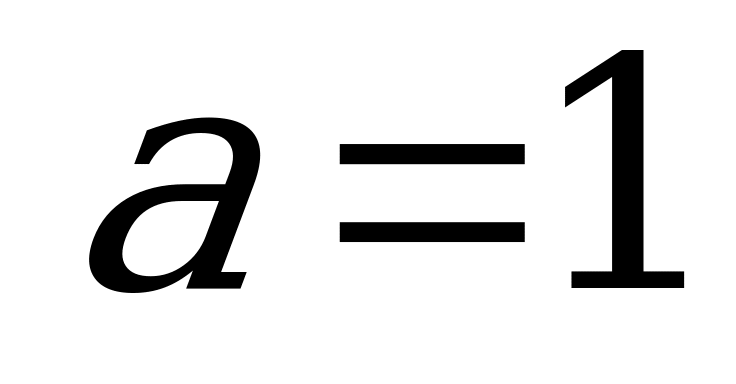 :
:
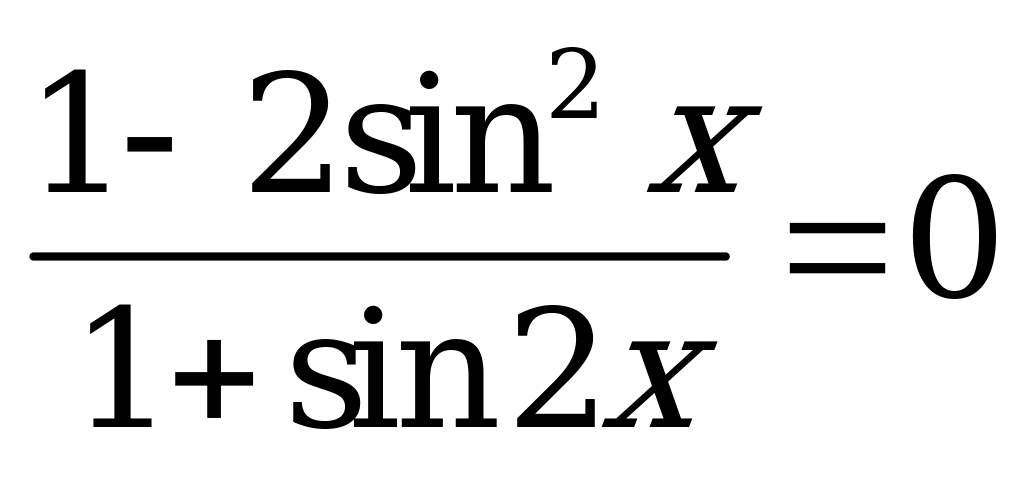 ;
; 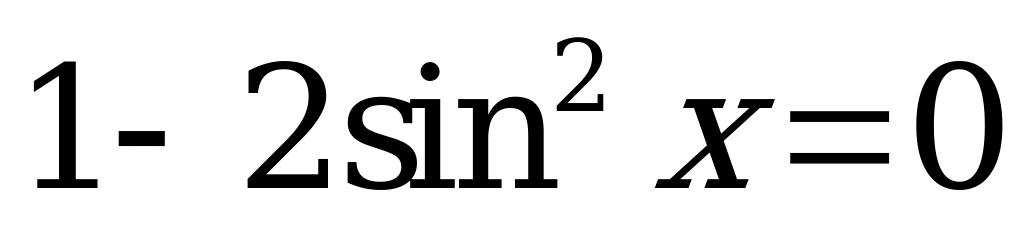 ;
;  ;
;
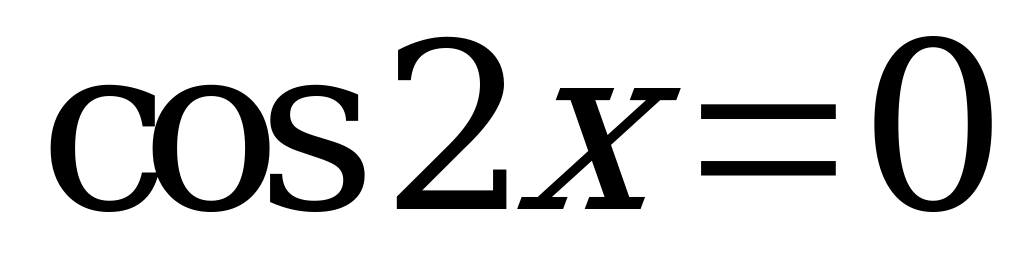
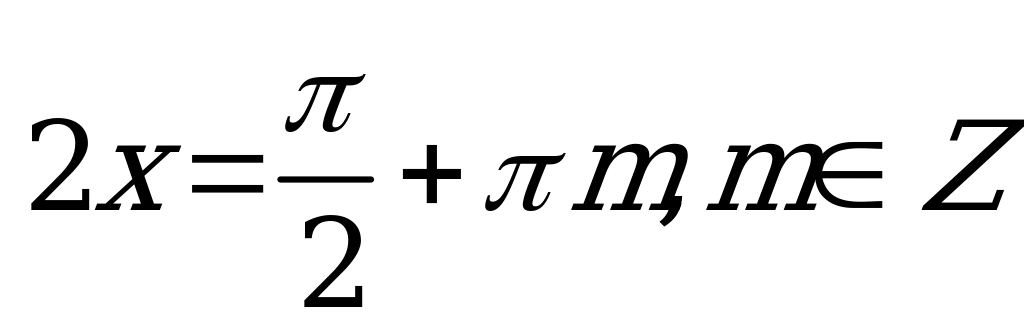 ;
; 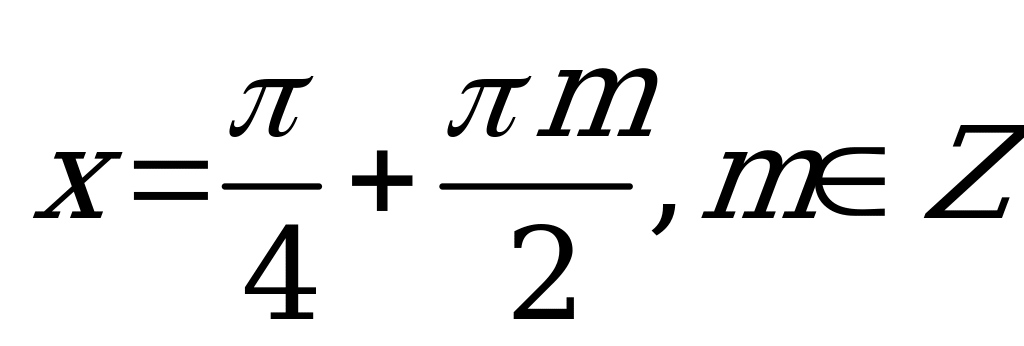
Учитывая область определения 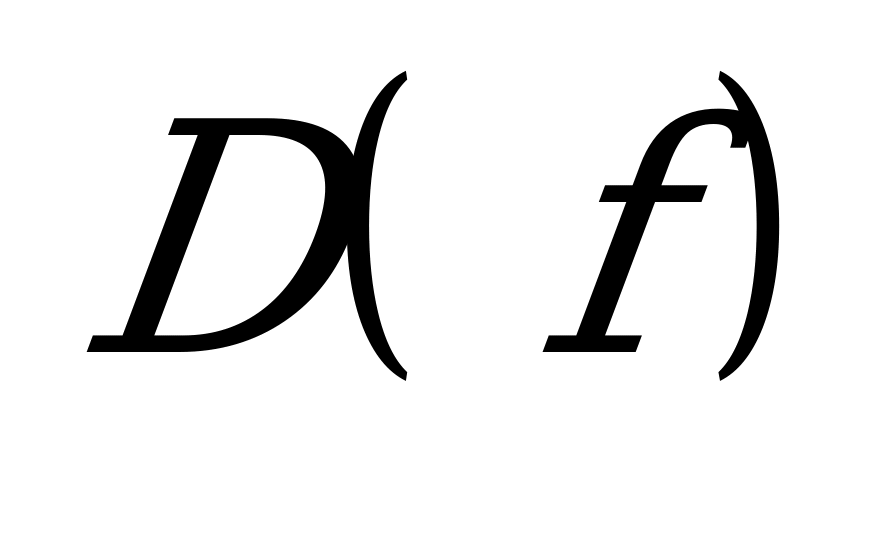 , получим окончательное решение для
, получим окончательное решение для 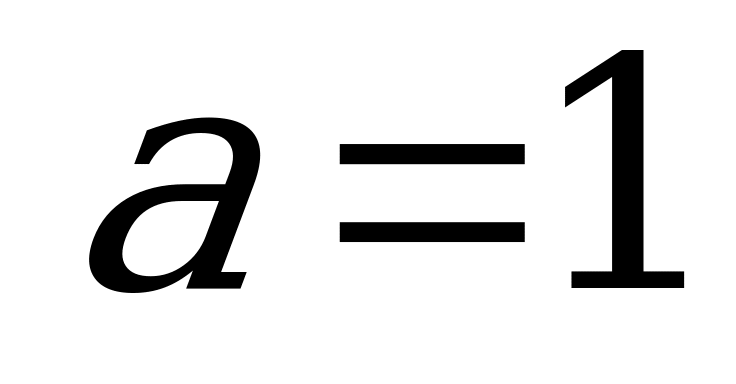 :
: 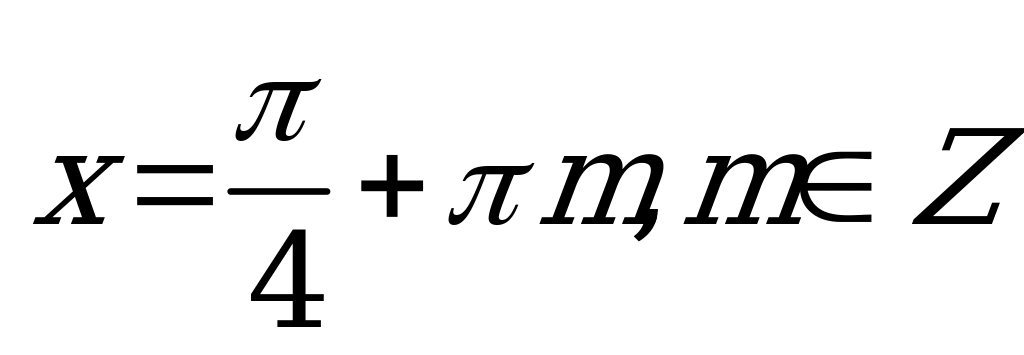 .
.
2)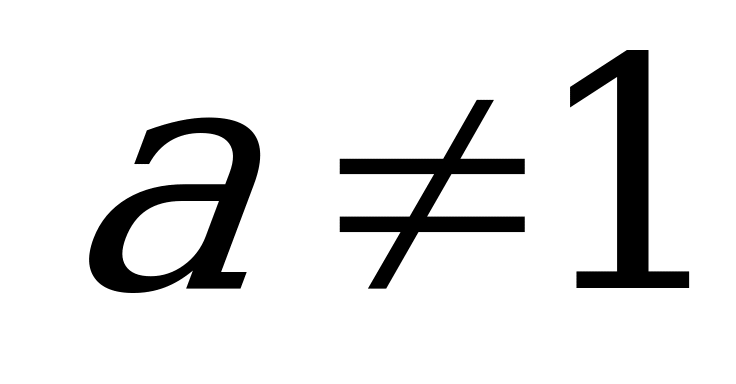 :
:
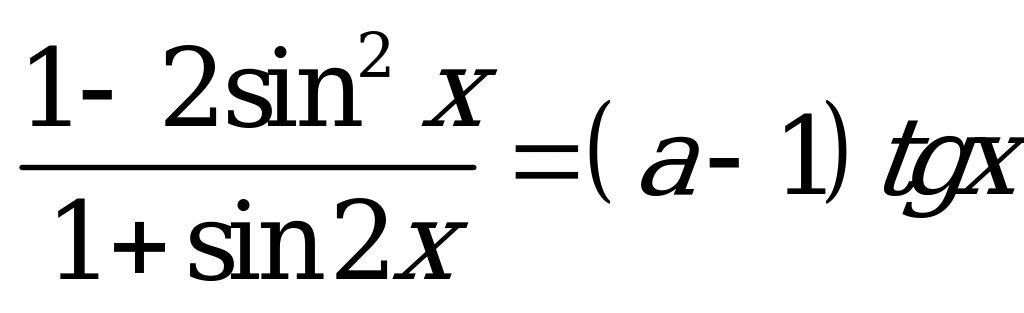
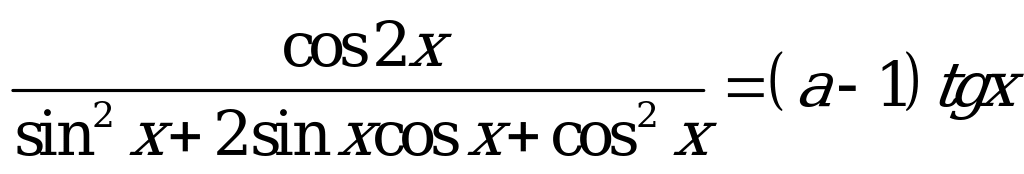
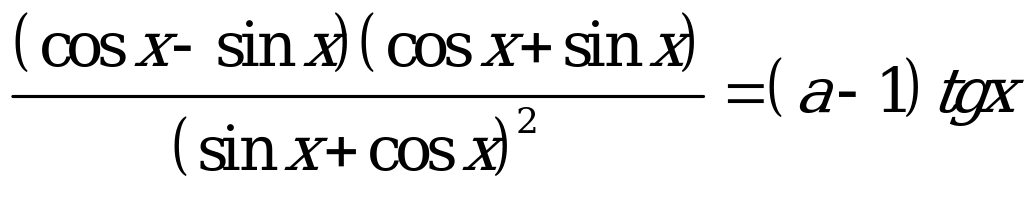
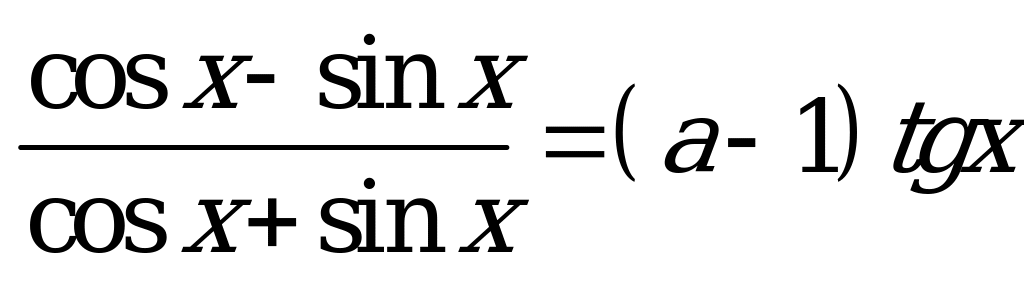
Разделим числитель и знаменатель левой части уравнения на 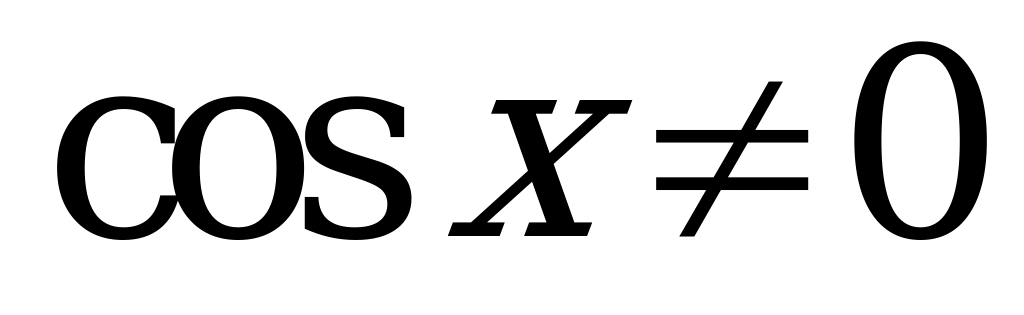 :
: 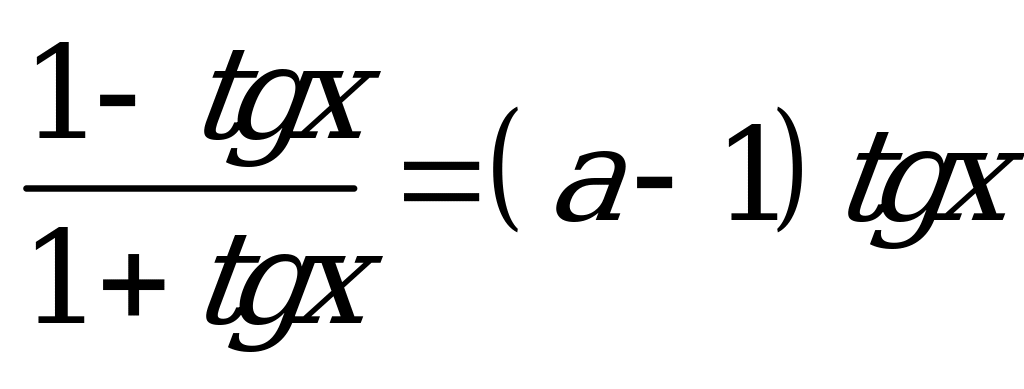
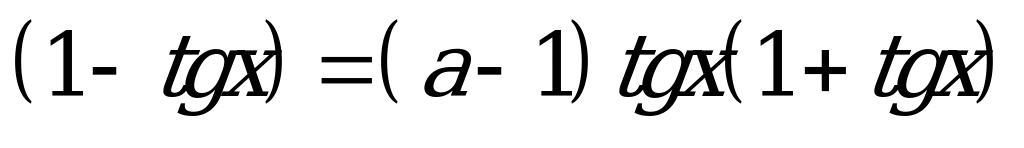
Пусть 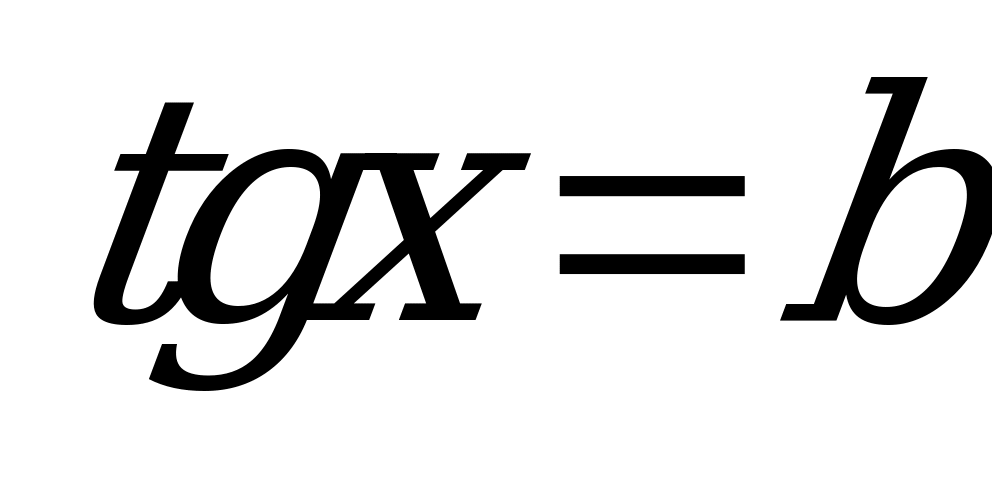 , тогда:
, тогда:
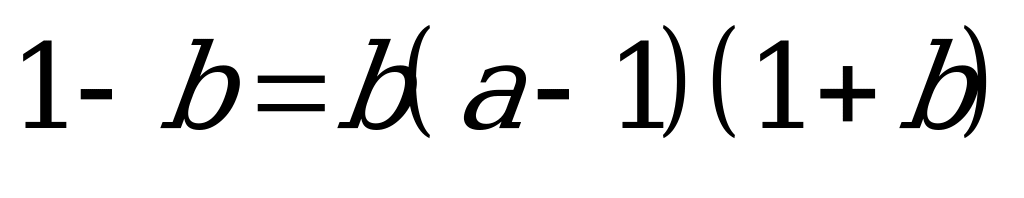 ;
; 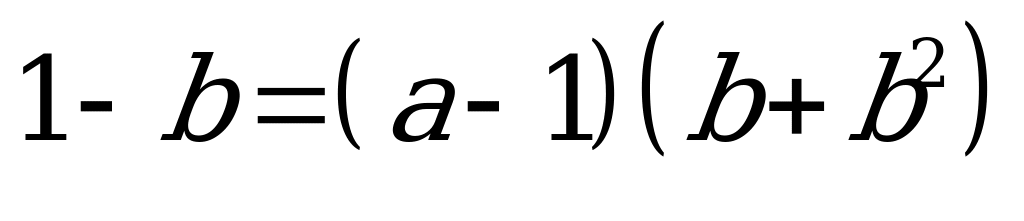 ;
;
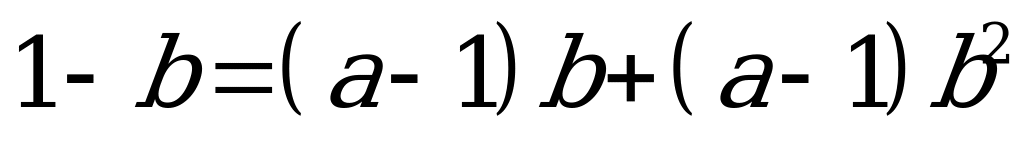 ;
; 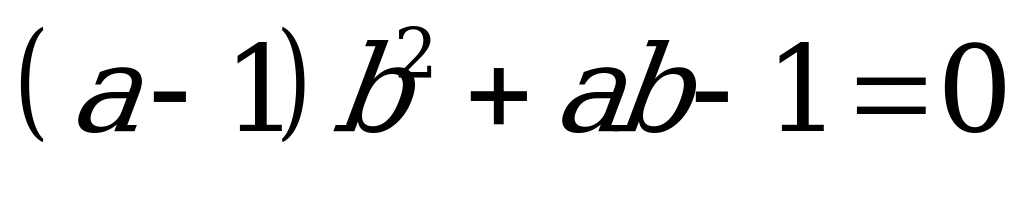
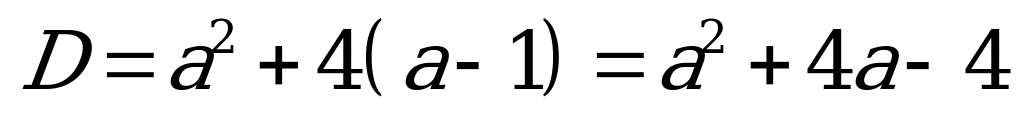
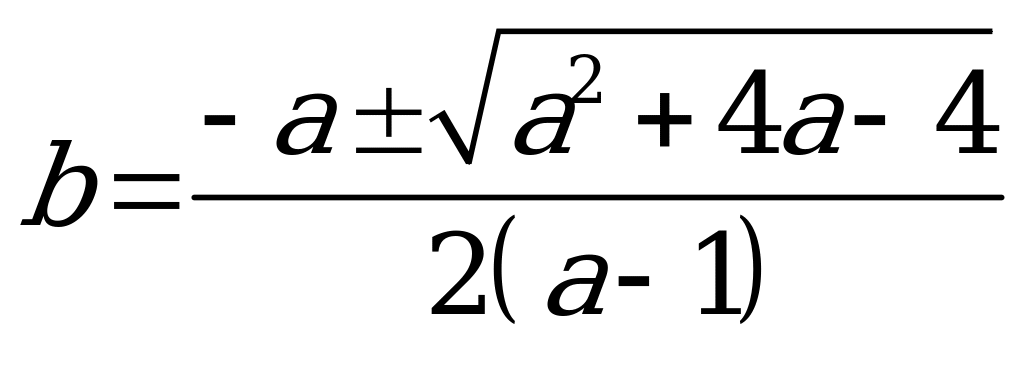
Возвращаемся к проведенной замене:
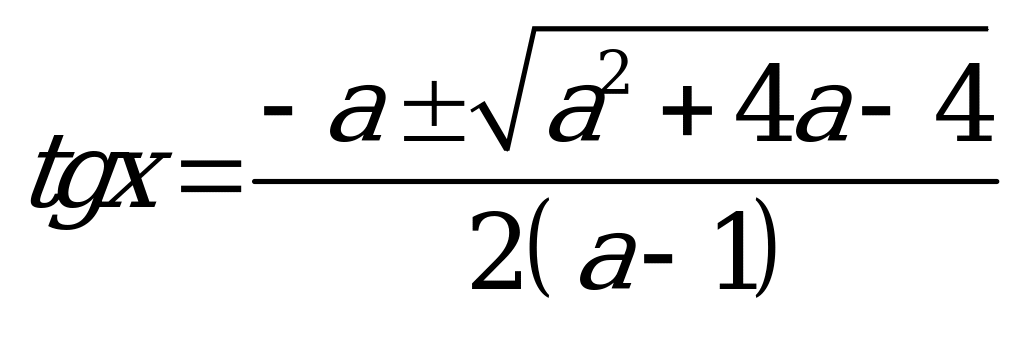
При 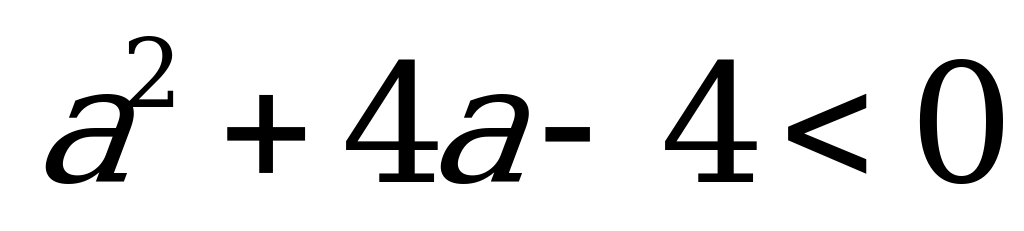 у уравнения нет решений:
у уравнения нет решений:
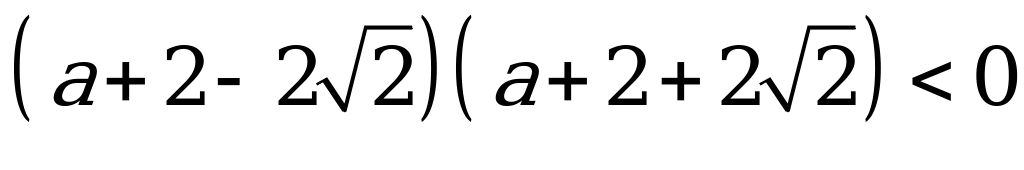 ;
; 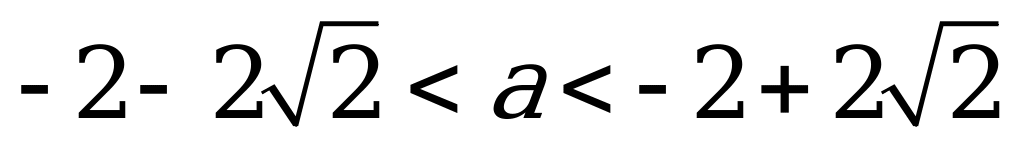
так как при 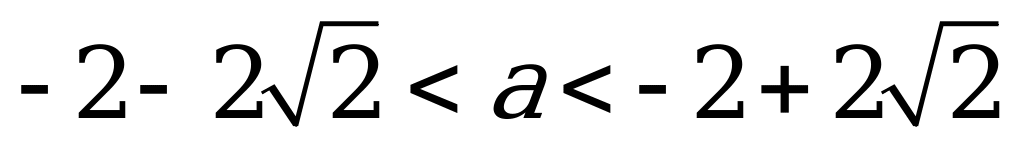 нет решений.
нет решений.
Рассмотрим теперь другой случай: 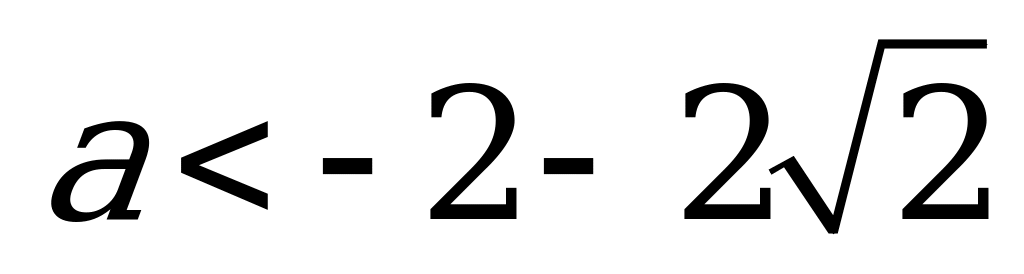 или
или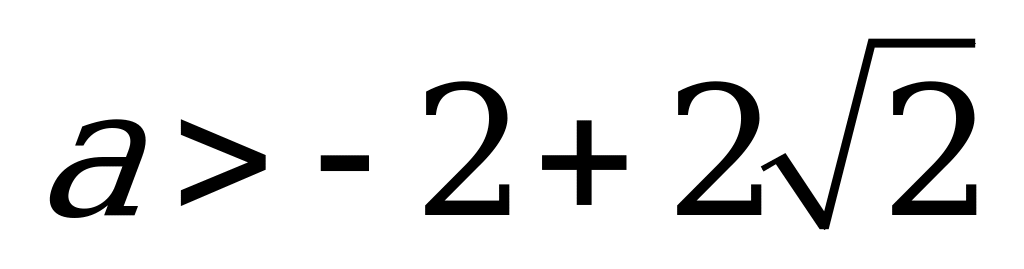
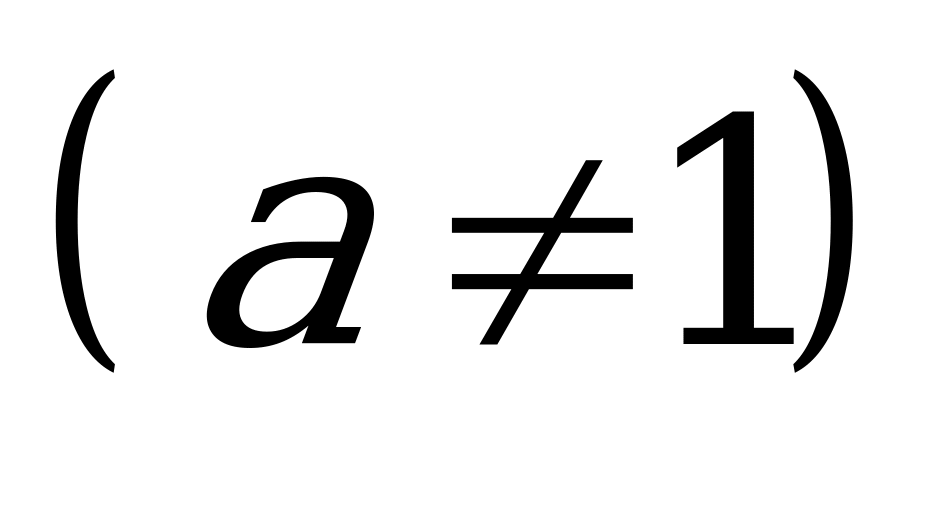 .
.
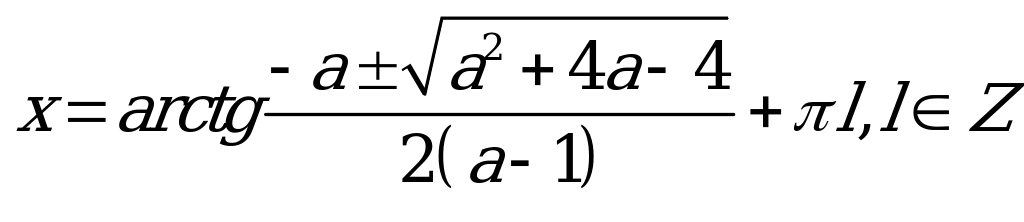
Очевидно, что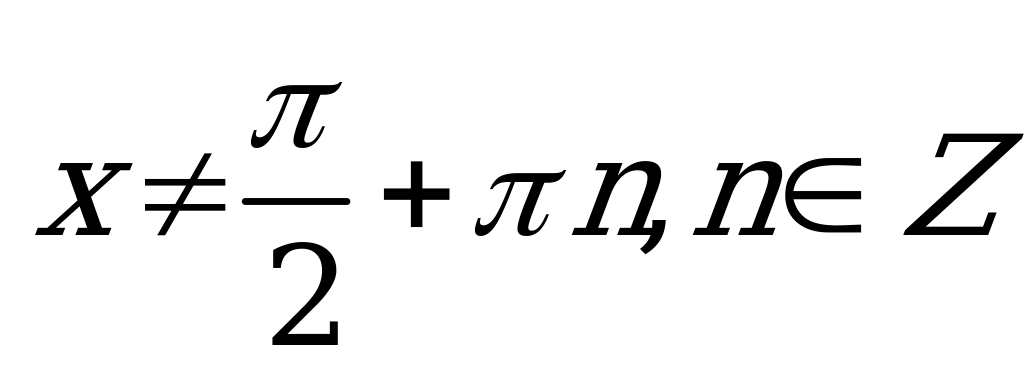 . Поэтому, учитывая
. Поэтому, учитывая 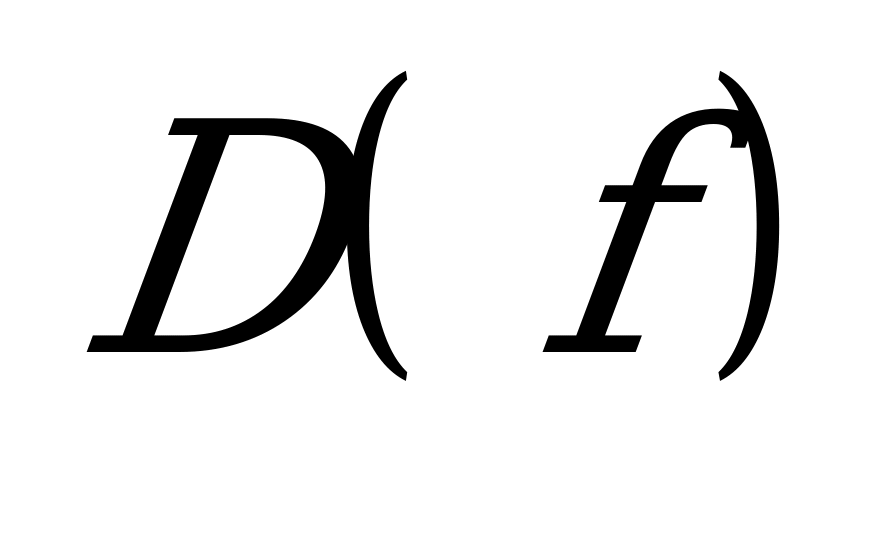 , имеем:
, имеем:
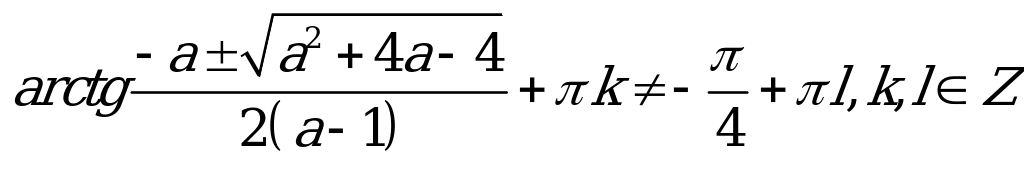
Если 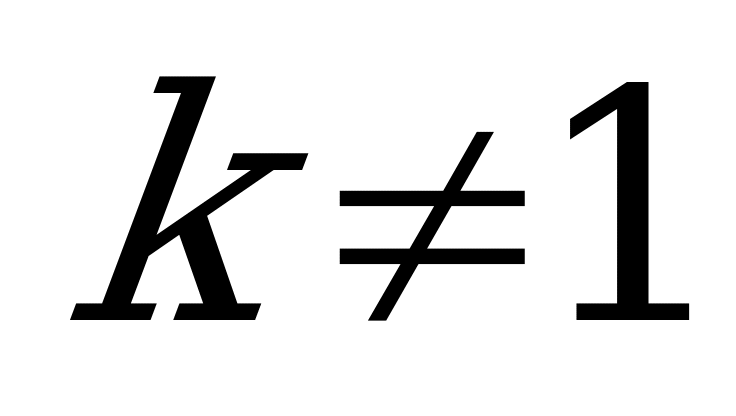 , то то это неравенство выполняться не может. Если
, то то это неравенство выполняться не может. Если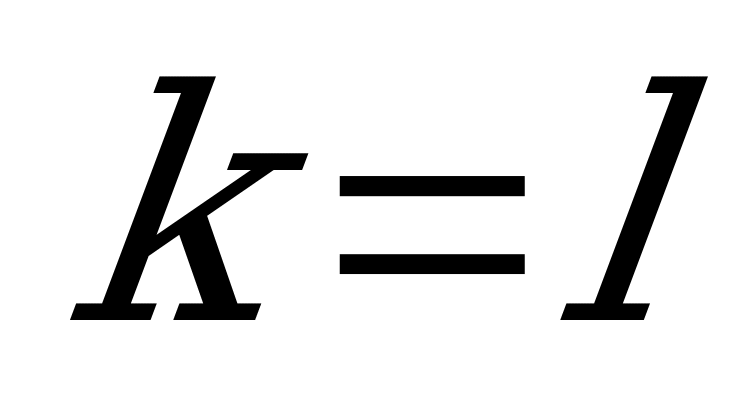 , то:
, то:
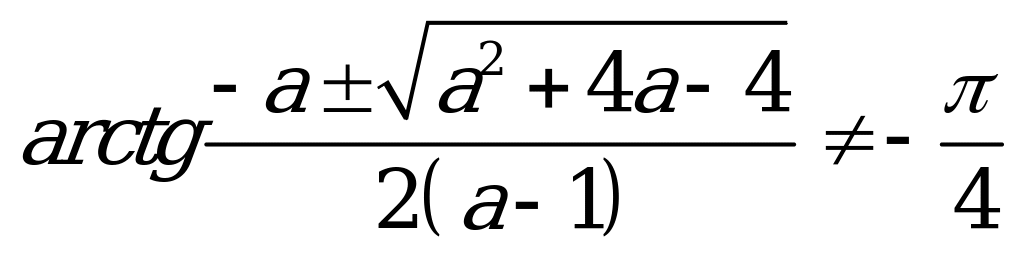 ;
; 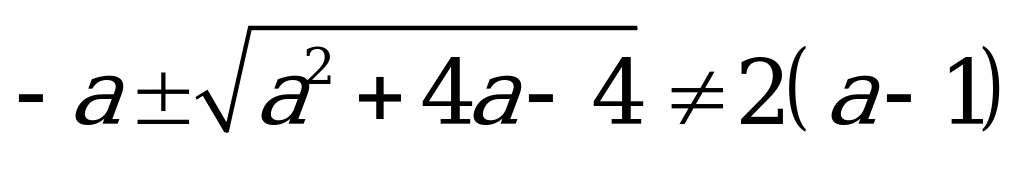
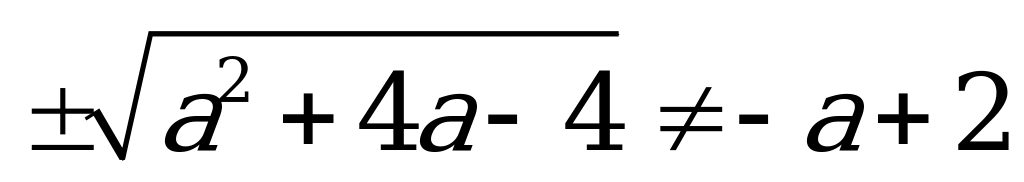 ;
; 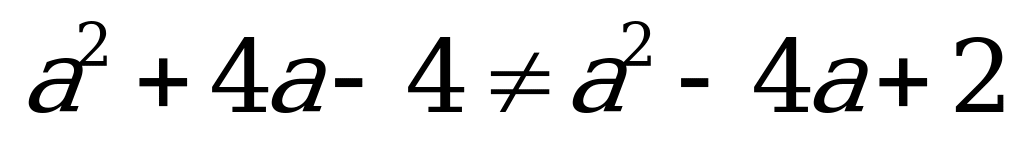
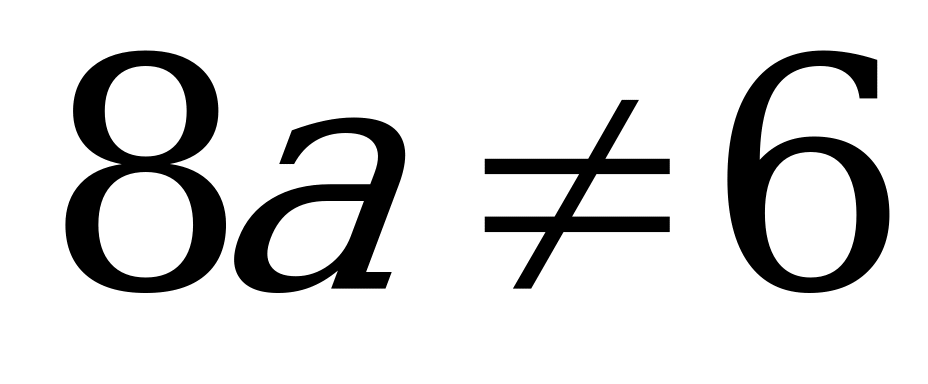 ;
; 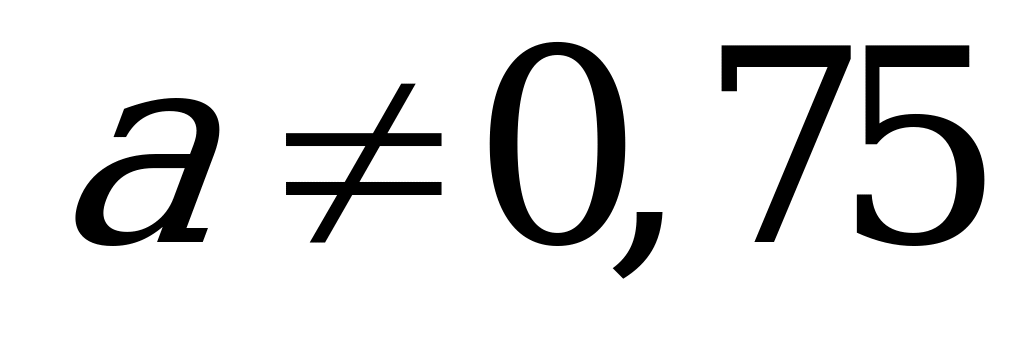
Так как 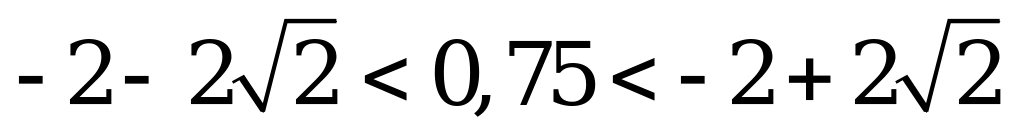 , то условие
, то условие 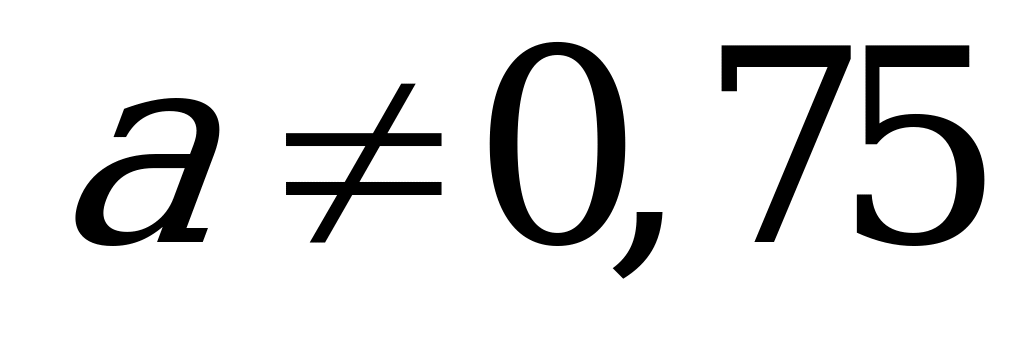 можно не учитывать.
можно не учитывать.
Ответ: При 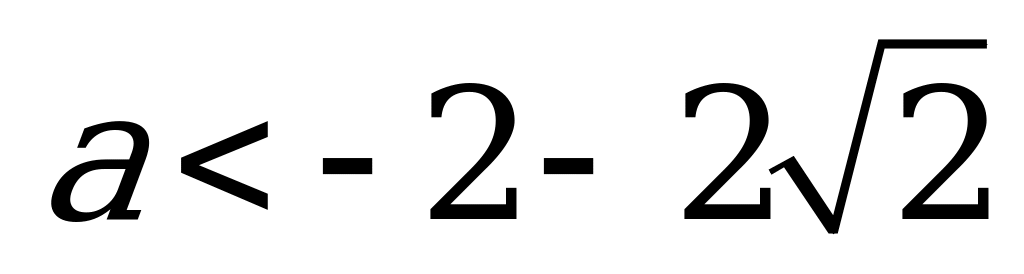 или
или 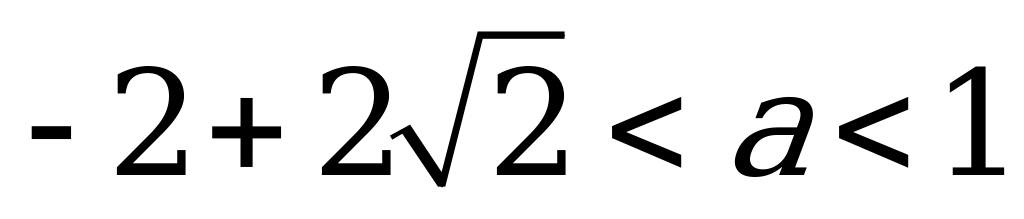 или
или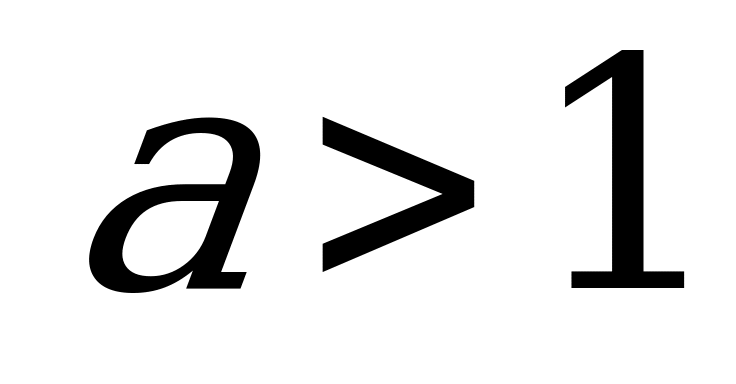 :
: 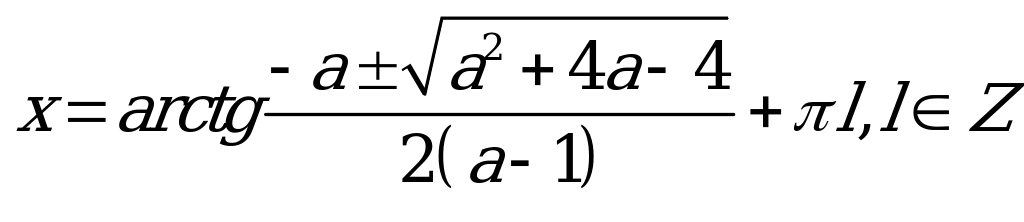
При 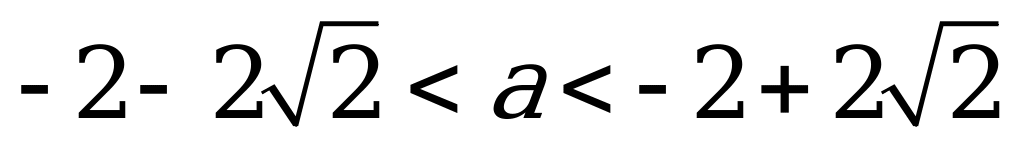 решений нет;
решений нет;
при 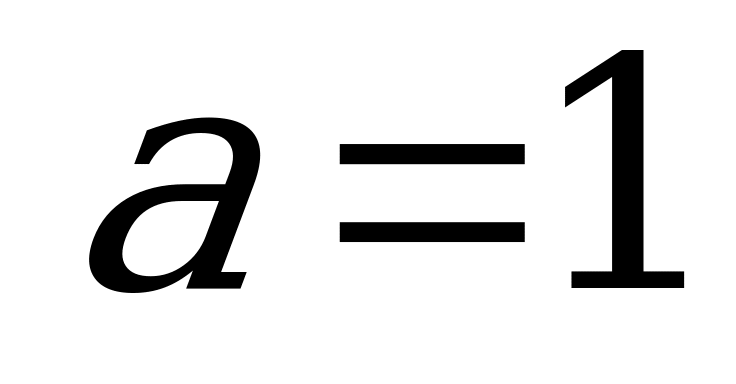 :
: 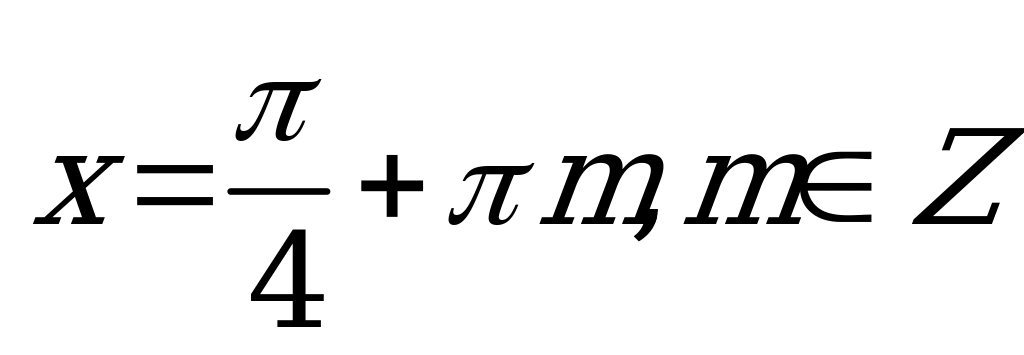 .
.
Графический способ
Решения изображаются на координатной плоскости
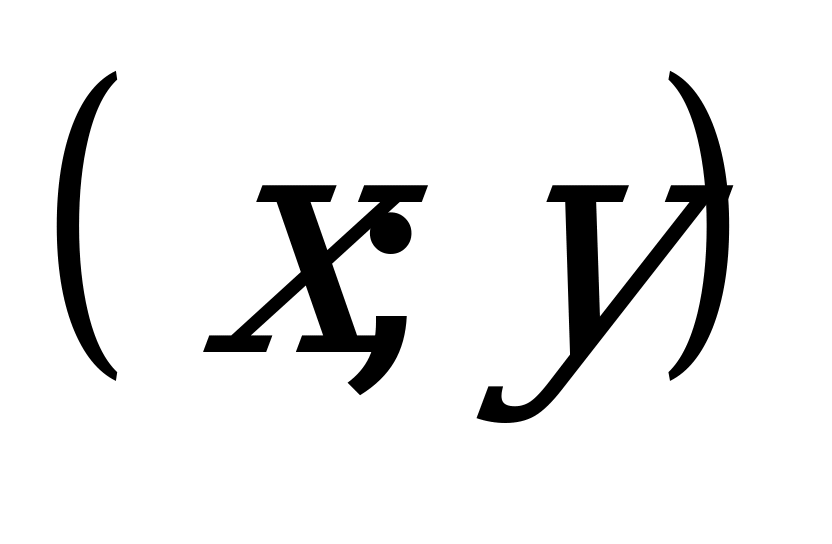
[2;4].
Пример 2. При каких значениях 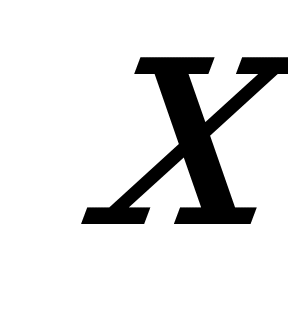 уравнение
уравнение
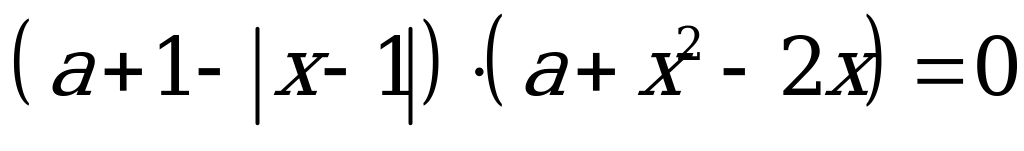
имеет три корня?
Решение:
Данное уравнение равносильно совокупности уравнений:
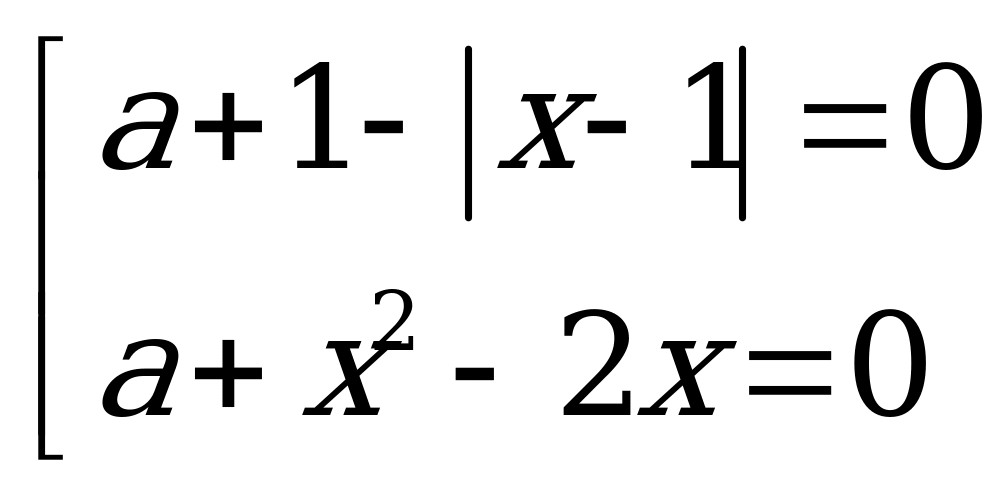
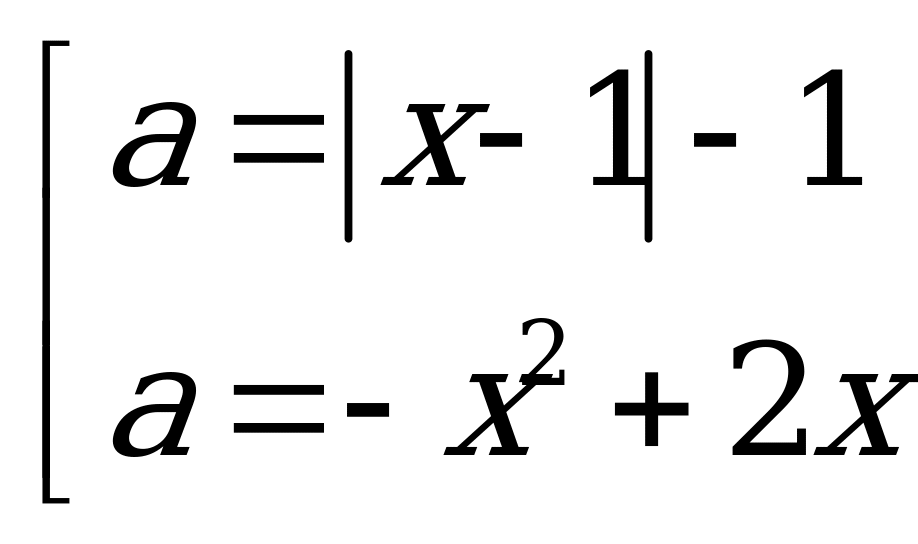
В координатной плоскости 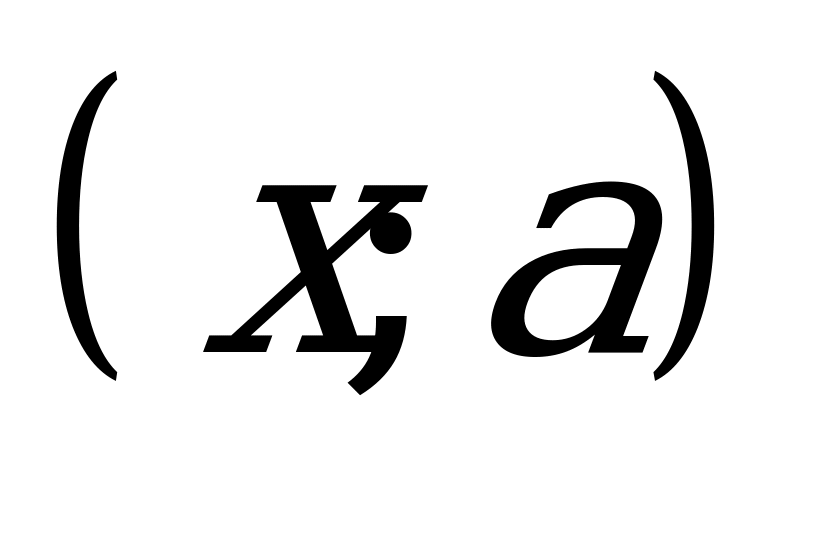 построим все графики полученных функцій:
построим все графики полученных функцій:
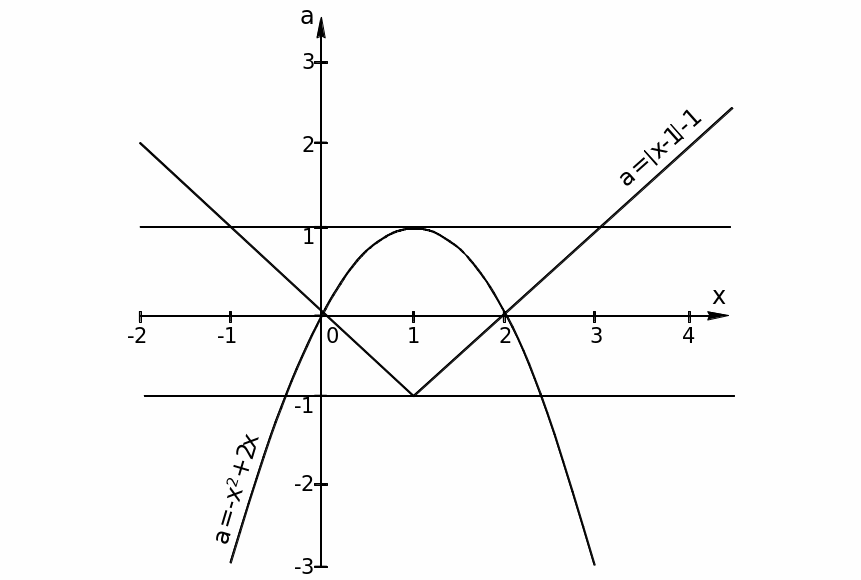
Горизонтальные прямые по условию должны иметь три точки пересечения с графиками. Таких прямых две: одна пересекает вершину параболы, отсюда 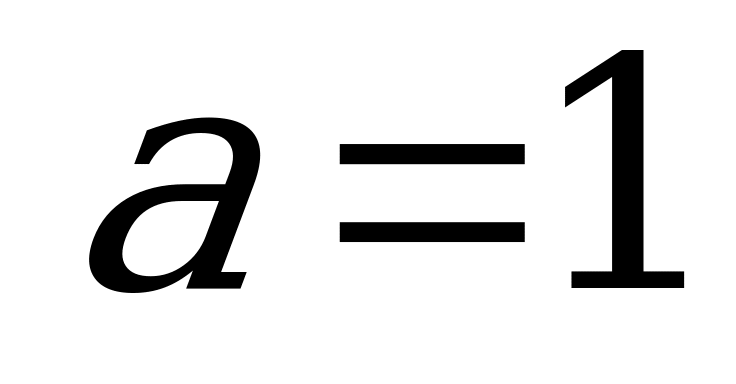 , другая – вершину «уголка», где
, другая – вершину «уголка», где 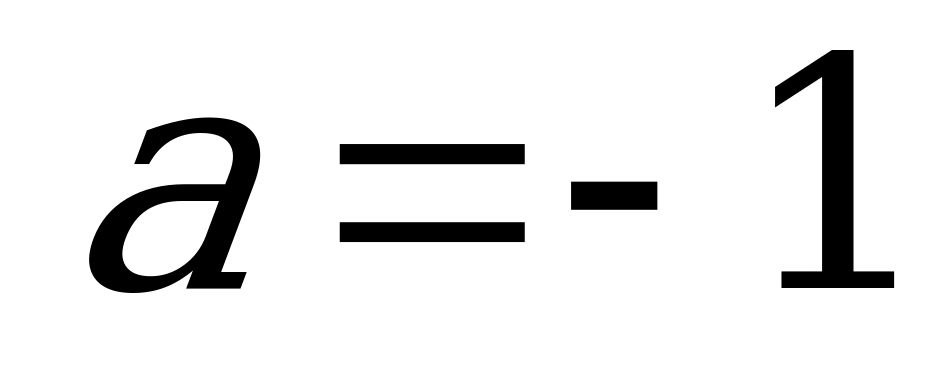 .
.
Ответ: 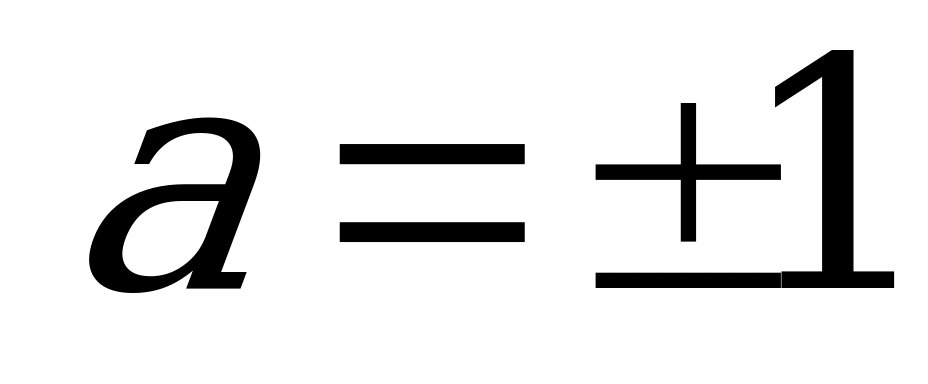 .
.
СПИСОК
ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Горбачев, В.И. Общие методы решения уравнений и неравенств с параметрами не выше второй степени / В.И. Горбачев// Математика в школе – 2000. - №2. – С. 61-68.
Епифанова, Т.Н. Графические методы решения задач с параметрами / Т.Н. Епифанова// Математика в школе – 2003. - №7. – С. 17-20.
Здоровенко, М.Ю. Учимся решать задачи с параметрами: рациональные уравнения и неравенства./ М.Ю. Здоровенко, В.М. Караулов – Киров, 1999.
Кочерова, К.С. Об уравнениях с параметром и модулем (графический способ решения) / К.С. Кочерова// Математика в школе – 1995. - №2. – С. 2-4.
Ожегов С.И. , Шведова Н.Ю. Толковый словарь русского языка. Москва. 1999.
Ястребинецкий Г.А. Задачи с параметрами: Книга для учителя. – М.: Просвещение, 1986.
7







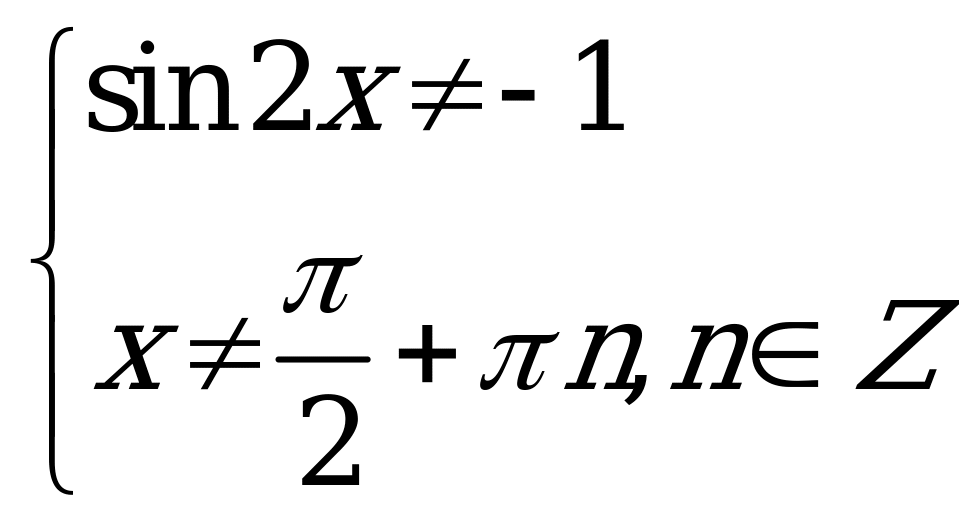 ;
;