Основные понятия теории уравнений и неравенств.
Характеризуя понятие уравнение, нужно учитывать разные стороны этого понятия. Уравнение представляет собой некоторую запись, составленную по определенным правилам (синтаксический подход). Заменяя в записи буквы (переменные) конкретными числами, имеем верные или неверные равенства (логический подход).
На практике понятие уравнения может быть введено посредствам выделения его в результате решения задач алгебраическим методом. В этом случае существенным является подход к понятию уравнения, при котором уравнение представляет косвенную форму задания некоторого неизвестного числа, имеющего в соответствии с условием конкретную математическую интерпретацию (модельный подход). Указанный способ введения понятия уравнения соответствует прикладному аспекту понятия уравнения, отраженному в следующем определении: «Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Корнем уравнения называется то значение неизвестного, при котором уравнение обращается в верное равенство».
Существует другой способ определения уравнения: «Равенство с переменной называется уравнением. Значение переменной, при котором равенство с переменной обращается в верное числовое равенство, называется корнем уравнения». Это определение характеризует уравнение как предикат особого вида, а корень уравнения – число из множества истинности этого предиката. Термин «уравнение» несет в себе признаки знакового компонента, а термин «корень уравнения» учитывает смысловой компонент.
Можно встретить и третий способ определения, роль которого проявляется при изучении графического метода решения уравнений: «Уравнение – это равенство двух функций».
Каждое из приведенных определений задают достаточно широкие классы математических объектов, к которым относятся и записи: 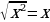 ,
, 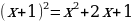 ,
, 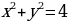 . Если первое равенство можно отнести к уравнениям особого вида, то второе – тождество, а третье – уравнение кривой. Одна и та же запись в зависимости от контекста может отражать подлежащее решению уравнение, и тождество, и уравнение кривой.
. Если первое равенство можно отнести к уравнениям особого вида, то второе – тождество, а третье – уравнение кривой. Одна и та же запись в зависимости от контекста может отражать подлежащее решению уравнение, и тождество, и уравнение кривой.
С вязь основных понятий теории уравнений отражена на рисунке 1.
вязь основных понятий теории уравнений отражена на рисунке 1.
Р
 авенство
авенство


Ч
 исловое С буквой (переменной, неизвестной)
исловое С буквой (переменной, неизвестной)




Неверное Верное Уравнение ……..

 Корень уравнения
Корень уравнения

Решить уравнение
Рис.1.
Аналогичные рассмотренным выше определениям могут быть даны неравенствам, уравнениям с несколькими неизвестными, системам уравнений и неравенств.
К лассификация уравнений и неравенств тесно связана с конкретными функциями, изучаемыми в школьном курсе математики. В соответствии с этим выделены определенные виды уравнений, представленные на рисунке 2.
лассификация уравнений и неравенств тесно связана с конкретными функциями, изучаемыми в школьном курсе математики. В соответствии с этим выделены определенные виды уравнений, представленные на рисунке 2.
У
 равнения
равнения


А
 лгебраические Неалгебраические
лгебраические Неалгебраические



Р
 ациональные Иррациональные Показательные
ациональные Иррациональные Показательные

 Логарифмические
Логарифмические
Ц
 елые рациональные Дробно рациональные Тригонометрические
елые рациональные Дробно рациональные Тригонометрические


Линейные Нелинейные


Квадратные Высших порядков
Рис.2.
Аналогичная классификация используется и для неравенств.
В отношении формирования понятия равносильности и его применения учебные пособия можно разделить на две группы. К первой относятся те пособия, в которых использование равносильных преобразований явно основано на введении и изучении понятия равносильности; ко второй – те, в которых применение равносильных преобразований предшествует определению понятия равносильности.
Методика работы над понятием при указанных подходах существенно отличается.
В школьном курсе математики можно выделить три этапа, связанных с рассмотрением этого вопроса.
Во-первых, на пропедевтическом этапе в начальном курсе математики и в начале изучения алгебры решаются простейшие модели. Используемые преобразования получают индуктивное образование. По мере накопления опыта индуктивные рассуждения чаще заменяются такими, где равносильность используется, но сам термин не вводится.
Во-вторых, выделяется понятие равносильности и сопоставляется его теоретическое содержание с правилами преобразований, которые выводятся на его основе.
В-третьих, на основе общего понятия равносильности происходит развертывание и общей теории, и теории отдельных классов уравнений и неравенств.
В процессе решения уравнений также используются понятие логического следования, которое изучается позже понятия равносильности и является дополнением к нему. Логическое следование применяется в основном тогда, когда не удается найти вариант равносильного преобразования. Реже, когда соблюдение требования равносильности приводит к громоздким преобразованиям, логическое следование используется как прием, упрощающий процесс решения.
Выделятся три основных типа преобразований.
Преобразование одной из частей уравнения или неравенства. Используется при необходимости упростить выражение в какой-то из частей уравнения или неравенства. Имеется возможность перехода к неравносильной модели. Основой преобразований данного типа являются тождественные преобразования, поэтому классифицировать их можно в соответствии с классификации тождественных преобразований (раскрыть скобки, приведение подобных слагаемых, приведение к общему знаменателю и др.).
Согласованное изменение обеих частей уравнения (неравенства). На основе основных свойств числовых равенств (неравенств) формулируются основные свойства равенств (неравенств) с одним неизвестным, например:
любой член неравенства можно перенести из одной части неравенства в другую, изменив его знак на противоположный, при этом знак неравенства не меняется;
обе части неравенства можно умножить или разделить на одно и то же число, не равное нулю; если это число положительно, то знак неравенства не меняется, а если это число отрицательно, то знак неравенства меняется на противоположный.
Преобразования, изменяющие логическую структуру. Можно выделить два подтипа:
преобразования, осуществляемые на основе свойств арифметических операций. К ним можно отнести переход от уравнения к совокупности уравнений после предварительного разложения на множители; переход от уравнения к системе после приравнивания суммы квадратов выражений к нулю; почленное сложение, умножение, деление уравнений, неравенств и т.д.;
преобразования, осуществляемые при помощи логических операций. Примерами их являются выделение из системы одного из компонентов, замена переменных.







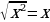 ,
, 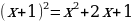 ,
, 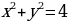 . Если первое равенство можно отнести к уравнениям особого вида, то второе – тождество, а третье – уравнение кривой. Одна и та же запись в зависимости от контекста может отражать подлежащее решению уравнение, и тождество, и уравнение кривой.
. Если первое равенство можно отнести к уравнениям особого вида, то второе – тождество, а третье – уравнение кривой. Одна и та же запись в зависимости от контекста может отражать подлежащее решению уравнение, и тождество, и уравнение кривой. вязь основных понятий теории уравнений отражена на рисунке 1.
вязь основных понятий теории уравнений отражена на рисунке 1.
 авенство
авенство
 исловое С буквой (переменной, неизвестной)
исловое С буквой (переменной, неизвестной)




 Корень уравнения
Корень уравнения лассификация уравнений и неравенств тесно связана с конкретными функциями, изучаемыми в школьном курсе математики. В соответствии с этим выделены определенные виды уравнений, представленные на рисунке 2.
лассификация уравнений и неравенств тесно связана с конкретными функциями, изучаемыми в школьном курсе математики. В соответствии с этим выделены определенные виды уравнений, представленные на рисунке 2.
 равнения
равнения

 лгебраические Неалгебраические
лгебраические Неалгебраические

 ациональные Иррациональные Показательные
ациональные Иррациональные Показательные
 Логарифмические
Логарифмические
 елые рациональные Дробно рациональные Тригонометрические
елые рациональные Дробно рациональные Тригонометрические