«10 задач для подготовки к Всероссийской олимпиаде школьников по математике»
7 класс.
Условия задач.
1. Расставьте скобки, чтобы равенство стало верным: 0,5 + 0,5 : 0,5 + 0,5: 0,5 = 5.
2. На листке написано выражение: 4 − 5− 7 −11−19 = 22. Расставьте знаки модуля так, чтобы получилось верное равенство.
3. Замените буквы цифрами так, чтобы получилось верное равенство: ГОЛ * ГОЛ = ФУТБОЛ,
если известно, что одинаковые буквы соответствуют одинаковым цифрам, разные – разным.
4. Сократите дробь:  .
.
5. Из натурального числа вычли сумму его цифр и получили 2016. Найдите наибольшее возможное исходное число.
6. В ящике 24 кг гвоздей. Как на чашечных весах без гирь и без стрелки отмерить 9 кг?
7. Пять кошек и четыре котёнка весят 19 кг. Четыре кошки и пять котят весят 17 кг. Сколько весит кошка и сколько весит котёнок?
8. Маугли попросил своих друзей-обезьян принести ему орехов. Обезьяны набрали поровну орехов и понесли Маугли. Но по дороге они поссорились, и каждая обезьяна бросила в каждую по ореху. В результате Маугли досталось лишь 35 орехов. Сколько орехов собрали обезьяны, если известно, что каждая из них принесла больше одного ореха?
9. Нарисовать треугольник, который можно разделить на 5 равных треугольников.
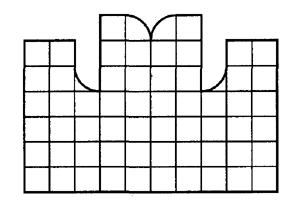
10. На рисунке изображена часть крепостной стены. Один из камней имеет столь причудливую форму, что если его вытащить из стены и положить иначе, то стена станет ровной. Изобразите этот камень.
Ответы и решения задач:
1. Расставьте скобки, чтобы равенство стало верным: 0,5 + 0,5 : 0,5 + 0,5: 0,5 = 5.
Ответ: ((0,5 + 0,5) : 0,5 + 0,5) : 0,5 = 5 .
2. На листке написано выражение: 4 − 5− 7 −11−19 = 22. Расставьте знаки модуля так, чтобы получилось верное равенство.
Решение: | |4 – 5| −| 7 −11−19|| = 22. Ответ: 22.
3. Замените буквы цифрами так, чтобы получилось верное равенство: ГОЛ * ГОЛ = ФУТБОЛ,
если известно, что одинаковые буквы соответствуют одинаковым цифрам, разные – разным.
Решение:
425 • 425 = 180625.
Ответ: Б – 6, Г – 4, Л – 5, О 2, Т 0, У 8, Ф 1.
4. Сократите дробь:  .
.
Решение:  . Ответ:
. Ответ: .
.
5. Из натурального числа вычли сумму его цифр и получили 2016. Найдите наибольшее возможное исходное число.
Решение:
Исходное число не может быть двух- и трёхзначным, так как в этом случае разность числа и суммы его цифр будет значительно меньше, чем 2016. Не может оно быть и пятизначным, так как в этом случае разность числа и суммы его цифр будет значительно больше, чем 2016. Выходит, искомое число четырёхзначное.
Представим искомое число как  = 1000a + 100b + 10c + d.
= 1000a + 100b + 10c + d.
Если мы вычтем из него сумму его цифр, то получим
1000a +100b +10c + d −(a +b +c +d) = 999a + 99b +9c = 9(111a + 11b + c) = 2016.
Тогда 111a + 11b + c = 2016 : 9 = 224.
Очевидно, что a не может быть равно 3 и больше (111• 3 = 333).
Также a ≠0, a≠1.
Даже если b и c имеют максимально возможные значения (то есть 9), равенства не получается: 111 • 0 + 11 • 9 + 9 = 108, а 111•1+ 11 • 9 + 9 = 219. Значит, a = 2.
В этом случае b не может быть равно единице и больше, т.к. 111•2+11•1=244. Значит, b = 0, отсюда с = 2. При этом d может быть любым. Максимальным исходное число будет при d = 9, то есть искомое число равно 2029.
Ответ: 2029.
6. В ящике 24 кг гвоздей. Как на чашечных весах без гирь и без стрелки отмерить 9 кг?
Решение:
Разделим 24 кг на две части, отмерив на весах по 12 кг гвоздей. Отложим одну кучу гвоздей, а вторую поделим поровну. Получим две кучи по 6 кг. Одну из них поделим пополам. Всего у нас будет четыре кучи гвоздей по 12, 6, 3, 3 кг. Сложим вторую и третью, получим ровно 9 кг.
7. Пять кошек и четыре котёнка весят 19 кг. Четыре кошки и пять котят весят 17 кг. Сколько весит кошка и сколько весит котёнок?
Решение:
5 кошек + 4 котенка = 19 кг
4 кошки + 5 котят = 17 кг.
Значит, кошка тяжелее котенка на 19 - 17 = 2 кг.
Зная это, заменим при первом взвешивании всех 5 кошек котятами:
у нас тогда будет 5 + 4 = 9 котят, а стрелка весов, вместо 19 кг, покажет на 2 • 5=10 кг меньше (т.к. масса котенка на 2 кг. меньше массы кошки).
Значит, 9 котят весят 19 - 10 = 9 кг.
Отсюда ясно, что котенок весит 1 кг, а взрослая кошка 1 + 2 = 3 кг.
Ответ: котенок весит 1кг, кошка – 3 кг.
8.Маугли попросил своих друзей-обезьян принести ему орехов. Обезьяны набрали поровну орехов и понесли Маугли. Но по дороге они поссорились, и каждая обезьяна бросила в каждую по ореху. В результате Маугли досталось лишь 35 орехов. Сколько орехов собрали обезьяны, если известно, что каждая из них принесла больше одного ореха?
Решение:
Так как обезьяны собрали орехов поровну и поровну бросили, то принесли они поровну. Имеем 35 = 5∙7 . Возможны два случая:
1) обезьян было 5, принесли по 7, бросили по 4 ореха, значит, каждая собрала 11 = 7 + 4; 2) обезьян было 7, принесли по 5, бросили по 6 орехов, значит, каждая собрала 11 = 5+ 6 .
Ответ: 11 орехов
9. Нарисовать треугольник, который можно разделить на 5 равных треугольников.
Решение:
Очевидно, что треугольник можно разделить на 4 равные части. Далее к этому треугольнику требуется «приставить» его четвертую часть, при этом снова должен получиться треугольник. Это возможно только в том случае, когда треугольник является прямоугольным, так как только тогда сумма двух прямых углов даст развернутый угол (отрезок, который является стороной треугольника, при этом будет суммой сторон большого треугольника и его «четвертушки»).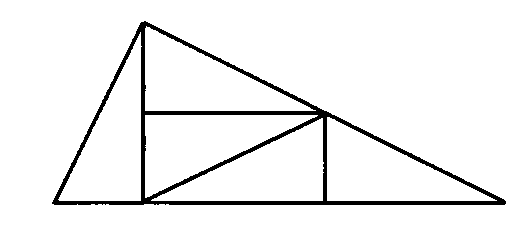
5. На рисунке изображена часть крепостной стены. Один из камней имеет столь причудливую форму, что если его вытащить из стены и положить иначе, то стена станет ровной. Изобразите этот камень.
Решение:
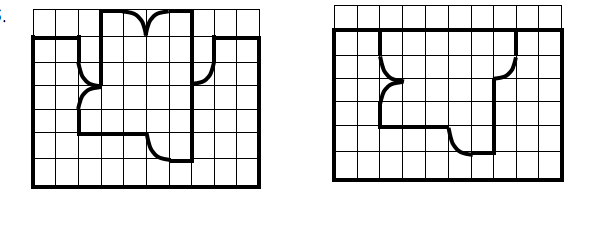







 .
. 
 . Ответ:
. Ответ: .
. = 1000a + 100b + 10c + d.
= 1000a + 100b + 10c + d.











