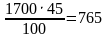Десятичные дроби и проценты.

Урок _________

Тема: Десятичные дроби и проценты

Цель: Повторить действия с десятичными дробями; нахождение процента величины и величины по ее проценту; переход от процентов к десятичным дробям и от дробей к процентам; расширить знания учащихся о процентах. совершенствовать навыки решения задач на проценты.

Развивать вычислительные навыки, умение логически излагать мысль, совершенствовать навыки решения задач на проценты, чувство товарищества.

Воспитывать активность, аккуратность, трудолюбие, чувство ответственности.

Цели урока: добиться предметных, личностных и метапредметных результатов:

Предметный результат –

• овладеть математическими знаниями и умениями при переводе % в десятичные дроби и наоборот;

Личностный результат-

• развитие логического и критического мышления, куль­туры речи;

• развитие математических способностей через творчекую работу;

Метапредметный результат -

• формирование общих способов интеллектуальной дея­тельности, характерных для математики и устнго народного творчества, являющихся осно­вой познавательной культуры ученика;

Задачи формирования УУД:

Познавательные УУД:

- умение формулировать тему и проблему урока;

- умение добывать новые знания, находить ответы на поставленные вопросы;

– делать выводы в результате совместной работы класса и учителя;

Коммуникативные УУД:

- развивать умение слушать и понимать речь других, высказывать свое мнение и аргументировать свой ответ;

- осуществлять совместную познавательную деятельность в группах;

- оформлять свои мысли в устной форме;

Личностные УУД:

- развивать умение высказывать свое отношение к полученной информации;

- развитие ма­тематических способностей обучающихся;

Регулятивные УУД:

- умение определять цель деятельности на уроке (собственная целевая установка);

- умение проговаривать последовательность действий на уроке;

- умение подводить итоги своей деятельности на уроке;

- умение оценивать свои учебные действия;

Тип урока: формирование новых знаний.

Ход урока

1. 0,7 ˑ 10 : 2 - 0,3 : 0,4	4 - 0,8 : 0,8 : 10 ˑ 0,5	40 ˑ 0,4 : 10 + 0,5 : 7	4,2 + 4,8 : 5 : 3 - 0,5
   ?	?	?	?

   Организационный момент

1. Приветствие

2. Проверка готовности к уроку

1. Актуализация знаний

1. Вычислите устно:

1. Денежная единица нашей страны…(рубль)

2. Долю 1/2 называют…(половиной)

3. Самая низкая оценка, но её редко ставят …(единица)

4. Любые две точки можно соединить только одним…(отрезком)

5. Главная точка окружности…(центр)

6. 103 (тысяча)

7. Единственная цифра, которая не является натуральным числом…(ноль)

Из первых букв верных ответов получилась такая анаграмма:

Р П Е О Ц Т Н. (буквы - на карточках)

Расшифруйте её, т. е. составьте слово из этих букв. Получилось слово процент. Это и есть тема нашего урока, а точнее - проценты.

В школе учитель за ваши дела
Ставит в журнале оценки.
Сотую долю любого числа
Мы называем…( процентом)

1. Фронтальный опрос:

Чтобы перейти к решению задач, давайте вспомним некоторые правила и рассмотрим примеры.

1) Выразите проценты обыкновенной дробью: 1%, 7%, 13%, 100%.
Сформулируйте правило, как выразить проценты обыкновенной дробью.

2) Как выразить проценты десятичной дробью?
Приведите примеры.

После ответа учащихся на доске прикрепляется табличка:

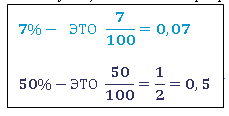
3) Вспомним правило нахождения процентов от числа.

Пример: найти 32% от числа А

После ответа учащихся на доске прикрепляется табличка:

1) представьте проценты в виде десятичной дроби: 1 %, 17 %, 25 %, 30 %, 100 %, 175 %, 0,8 %,

2) выразите дробь в виде процента: 0,7; 0,3; 0,37; 1; 1,27; 0,906; 3,457.

3) Какую часть числа составляют 50 % этого числа; 25 % этого числа; 10 % этого числа?

1. Мотивация.

Проценты – это одна из сложнейших тем математики. Понимание процентов и умение выполнять процентные расчеты, необходимы для каждого человека. Прикладное значение этой темы велико и затрагивает различные сферы деятельности человека. Задачи на процентные расчеты часто приходится решать людям, которые в своей профессии связаны с экономикой, банковским делом.

Давайте, подумаем, где применяются проценты в нашей жизни?

Проценты в нашей жизни

Как вы думаете, чем мы будем сегодня заниматься на уроке?

Какова цель нашего урока?

Давайте вспомним, какие типы задач на проценты мы знаем, какими методами можем решать задачи на проценты и приступим к решению задач: (ответы учащихся)

1. Формирование умений и навыков

№ 1 (решить задачу тремя способами) - работа в парах

В школе 1700 учащихся, из них 45 % девочки. Сколько девочек в школе?

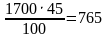№ 866

Число 200увеличили на 20 %, полученный результат уменьшили на 20 %. Получится ли в результате число 200? Какое число получится?

Решение:

1) 1,2 ˑ 200 = 240 – стало;

2) 240 ˑ 0,2 = 48 – составляет 20% от 240;

3) 240 – 48 = 192 число.

Физкультминутка

№ 879 (фронтально)

Имеется 600 г раствора, содержащего 15 % соли. Сколько воды требуется добавить в раствор, чтобы он стал содержать 10 % соли?

Решение:

1) 600 ˑ 0,15 = 90 (г) – соли содержится;

2) 90 : 0,1 = 90 (г) – раствора должно получиться;

3) 900 – 600 = 300(г) – воды надо добавить.

№ 873 (устно)

Служащая фирмы сказала: «Производство продукции нашей фирмы увеличится на 200 %, или в 2 раза». Исправьте её ошибку, если верно условие: а) на 200 %; б) в 2 раза.

Решение:

а) если производство увеличивается на 200 %, то оно теперь составляет 100% +200 % = 300% - увеличение в 3 раза.

б) если производство увеличилось в 2 раза, то оно составило 100 % ˑ 2 = 200 % от первоначального количества производимой продукции. Увеличение составило: 200 – 100 = 100 (%)

№ 868 (устно)

а) Число а больше числа b в 1,25 раза; в 1,32 раза; в 1,5 раза. На сколько процентов число а больше числа b?

б) Число а больше числа b на 25 %; на 48 %; на 60 %. Во сколько раз число а больше числа b?

(Ответ: а) 25%; 32%; 50%; б) в 1,25 раз; в 1,48 раз; в 1,6 рваз)

Дополнительная задача № 1:

В магазин поступили книги по цене 101,5 р. Наценка магазина составляет 20 %. При оптовой покупке делается скидка 5 %. Какой будет цена книжки при оптовой покупке?

Решение:

1) 101,5 ˑ 0,2 = 20,3 (р.) – наценка;

2) 101,5 + 20,3 = 121,8 (р.) – стоимость книги в магазине;

3) 121,8 ˑ 0,95 = 115,71 (р.) – цена книги при оптовой покупке.

Дополнительная задача № 2:

Вкладчик внес в банк 60 000 р. Под 12 % годовых, через год процентная ставка выросла до 15 %. Сколько денег получит вкладчик через 2 года?

Решение:

1) 60 000 ˑ 0,12 = 720 (р.) –составляет 12 %;

2) 60 000 + 720 = 60 720 (р.) на счету через год;

3) 607020 ˑ 1,15 = 69828 (р) – через два года.

1. Итог урока

Сегодня мне на уроке было (использование смайликов):

- интересно; - некомфортно; - сложно

Составить синквейн (пятистишье) сенкан

1. тема: проценты (название понятия)

2. описание темы 2 слова (прилагательные) сотые, цифровые

3. описание действия 3 словами: используются, применяются, подсчитываются

4. фраза 4 слова, которая выражает отношение к теме: обозначение доли чего-либо по отношению к целому

5. синоним: доля

1. Домашнее задание: решить № 867 (а), № 880, № 884. Повторить п. 1.6, п. 1.7 п. 4.7.
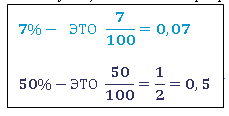