Методическая разработка "Понятие вероятности"

АЛГЕБРА

9

класс

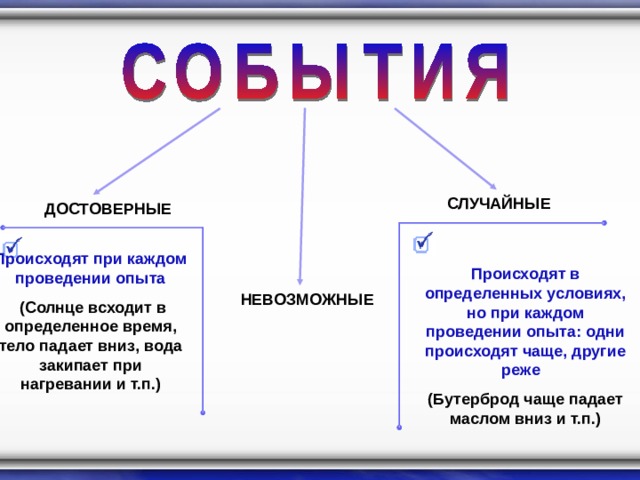
СЛУЧАЙНЫЕ

ДОСТОВЕРНЫЕ

Происходят при каждом проведении опыта

(Солнце всходит в определенное время, тело падает вниз, вода закипает при нагревании и т.п.)

Происходят в определенных условиях, но при каждом проведении опыта: одни происходят чаще, другие реже

(Бутерброд чаще падает маслом вниз и т.п.)

НЕВОЗМОЖНЫЕ

ТЕСТ

1

2

3

4

5

6

7

8

9

10

• О каком событии идёт речь?

«Из 25 учащихся класса двое справляют

день рождения 30 февраля»

А) достоверное; В) невозможное; С) случайное

2. Это событие является

случайным:

А) слово начинается с буквы«ь»

В) ученику 9 класса 14 месяцев

С) бросили две игральные

кости: сумма выпавших на

них очков равна 8

3. Найдите достоверное

событие:

А) На уроке математики ученики

делали физические упражнения

В) Сборная России по футболу не

станет чемпионом мира 2005 года

С) Подкинули монету и она упала

на «Орла»

4. Среди пар событий, найдите

несовместимые.

А) В сыгранной Катей и Славой

партии шахмат, Катя проиграла и

Слава проиграл

В) Из набора домино вынута одна

костяшка, на ней одно число очков больше 3, другое число 5

С) Наступило лето, на небе ни облачка

5. Охарактеризуйте случайное

событие:

«новая электролампа не загорится»

Это событие:

А) менее вероятно

В) равновероятное

С) более вероятное

6. Какие события из

перечисленных ниже являются

противоположными?

В колоде карт лежат четыре туза и четыре короля разных мастей. Достают карту наугад

Событие:

А) достанут трефового туза

В) достанут туза любой масти

С) достанут любую карту кроме

трефового туза

7. Колобок катится по лесным тропкам

куда глаза глядят. На полянке его

тропинка расходится на четыре тропинки, в конце которых

Колобка поджидают

Заяц, Волк, Медведь и Лиса

Сколько исходов для выбора Колобком наугад одной из четырёх тропинок

А) 1 В) 4 С) 5

8. Два стрелка делают по одному

выстрелу в мишень.

Сколько исходов двух совместных

выстрелов?

А) 4 В) 3 С) 2

9. Два шахматиста играют подряд

две партии.

Сколько исходов у этого события?

А) 4 В) 2 С) 9

10*. Случайный опыт состоит в

выяснении пола детей в семьях с

тремя детьми.

Сколько возможных исходов у этого опыта?

А) 8 В) 9 С) 6

В толковом словаре С.И. Ожегова и Н.Ю. Шведовой:

«Вероятность – возможность исполнения, осуществимости чего-нибудь»

Основатель современной теории вероятностей А.Н.Колмогоров:

«Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях»

Известно, по крайней мере, шесть основных схем определения и понимания вероятности . Не все они в равной мере используются на практике и в теории, но, тем не менее, все они имеют за собой разработанную логическую базу и имеют право на существование

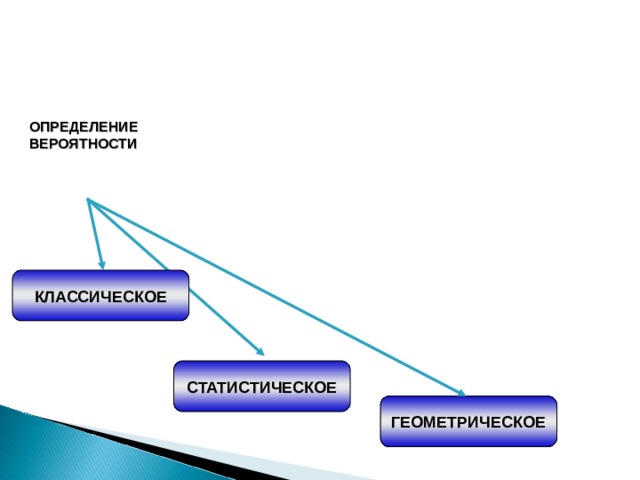
ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

КЛАССИЧЕСКОЕ

СТАТИСТИЧЕСКОЕ

ГЕОМЕТРИЧЕСКОЕ

– ЭТО ЧИСЛЕННАЯ МЕРА ОБЪЕКТИВНОЙ ВОЗМОЖНОСТИ ПОЯВЛЕНИЯ СЛУЧАЙНОГО СОБЫТИЯ

ТЕОРИЯ ВЕРОЯТНОСТЕЙ ДАЕТ СПОСОБ НАХОЖДЕНИЯ ЧИСЛЕННОГО ЗНАЧЕНИЯ ВЕРОЯТНОСТИ СОБЫТИЯ:

А – некоторое событие

m – количество исходов, при которых событие А появляется

n – конечное число равновозможных исходов

P – обозначение происходит от первой буквы французского слова probabilite – вероятность

КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

Вероятностью Р наступления случайного события А называется отношение , где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов:

Классическое определение вероятности было впервые дано в работах французского математика Лапласа

Пьер-Симо́н Лапла́с

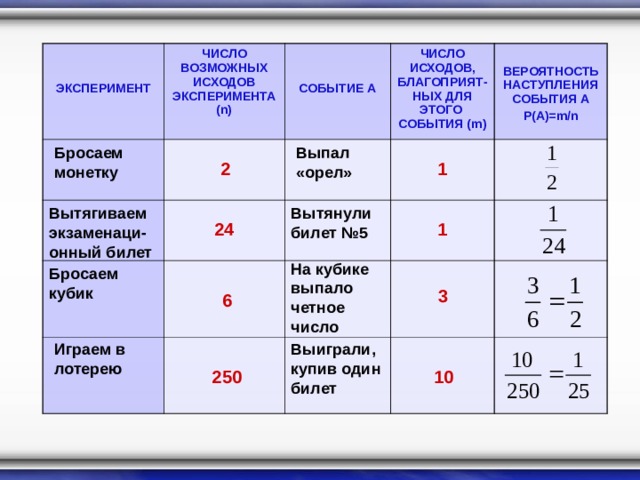
ЭКСПЕРИМЕНТ

ЧИСЛО ВОЗМОЖНЫХ ИСХОДОВ ЭКСПЕРИМЕНТА ( n)

СОБЫТИЕ А

ЧИСЛО ИСХОДОВ, БЛАГОПРИЯТ- НЫХ ДЛЯ ЭТОГО СОБЫТИЯ ( m)

ВЕРОЯТНОСТЬ НАСТУПЛЕНИЯ СОБЫТИЯ А

Р(А)= m / n

Бросаем монетку

Выпал «орел»

2

1

Вытягиваем экзаменаци- онный билет

Вытянули билет №5

24

1

На кубике выпало четное число

Бросаем кубик

3

6

Играем в лотерею

Выиграли, купив один билет

250

10

В школе 1300 человек, из них 5 человек хулиганы.

Какова вероятность того, что один из них попадётся директору на глаза?

Вероятность:

P ( A ) = 5/1300 = 1/250

При игре в нарды бросают 2 игральных кубика.

Какова вероятность того, что на обоих кубиках выпадут одинаковые числа?

Составим следующую таблицу

1

1

2

11

2

3

12

21

3

31

22

4

4

13

5

32

14

5

41

23

24

6

42

51

33

6

15

52

34

16

43

25

61

26

53

44

35

62

54

36

45

63

55

64

46

56

65

66

Вероятность: P(A)=6/36 = = 1/6

Из карточек составили слово «статистика».

Какую карточку с буквой вероятнее всего вытащить ? Какие события равновероятные ?

Всего 10 букв

Буква «с» встречается 2 раза –

P (с) = 2 / 10 = 1 / 5

Буква «т» встречается 3 раза –

P( т) = 3 / 10

Буква «а» встречается 2 раза –

P( а) = 2 / 10 = 1 / 5

Буква «и» встречается 2 раза –

P( и) = 2 / 10 = 1 / 5

Буква «к» встречается 1 раз –

P( к) = 1 / 10

Свойства вероятности

• Вероятность достоверного события равна

• Вероятность невозможного события равна

• Вероятность события А не меньше , но не больше

?

1

?

0

?

?

1

0

• P(u) = 1 ( u – достоверное событие)
• P(u) = 1 ( u – достоверное событие)

• P(v) = 0 ( v – невозможное событие)
• P(v) = 0 ( v – невозможное событие)

• 0  P(A)  1
• 0  P(A)  1

Самостоятельная работа

Задача 1

В коробке 4 синих, 3 белых и 2 желтых фишки. Они тщательно перемешиваются, и наудачу извлекается одна из них.

Найдите вероятность того, что она окажется:

а) белой ; б) желтой ; в) не желтой . 

а) Мы имеем всевозможных случаев 9 . Благоприятствующих событий 3 . Вероятность равна:

P=3:9=1/3=0,33(3)

б) Мы имеем всевозможных случаев 9 . Благоприятствующих событий 2 . Вероятность равна P=2:9=0,2(2)

в) Мы имеем всевозможных случаев 9 . Благоприятствующих событий 7 ( 4+3 ). Вероятность равна P=7:9=0,7(7)

Задача 2

Мальчики играли в “Орлянку”. Но монетка куда-то закатилась.

Предложите, как заменить ее игральным кубиком?

Считать:

"орел" -  четное число

"решка" - нечетное число

Задача 3

Какую справедливую игру можно предложить двум девочкам , у которых есть 3 красных и 1 белый шарик и мешок?

Всевозможных событий 6

(красный № 1 - красный № 2 ;

красный № 1 - белый;

красный № 2 - белый;

красный № 3 - красный № 2 ;

красный № 3 - красный № 1 ;

красный № 3 - белый)

Из них благоприятных 3 .

Выигрывает тот, кто вытаскивает 2 красных шара.

Задача 4

В настольной игре сломалась вертушка с тремя разными секторами: красным , белым и синим , но есть кубик.

Как заменить вертушку? 

Считать на кубике:

1 и 2 - красный сектор

3 и 4 - синий сектор

5 и 6 - белый сектор

Литература:

• Бунимович Е.А., Булычев В.А. Вероятность и статистика в курсе математики общеобразовательной школы . Лекции. – М.: Педагогический университет, 2005

2. Бунимович Е.А., Булычев В.А. Основы статистики и вероятности 5-11 кл. – М.: Дрофа, 2008

3. Бунимович Е.А., Булычев В.А. Вероятность и статистика в курсе математики основной школы. Лекция 1. – Приложение «Математика» к газете «1 сентября». Лекторий, №17/2007