
Отгадав ребус,
вы узнаете тему
нашего урока.


Цель урока:
Научиться строить график квадратичной функции, заданной формулой и отработать алгоритм при построении графиков квадратичной функции.

Задачи урока:
- проверить знания, умения и навыки построения графика квадратичной функции, заданной формулой;
- внедрить алгоритм построения графика квадратичной функции, заданной формулой отработать алгоритм при построении графиков квадратичной функции.
 0 ветви параболы у = ах 2 направлены … . вверх Если а о и х 0, то функция у = ах 2 принимает … (положительные, отрицательные) значения. отрицательные" width="640"
0 ветви параболы у = ах 2 направлены … . вверх Если а о и х 0, то функция у = ах 2 принимает … (положительные, отрицательные) значения. отрицательные" width="640"
Заполни пропуски …
1. Функция у = a х 2 + bx + c, где а, b, c – заданные действительные числа, а 0, х – действительная переменная, называется … функцией.
квадратичной
2. График функции у = ах 2 при любом а 0 называют … .
параболой
3. Функция у = х 2 является … (возрастающей, убывающей) на промежутке х 0.
убывающей
4. Значения х, при которых квадратичная функция равна нулю, называют … функции.
нулями функции
5. Точку пересечения параболы с осью симметрии называют … параболы.
вершиной параболы
6. При а 0 ветви параболы у = ах 2 направлены … .
вверх
- Если а о и х 0, то функция у = ах 2 принимает …
(положительные, отрицательные) значения.
отрицательные
 0, то ветви направлены вверх a , то ветви направлены вниз" width="640"
0, то ветви направлены вверх a , то ветви направлены вниз" width="640"
у = а(х – х 0 ) 2 + у 0
Вершина параболы (х 0 ; у 0 )
Ось симметрии х = х 0
Шаблон у = a х 2
.
a 0, то ветви направлены вверх
a , то ветви направлены вниз
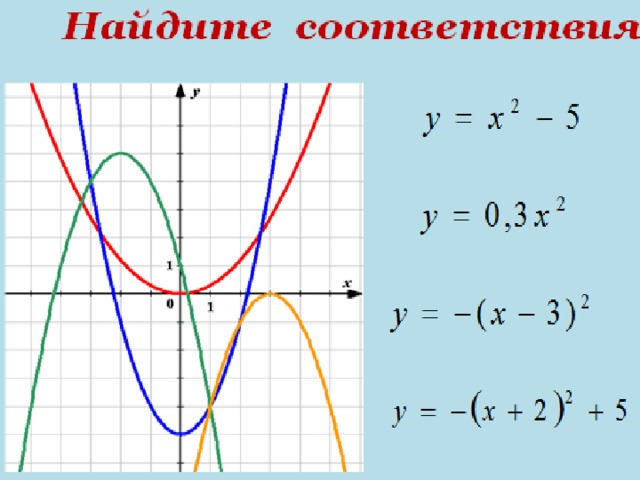


Тест проверь себя…

Проверка

Подумай…
1. Найдите координаты вершины параболы у=х 2 -4х+4
Ответ: (2;0)
- Найдите нули квадратичной функции
у=х 2 +х-2
Ответ: -2,1
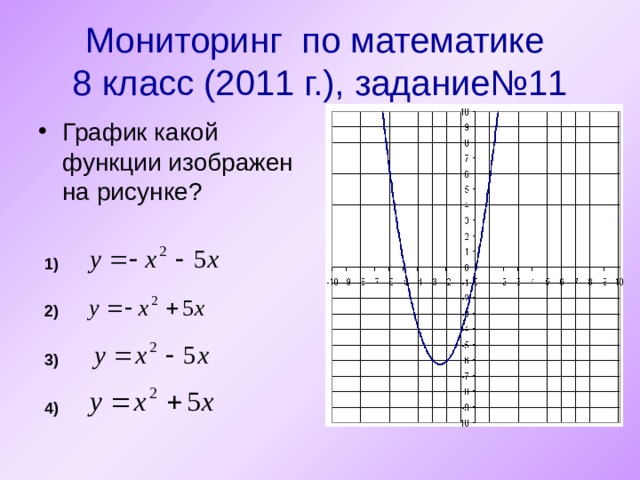
Мониторинг по математике 8 класс (2011 г.), задание№11
- График какой функции изображен на рисунке?
1)
2)
3)
4)
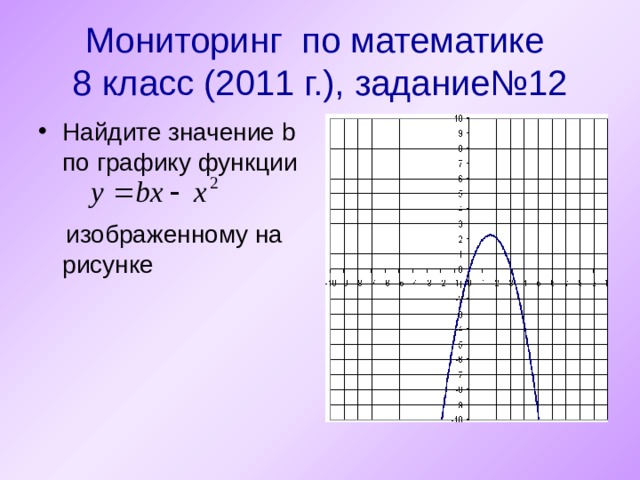
Мониторинг по математике 8 класс (2011 г.), задание№12
- Найдите значение b по графику функции
изображенному на рисунке

Построение графика функции
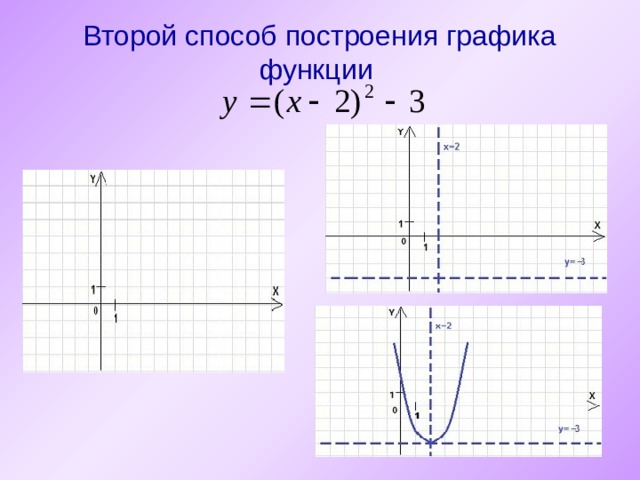
Второй способ построения графика функции
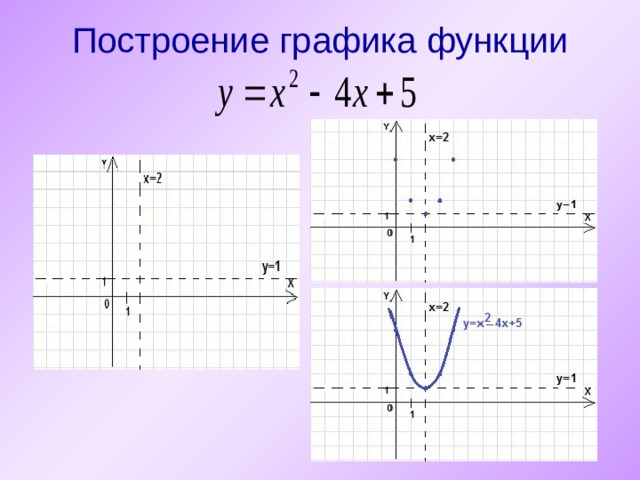
Построение графика функции

интервал для значений аргумента,
чтобы в него попала вершина
параболы;
- необходимо много считать;
- способ достаточно трудоемкий .
полный квадрат трехчлена;
находиться вершина
параболы (ось параболы).

необходим новый способ построения
графика квадратичной функции.
Этот способ должен давать возможность
быстрого и легкого нахождения координат
вершины параболы.

- находим абсциссу вершины параболы по формуле х 0 = -в / 2 а ;
- подставляя полученное значение х 0 в формулу заданной функции,
получаем у 0 ;
- построим вершину параболы с координатами ( х 0 ; у 0 );
- определим направление ветвей параболы (по коэффициенту а );
- проведем ось параболы через ее вершину;
- выбираем значения х слева или справа от оси параболы;
- вычисляем соответствующие значения у ;
- строим точки по полученным координатам и точки им симметричные
относительно оси параболы;
- соединяем точки непрерывной плавной линией.

Построить график функции

План построения
y
1) Построить вершину параболы
2) Построить ось симметрии x=-1
-1
x
-7

Проверь себя № 625(8)

Самостоятельная работа
Построить графики функций
y=x 2 + 2 x -3 y= -x 2 + 2 x + 3
План построения
- Найти вершину параболы
- Построить ось симметрии
- Найти нули функции
- Построить дополнительные точки
- Построить параболу по точкам

Проверь себя
y= x 2 + 6 x + 8 y= -x 2 + 2 x + 3
y
y
4
1
3
-1
x
-3
--1
-5
x
--1

Домашнее задание
Выучить алгоритм стр. 166,
№ 621(2,4),622 (2,4),624 (2,4),










 0 ветви параболы у = ах 2 направлены … . вверх Если а о и х 0, то функция у = ах 2 принимает … (положительные, отрицательные) значения. отрицательные" width="640"
0 ветви параболы у = ах 2 направлены … . вверх Если а о и х 0, то функция у = ах 2 принимает … (положительные, отрицательные) значения. отрицательные" width="640"
 0, то ветви направлены вверх a , то ветви направлены вниз" width="640"
0, то ветви направлены вверх a , то ветви направлены вниз" width="640"





























