Россия, Нижний Новгород
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 23.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 04.05.2025 18:58
Шустова Татьяна Венедиктовна
учитель математики
49 лет
2 128
28 743 
Местоположение
Специализация
Презентация по теме "Свойства функции"
Категория:
Алгебра
27.01.2019 21:45
Просмотр содержимого документа
«Презентация по теме "Свойства функции"»
Свойства функции.
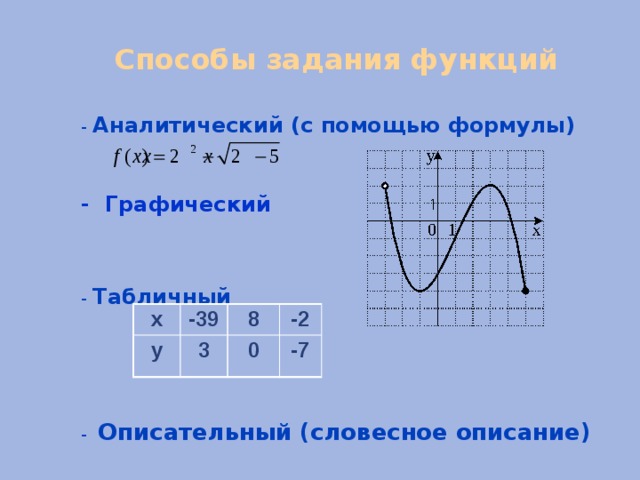
Способы задания функций
- Аналитический (с помощью формулы)
- Графический
- Табличный
- Описательный (словесное описание)
х
-39
у
8
3
-2
0
-7
Задание 1 .
Определите, какой из данных графиков является графиком функции
Рис.1 Рис.2 Рис.3 Рис.4
у
у
у
у
х
х
х
х
НЕ ЯВЛЯЮТСЯ графиками функций рис.1, рис. 3,рис. 4
Свойства функции
1.Область определения функции
– все значения, которые принимает независимая переменная (х).
Обозначается : D (f).
2. Область значений функции
– все значения, которые принимает зависимая переменная (у).
Обозначается : E (f)
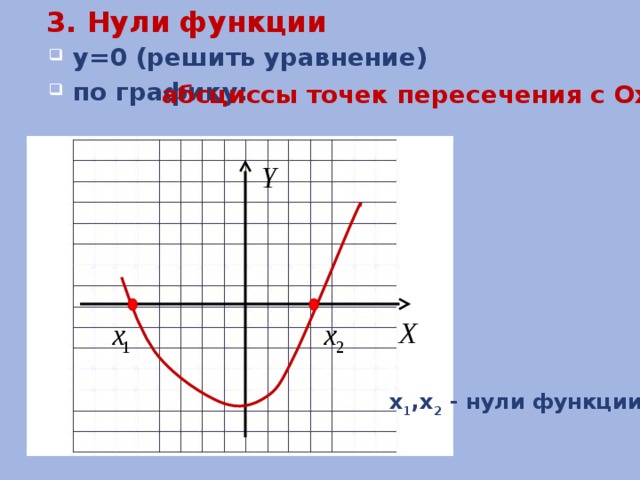
3. Нули функции
- у=0 (решить уравнение)
- по графику:
абсциссы точек пересечения с Ох
x 1 ,x 2 - нули функции
0, y по графику: выше/ниже оси Ох " width="640"
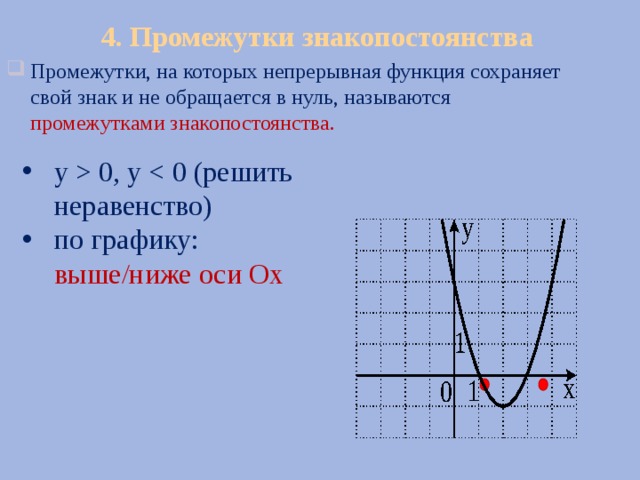
4. Промежутки знакопостоянства
- Промежутки, на которых непрерывная функция сохраняет свой знак и не обращается в нуль, называются промежутками знакопостоянства.
- y 0, y
- по графику: выше/ниже оси Ох
f(х 2 ) . Функцию у = f(х) называют возрастающей на множестве Х , если для любых двух точек х 1 и х 2 из области определения, таких, что х 1 2 , выполняется неравенство f(х 1 ) 2 ) . по графику: f(x 2 ) f(x 1 ) f(x 2 ) x 1 x 2 x 1 x 2 f(x 1 ) x 2 х 1 " width="640"
5. Монотонность (возрастание, убывание)
Функцию у = f(х) называют убывающей на множестве Х , если для любых двух точек
х 1 и х 2 из области определения, таких, что х 1 2 , выполняется неравенство
f(х 1 ) f(х 2 ) .
Функцию у = f(х) называют возрастающей на множестве Х , если для любых двух точек х 1 и х 2 из области определения, таких, что х 1 2 , выполняется неравенство
f(х 1 ) 2 ) .
- по графику:
f(x 2 )
f(x 1 )
f(x 2 )
x 1
x 2
x 1
x 2
f(x 1 )
x 2
х 1
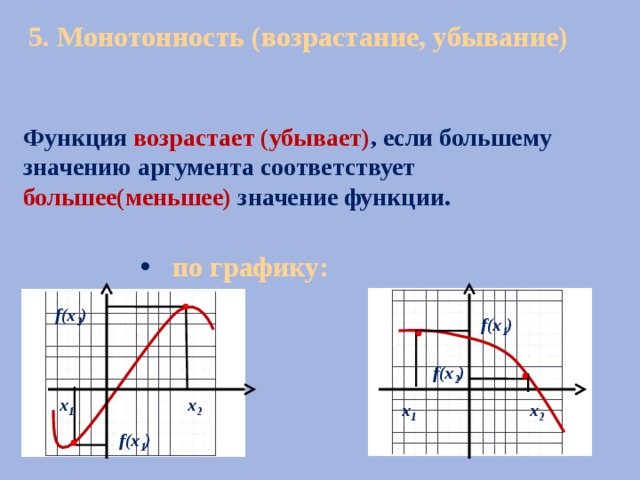
5. Монотонность (возрастание, убывание)
Функция возрастает (убывает) , если большему значению аргумента соответствует большее(меньшее) значение функции.
- по графику:
f(x 2 )
f(x 1 )
f(x 2 )
x 2
x 1
x 2
x 1
f(x 1 )
х 1
x 2
Примеры.
- у=5-2х
- у= - , х
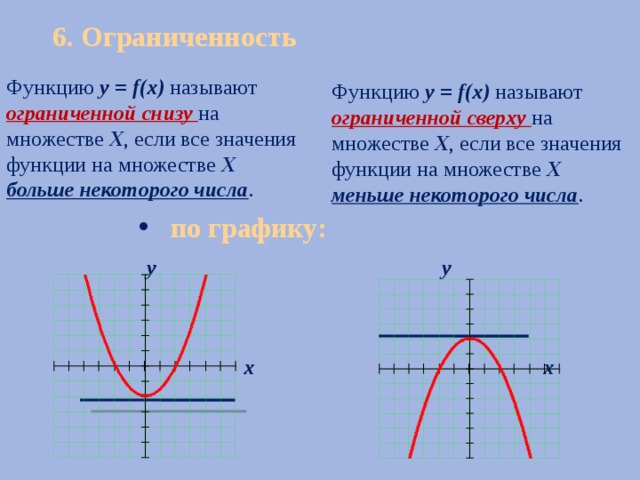
6. Ограниченность
Функцию у = f(х) называют ограниченной снизу на множестве Х , если все значения функции на множестве Х больше некоторого числа .
Функцию у = f(х) называют ограниченной сверху на множестве Х , если все значения функции на множестве Х меньше некоторого числа .
- по графику:
у
у
х
х
0 у= х 2 -4х+1, х у= " width="640"
Примеры.
- у=4х+1, х0
- у= х 2 -4х+1, х
- у=
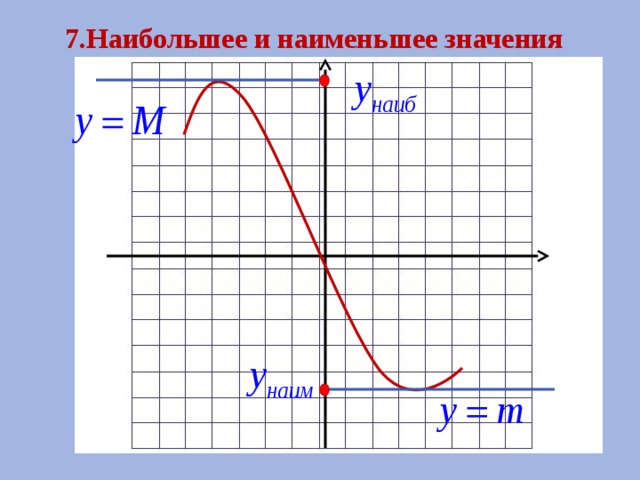
7.Наибольшее и наименьшее значения
7.Наибольшее и наименьшее значения
Число m называют наименьшим значением функции
у = f(х) на множестве Х , если:
1) в области определения существует такая точка х 0 , что f(х 0 ) = m .
2) всех х из области определения выполняется неравенство
f(х) ≥ f(х 0 ).
Число M называют наибольшим значением функции
у = f(х) на множестве Х , если:
1) в области определения существует такая точка х 0 , что f(х 0 ) = M .
2) для всех х из области определения выполняется неравенство
f(х) ≤ f(х 0 ).
![Примеры. у=2х+3, х Є [0;1] у=](https://fsd.multiurok.ru/html/2019/01/27/s_5c4dfbae7ee98/img13.jpg)
Примеры.
- у=2х+3, х Є [0;1]
- у=
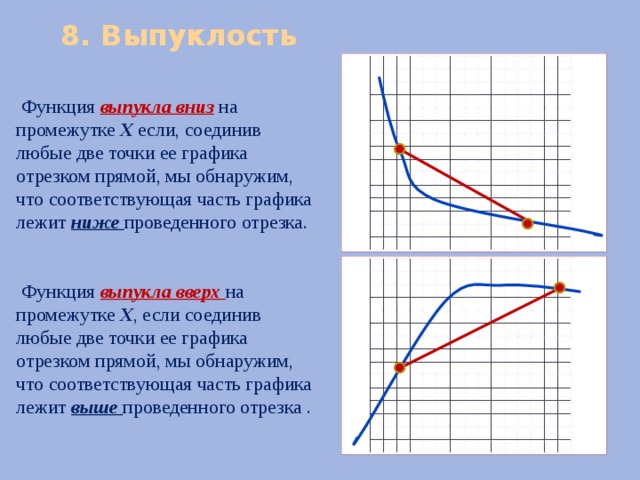
8. Выпуклость
Функция выпукла вниз на промежутке Х если, соединив любые две точки ее графика отрезком прямой, мы обнаружим, что соответствующая часть графика лежит ниже проведенного отрезка.
Функция выпукла вверх на промежутке Х , если соединив любые две точки ее графика отрезком прямой, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка .
9. Непрерывность
Функция называется непрерывной на промежутке, если она определена на этом промежутке и непрерывна в каждой точке этого промежутка.
Непрерывность функции на промежутке Х означает, что график функции на всей области определения сплошной, т.е. не имеет проколов и скачков.
Задание . Определите, на каком из рисунков изображен график непрерывной функции .
подумай
правильно
1
2
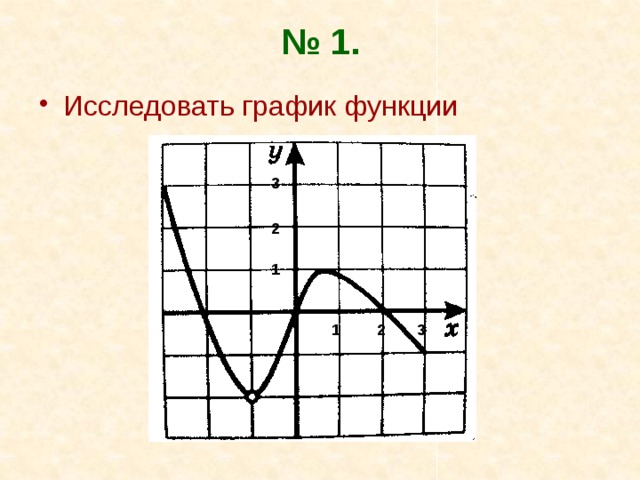
№ 1.
- Исследовать график функции
3
2
1
1
2
3
Решение упражнений.
№ 10.14, 10.17, 10.23а
Домашнее задание.
§ 10, № 10.15, 10.16, 10.23г
10. Четность
Нечетная функция
Четная функция
Функция y = f(x) называется нечетной , если для любого хЄХ выполняется равенство
f (-x) = - f (x) .
Функция y = f(x) называется четной , если для любого хЄХ выполняется равенство
f (-x) = f (x).
Примеры.
- у=3х 2 +х 4
- у=
- у=3х-4
если х Є Х, то -х Є Х
Х- симметричное множество
4) у=
8
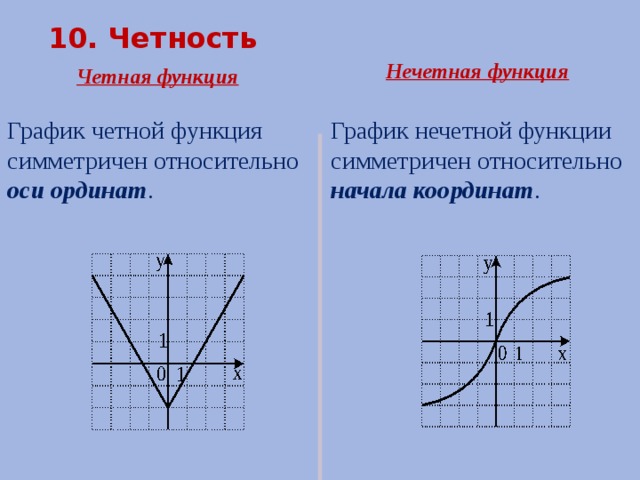
10. Четность
Нечетная функция
Четная функция
График четной функция симметричен относительно оси ординат .
График нечетной функции симметричен относительно начала координат .
8
Решение упражнений.
№ 11.1-2(у), 11.7(аб),11.8(аб),
11.9-10(у), 11.11(аб)
Домашнее задание.
§ 10-11, № 11.3,4,7,11,21 (все – вг)
© 2019, Шустова Татьяна Венедиктовна 1286 21
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
