Презентация "Аксиомы стереометрии"

«Основные понятия и

аксиомы стереометрии,

следствия из аксиом ».

Работу подготовила ученица 9-Б класса Валерия Мильгевская МОШ/-/// ст. №53

Простейшие фигуры стереометрии .

 С

точка С

В 

А  прямая АВ

n прямая n

А 

В  С 

плоскость АВС

плоскость 

α

Основные обозначения:

А  Ф –точка А принадлежит фигуре Ф;

А  Ф – точка А не принадлежит фигуре Ф;

Ф 1  Ф – фигура Ф 1 является подмножеством фигуры Ф;

Ф 1  Ф – фигура Ф 1 не является подмножеством фигуры Ф;

Ф 1  Ф 2 – пересечение фигур Ф 1 и Ф 2 ;

 - следовательно

Аксиомы стереометрии.

А 1. Через три точки, не лежащие на одной прямой,

проходит плоскость, и притом только одна.

 D  N

D  α

 S

N  α

α

S  α  α- единственная

D  NS

А 2. Если две точки прямой лежат в плоскости,

то все точки прямой лежат в этой плоскости .

• D

• C

• N

N  α

D  α  C  α

С  ND

т. е. прямая ND  α

α

β

А 3 . Если две плоскости имеют общую точку,

то они имеют общую прямую, на которой

лежат все общие точки этих плоскостей.

α

А

В

А  α

 α  β = АВ

А  β

Следствия из аксиом.

Т 1 Через прямую и не лежащую на ней точку

проходит плоскость, и притом только одна.

а

А

α

А  α

А  а  α- единственная

а  α

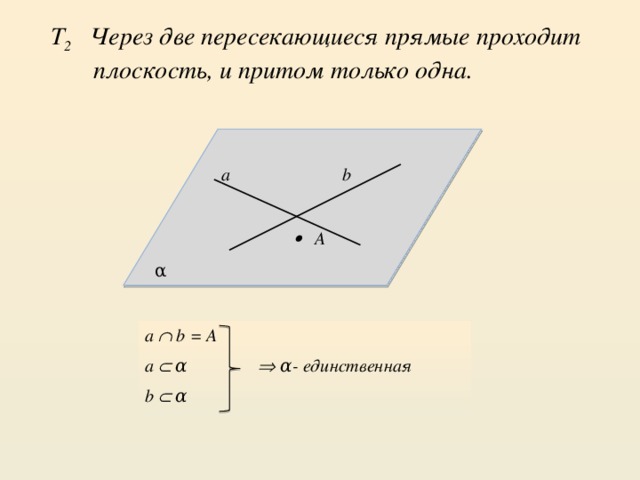
Т 2 Через две пересекающиеся прямые проходит

плоскость, и притом только одна.

а b

 А

α

а  b = А

а  α  α- единственная

b  α