Разработка урока № 1 "Упрощение выражений" (5 класс, учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков и др.)

У р о к № 1. Упрощение выражений

Основная дидактическая цель урока: познакомить учащихся с распределительным свойством умножения относительно сложения и относительно вычитания, учить применять это свойство при устных вычислениях.

Х о д у р о к а

I. Организационный момент

II. Устный счёт

Математическое лото.

– Закройте соответствующие клеточки. Из оставшихся букв сложите слово.

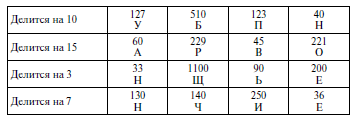
Ответ: Упрощение.

III. Работа по теме урока

Тема нашего сегодняшнего урока «Упрощение выражений».

– Повторим законы сложения и умножения.

Переместительные законы:

а + b = b + a

a ・ b = b ・ a

Сочетательные свойства:

(a + b) + c = a + (b + c)

a ・ (b ・ c) = (a ・ b) ・ c

Распределительный закон:

(a + b) ・ c = ac + bc

(а - b) ・ c = ac - bc

– Для чего мы изучаем эти свойства? (С помощью свойств легче, быстрее, удобнее считать.)

IV. Работа по учебнику

1. С. 98–99 (работа по статье учебника).

– Прочитайте статью учебника и приготовьтесь отвечать на вопросы.

– Сформулируйте распределительное свойство умножения относительно сложения.

– Сформулируйте свойство умножения относительно вычитания.

– Объясните, для чего мы изучаем распределительное свойство умножения.

– Запишите распределительное свойство умножения относительно сложения и относительно вычитания при помощи букв.

2. На столе стоят три вазы с сиренью. В первой вазе х веток сирени, во второй – в 2 раза больше, а в третьей – в 3 раза больше, чем в первой. Сколько веток сирени во второй и третьей вазах?

Первая ваза – х.

Вторая ваза – 2 ・ х.

Третья ваза – 3 ・ х.

Всего во второй и третьей вазах – 2 ・ х + 3 ・ х.

Преобразуем выражение, применяя распределительное свойство умножения

2 ・ х + 3 ・ х = х ・ (2 + 3) = х ・ 5 = 5х.

Итак, распределительное свойство умножения позволяет упрощать буквенные выражения

3а + 7а = а(3 + 7) = 10а

27у - 12у = у(27 - 12) = 15у

49х + х = х(49 + 1) = 50х

63b - b = b(63 - 1) = 62b.

Таким образом, данные выражения мы записали в более простом виде, или, как говорят математики, упростили. Такие преобразования, в результате которых получаются более простые выражения, называют упрощением выражений.

Рассмотрим выражение 3у. Это произведение числа 3 и буквы у. Говорят, что число 3 – числовой множитель, а буква у – буквенный множитель. Числовой множитель обычно в таких выражениях называют коэффициентом.

Упрощая выражения, мы складывали коэффициенты, а буквенный множитель мы оставляли без изменения. Обычно промежуточные записи не делают, а пишут так:

8у - 3у = 5у; 17х + х = 18х.

Мы рассмотрели буквенные выражения, у которых одинаковая буквенная часть. Такие выражения называют подобными.

А выражение 27х + 7у упростить нельзя, потому что их буквенные части разные.

Отметим, что распределительный закон умножения верен не только для двух, а для любого числа слагаемых.

3. Упростите выражение.

2(а + 6) + 3(а + 2) = 2а + 12 + 3а + 6 = 5а + 18

3(а + 2b + 4) + 7(2a + 4b + 1) = 3a + 6b + 12 + 14a + 28b + 7 = 17a + 34b + 19

4. Укажите, какой способ решения проще.

1) (100 + 30) ・ 8 = 130 ・ 8 = 1040 или

(100 + 30) ・ 8 = 100 ・ 8 + 30 ・ 8 = 1040

2) (200 - 1) ・ 7 = 199 ・ 7 = 1393 или

200 ・ 7 - 1 ・ 7 = 1393

5. С. 100, № 3.192.

– Прочитайте задание.

Распределительное свойство умножения нужно уметь видеть и узнавать и по второй части записи.

(a + b) ・ c = a ・ c + b ・ c

47 ・ 34 + 53 ・ 34

– Какой множитель повторяется?

– Какой знак стоит между произведениями?

– Как «собрать» запись?

(Далее задание выполняется в паре.)

(3440, 8700, 54 000, 7200, 18 000, 80 100.)

V. Работа над задачей

С. 100, № 3.182.

– Прочитайте задачу.

– О чём говорится в задаче?

– Сколько купили глубоких тарелок?

– Сколько купили мелких тарелок?

– Какая стоимость глубоких тарелок?

– Какая стоимость мелких тарелок?

– Можно ли узнать стоимость всех тарелок?

– Запишите решение выражением.

(12 ・ (190 + 160) = 4200 (р).)

– Можно ли решить задачу иначе?

– Запишите выражение.

(190 ・ 12 + 160 ・ 12 = 4200 (р).)

– Сравните два способа решения.

– Что вы заметили?

VI. Повторение изученного материала

С. 104, № 3.245 (работа в паре с последующей взаимопроверкой).

(104, 2500, 26 000, 11.)

VII. Рефлексия

– Какое новое знание вы получили на уроке?

– Сформулируйте распределительное свойство умножения относительно сложения, относительно вычитания.

Домашнее задание

С. 104, № 3.248; с. 105, № 3.253.