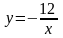Диагностическая работа №2 (октябрь). Модуль «Алгебра».
Вариант -1.
11.1 Установите соответствие между графиками и формулами
А. 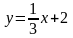 Б.
Б. 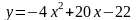 В.
В. 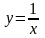
1) 2)
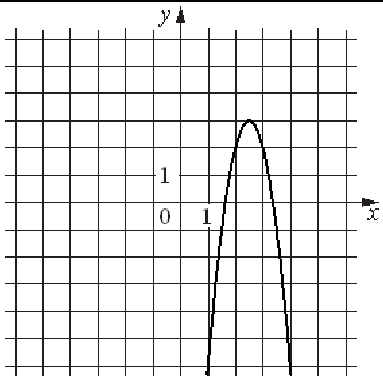
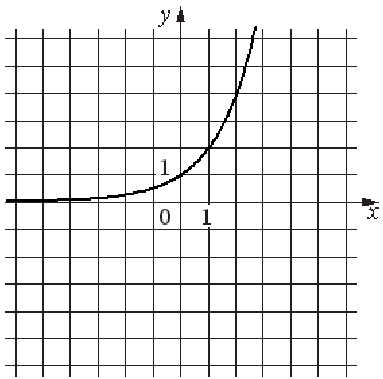
3) 4)
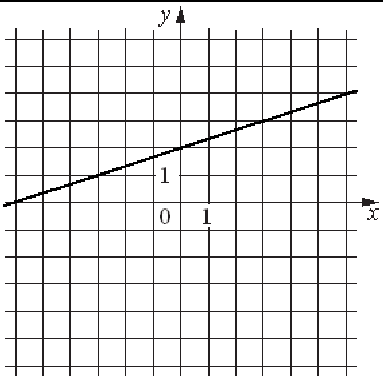
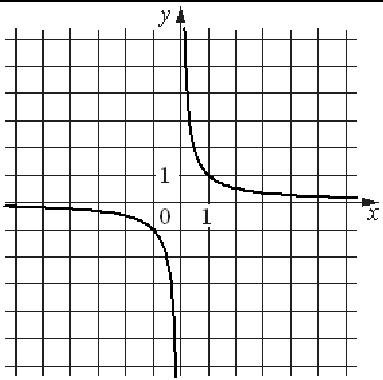
Заполните таблицу
11.2 Найти область определения функции 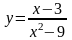
11.3 Найти область определения функции 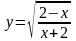
11.4 Вычислите координаты точки пересечения параболы 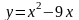 и прямой
и прямой 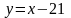 .
.
11. 5
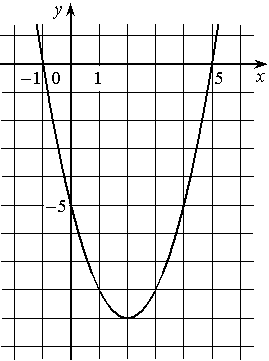
На рисунке изображен график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Наименьшее значение функции равно -5.
2) Функция убывает на промежутке 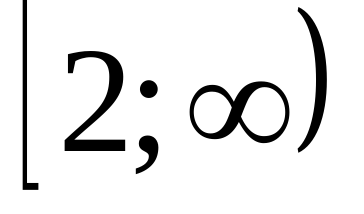
3) 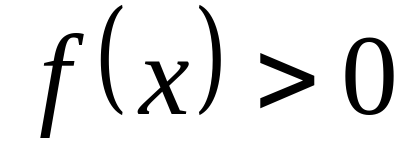 при
при 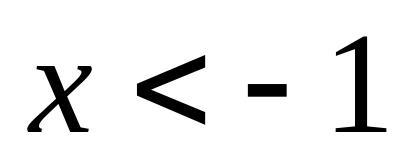 и при
и при 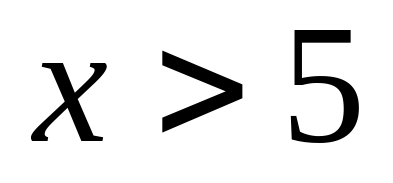
Часть 2.
20.1 Решите неравенство 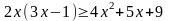
22.1 Постройте график функции 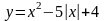 и найдите все значения а, при которых прямая у = а имеет с графиком данной функции ровно три общие точки.
и найдите все значения а, при которых прямая у = а имеет с графиком данной функции ровно три общие точки.
Диагностическая работа №2 (октябрь). Модуль «Алгебра».
Вариант -2.
11.1 Установите соответствие между графиками и формулами
А. 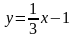 Б.
Б. 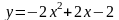 В.
В. 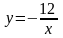
1) 2)
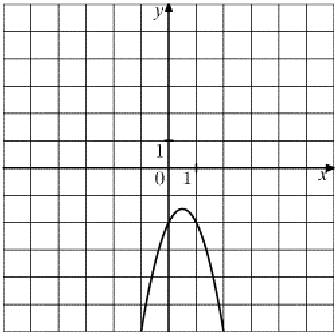
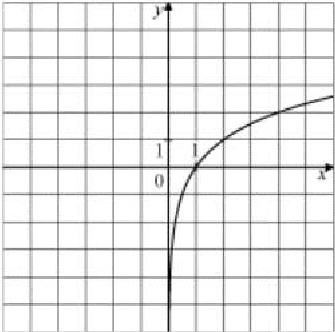
3) 4)
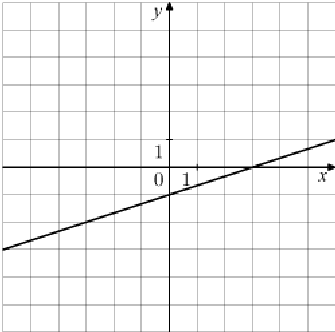
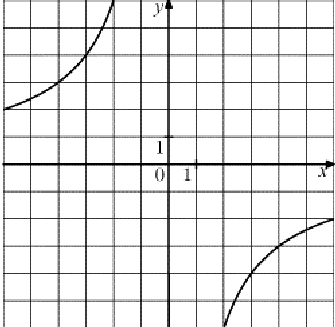
Заполните таблицу
11.2 Найти область определения функции 
11.3 Найти область определения функции 
11.4 Вычислите координаты точки пересечения параболы  и прямой
и прямой  .
.
11. 5
На рисунке изображен график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Наименьшее значение функции равно 2,5.
2) Функция убывает на промежутке 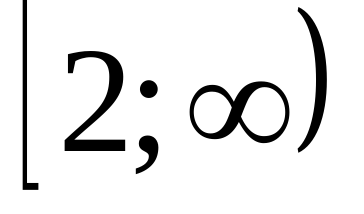
3) 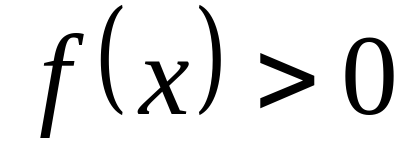 при
при 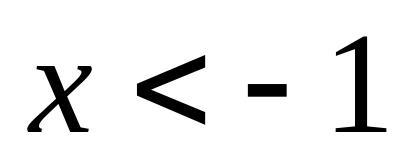 и при
и при 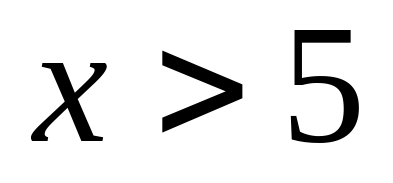
Часть 2.
20.1 Решите неравенство
22.1 Постройте график функции  и найдите все значения а, при которых прямая у = а имеет с графиком данной функции ровно три общие точки.
и найдите все значения а, при которых прямая у = а имеет с графиком данной функции ровно три общие точки.
Диагностическая работа №2 (октябрь). Модуль «Алгебра».
Вариант -3.
11.1 Установите соответствие между графиками и формулами
А.  Б.
Б.  В.
В. 
1) 2)
3) 4)
Заполните таблицу
11.2 Найти область определения функции 
11.3 Найти область определения функции 
11.4 Вычислите координаты точки пересечения параболы  и прямой
и прямой  .
.
11. 5
На рисунке изображен график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Наименьшее значение функции равно 10.
2) Функция возрастает на промежутке 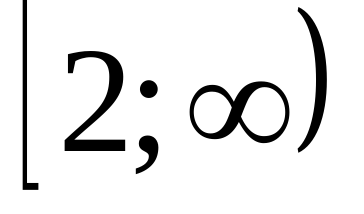
3)  при
при 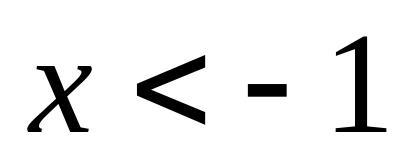 и при
и при 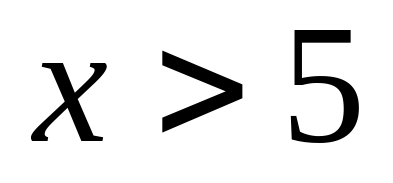

Часть 2.
20.1 Решите неравенство
22.1 Постройте график функции  и найдите все значения а, при которых прямая у = а имеет с графиком данной функции ровно одну общую точку.
и найдите все значения а, при которых прямая у = а имеет с графиком данной функции ровно одну общую точку.





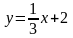 Б.
Б. 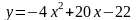 В.
В. 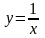




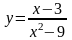
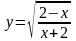
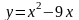 и прямой
и прямой 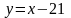 .
.
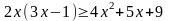
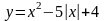 и найдите все значения а, при которых прямая у = а имеет с графиком данной функции ровно три общие точки.
и найдите все значения а, при которых прямая у = а имеет с графиком данной функции ровно три общие точки.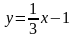 Б.
Б. 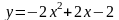 В.
В.