Двугранный угол.

Урок геометрии, 10 класс

Тема: «Двугранный угол».

Цель урока: ввести понятия двугранного угла и его линейного угла, рассмотреть задачи на применение этих понятий, сформировать навыки нахождения угла между плоскостями.

Задачи:

Обучающая: формирование способности запоминания основной терминологии, формирование навыков правильного оформления записей.

Воспитательная: дисциплинированность, уверенность в себе, уважительное отношение к окружающим, аккуратность, самостоятельность, трудолюбие, точность.

Развивающая: развитие математической речи, логического мышления, внимания, сообразительности, ответственности, привитие интереса к предмету.

Материалы и оборудование: компьютер, проектор, линейка, цветной мел.

Тип урока: урок изучения нового материала

Этапы урока:

1. Организационный (приветствие, объявление темы и цели урока, проверка готовности к уроку).

2. Актуализация опорных знаний.

1. Проверка домашнего задания. Проверяем № 159.

2. Определение угла на плоскости.

3. Определение угла между двумя пересекающимися прямыми в пространстве.

4. Определение угла между двумя скрещивающимися прямыми в пространстве.

5. Определение угла между прямой и плоскостью.

1. Объяснение нового материала.

Познакомимся с еще одним видом углов – двугранным углом.

Чтобы ввести понятие двугранного угла, следует напомнить, что любая прямая, проведенная в данной плоскости, разделяет эту плоскость на две полуплоскости (рис.1,а)

а) б)

Рис. 1

Представим себе, что мы перегнули плоскость по прямой так, что две полуплоскости с границей оказались уже не лежащими в одной плоскости , как показано на рис. 1, б. Полученная фигура и есть двугранный угол.

Определение. Двугранным углом называется фигура, образованная прямой и двумя полуплоскостями с общей границей, не принадлежащими одной плоскости. Полуплоскости, образующие двугранный угол, называются его гранями. У двугранного угла две грани, отсюда и название — двугранный угол. Прямая — общая граница полуплоскостей — называется ребром двугранного угла.

Вопрос к учащимся: Приведите примеры из обыденной жизни предметов и конструкций, имеющих форму двугранного угла..

Полураскрытая папка, стена комнаты совместно с полом, двускатные крыши зданий.

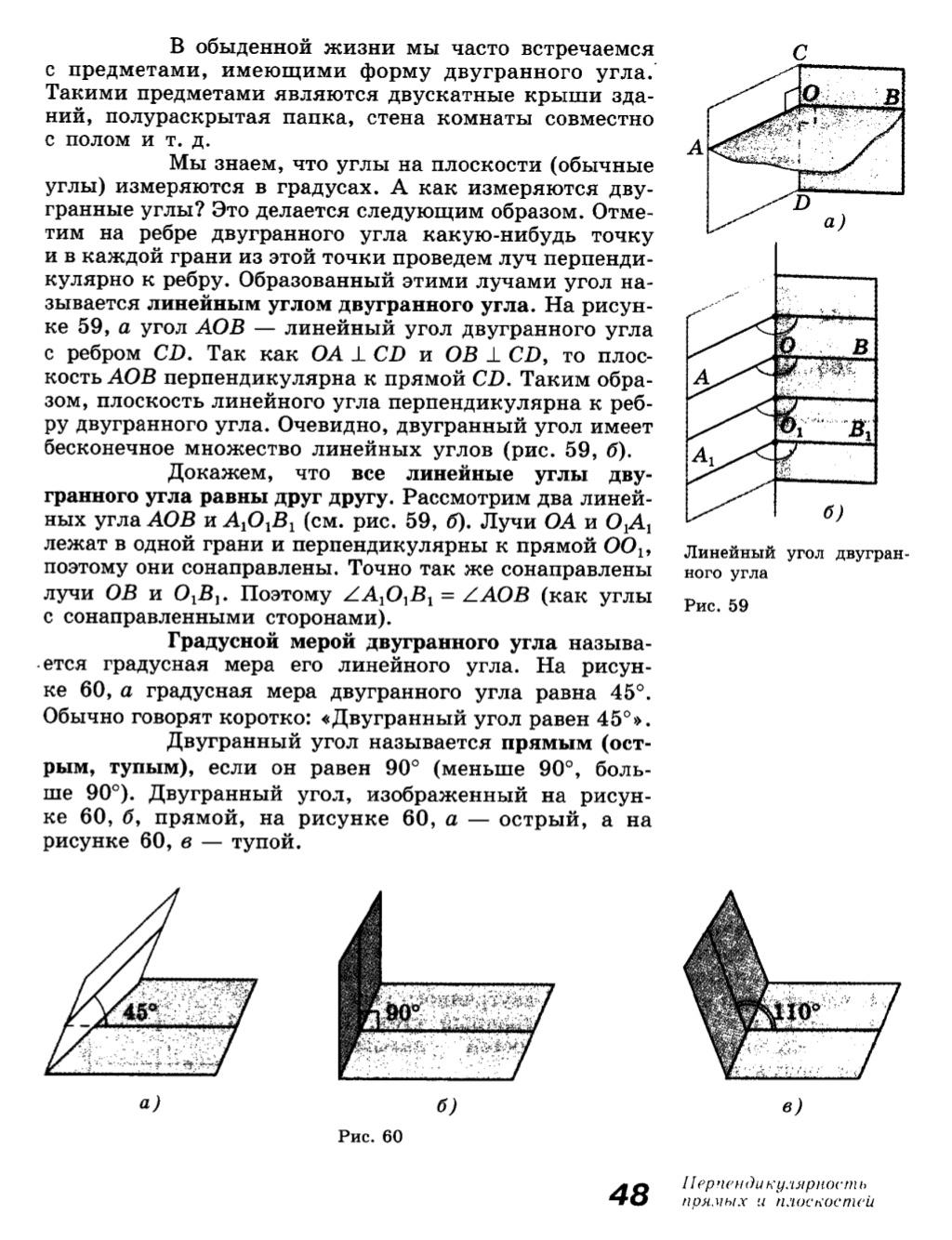
Как известно, углы на плоскости измеряются в градусах. Чтобы измерить двугранный угол, поступим следующим образом. Отметим на ребре двугранного угла какую-нибудь точку и в каждой грани из этой точки проведем луч перпендикулярно к ребру. Образованный этими лучами угол называется линейным углом двугранного угла. Сделайте чертёж у себя в тетрадях.

О ∈ а, АО ⊥ а, ВО ⊥ a, САBD – двугранный угол, ∠AOB – линейный угол двугранного угла.

С

А ЩО В

D Рис. 2

Все линейные углы двугранного угла равны. Сделаем рисунок.

А О В

Р Q R

Рис. 3

Доказательство. Рассмотрим два линейных угла АОВ и PQR. Лучи ОА и QP лежат в одной грани и перпендикулярны OQ, значит, они сонаправлены. Аналогично лучи ОВ и QR сонаправлены. Значит, ∠AOB = ∠PQR (как углы с сонаправленными сторонами).

Градусной мерой двугранного угла называется градусная мера его линейного угла. Перерисуйте из учебника со страницы 48 изображения острого, прямого и тупого двугранного угла.

1. Закрепление изученного материала.

Выполним несколько заданий.

№ 1. Дано: ΔABC, АС = ВС, АВ лежит в плоскости α, CD ⊥ α, С ∉ α. Построить линейный угол двугранного угла CABD.

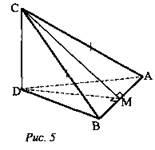
Решение.  CM ⊥ AB, DC ⊥ АВ. ∠CMD - искомый.

№ 2. Дано: ΔABC, ∠C = 90°, ВС лежит плоскости α, АО ⊥ α, A ∈ α.

Построить линейный угол двугранного угла АВСО.

Решение. AB ⊥ BC, АО ⊥ ВС, значит, ОС ⊥ ВС. ∠ACO - искомый.

№ 3. Дано: ΔABC, ∠С = 90°, АВ лежит в плоскости α, CD ⊥ α, С ∉ α. Построить линейный угол двугранного угла DABC.

Решение.  CK ⊥ AB, DC ⊥ АВ, DK ⊥ АВ, значит, ∠DKC - искомый.

№ 4. Дано: DABC - тетраэдр, DO ⊥ ABC. Построить линейный угол двугранного угла  ABCD.

Решение.  DM ⊥ ВС, DO ⊥ ВС, значит, ОМ ⊥ ВС; ∠OMD -  искомый.

1. Домашнее задание. п. 22, №167, №170.

2. Итог урока.

Что нового вы узнали сегодня на уроке? Какова была цель нашего урока? Достигнута ли она?