РЕШУ ЕГЭ — математика профильная
Вариант № 79337494
1.
i
 В треугольнике ABC угол C равен 90°,
В треугольнике ABC угол C равен 90°, 
 Найдите высоту CH.
Найдите высоту CH.
2.
i
Даны векторы 
 и
и  Найдите сумму координат вектора
Найдите сумму координат вектора 
3.
i
 Объем первого куба в 8 раз больше объема второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Объем первого куба в 8 раз больше объема второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
4.
i
В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете не будет вопроса о грибах.
5.
i
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
6.
i
Найдите корень уравнения 
7.
i
Найдите значение выражения  если
если 
8.
i
На рисунке изображен график функции  и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку. 
9.
i
Высота над землeй подброшенного вверх мяча меняется по закону  где h − высота в метрах, t − время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?
где h − высота в метрах, t − время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?
10.
i
Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.
11.
i
 На рисунке изображён график функции
На рисунке изображён график функции  Найдите a.
Найдите a.
12.
i
Найдите наименьшее значение функции  на отрезке
на отрезке 
13.
i
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие промежутку 
14.
i
В правильной треугольной призме ABCA1B1C1 известны рёбра: AB AA1 = 4. Точка M — середина ребра BC.
AA1 = 4. Точка M — середина ребра BC.
а) Докажите, что прямые B1C и C1M перпендикулярны.
б) Найдите угол между прямой C1M и плоскостью грани ABB1A1.
15.
i
Решите неравенство 
16.
i
1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита следующая: 1 марта каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем второй платеж оказался в два раза больше первого, а третий – в три раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2 395 800 рублей?
17.
i
В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке M , причём AM = 2R и CM = 3R.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите расстояние между центрами его вписанной и описанной окружностей, если известно, что R = 2 .
18.
i
При каких значениях параметра а система  имеет четыре решения?
имеет четыре решения?
19.
i
На окружности некоторым способом расставили натуральные числа от 1 до 21 (каждое число поставлено по одному разу). Затем для каждой пары соседних чисел нашли разность большего и меньшего.
а) Могли ли все полученные разности быть не меньше 11?
б) Могли ли все полученные разности быть не меньше 10?
в) Помимо полученных разностей, для каждой пары чисел, стояших через одно, нашли разность большего и меньшего. Для какого наибольшего целого числа k можно так расставить числа, чтобы все разности были не меньше k?







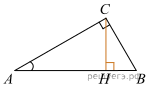 В треугольнике ABC угол C равен 90°,
В треугольнике ABC угол C равен 90°,  Объем первого куба в 8 раз больше объема второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Объем первого куба в 8 раз больше объема второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?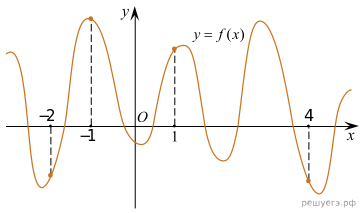
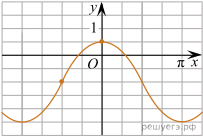 На рисунке изображён график функции
На рисунке изображён график функции 


















