РЕШУ ЕГЭ — математика профильная
Вариант № 79337496
1. Тип 1 № 27925 
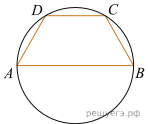 Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
2. Тип 2 № 644820 
 На координатной плоскости изображены векторы
На координатной плоскости изображены векторы 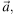
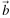 и
и 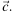 Вектор
Вектор 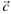 разложен по двум неколлинеарным векторам
разложен по двум неколлинеарным векторам  и
и 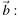
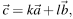
где k и l — коэффициенты разложения. Найдите k.
3. Тип 3 № 245355 
 Куб вписан в шар радиуса
Куб вписан в шар радиуса 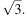 Найдите объем куба.
Найдите объем куба.
4. Тип 4 № 320192 
В классе 26 учащихся, среди них два друга — Андрей и Сергей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
5. Тип 5 № 621772 
В коробке 8 синих, 6 красных и 11 зелёных фломастеров. Случайным образом выбирают два фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
6. Тип 6 № 26658 
Найдите корень уравнения 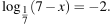
7. Тип 7 № 26744 
Найдите значение выражения 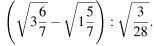
8. Тип 8 № 119971 
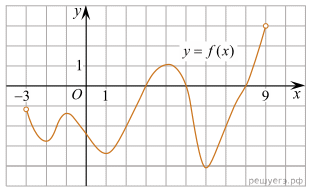 На рисунке изображен график функции y = f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых производная функции f(x) равна 0.
На рисунке изображен график функции y = f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых производная функции f(x) равна 0.
9. Тип 9 № 27986 
Расстояние (в км) от наблюдателя, находящегося на высоте h м над землeй, до видимой им линии горизонта вычисляется по формуле 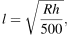 где
где 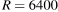 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?
км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?
10. Тип 10 № 99578 
Имеются два сосуда. Первый содержит 30 кг, а второй − 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
11. Тип 11 № 509229 
 На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
12. Тип 12 № 245176 
Найдите наибольшее значение функции 
13. Тип 13 № 501507 
а) Решите уравнение 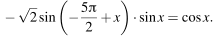
б) Найдите все корни этого уравнения, принадлежащие отрезку 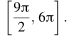
14. Тип 14 № 505566 
В конус, радиус основания которого равен 3, вписан шар радиуса 1,5.
а) Изобразите осевое сечение комбинации этих тел.
б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.
15. Тип 15 № 484586 
Решите неравенство 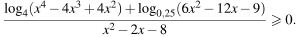
16. Тип 16 № 516053 
Пенсионный фонд владеет акциями, цена которых к концу года t становится равной t2 тыс. руб. (т. е. к концу первого года они стоят 1 тыс. руб., к концу второго — 4 тыс. руб. и т. д.), в течение 20 лет. В конце любого года можно продать акции по их рыночной цене на конец года и положить вырученные деньги в банк под 25% годовых. В конце какого года нужно продать акции, чтобы прибыль была максимальной?
17. Тип 17 № 514508 
Точки A1, B1 и C1 — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.
а) Докажите, что отличная от A1 точка пересечения окружностей, описанных около треугольников A1CB1 и A1BC1, лежит на окружности, описанной около треугольника B1AC1.
б) Известно, что AB = AC = 10 и BC = 12. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры окружностей, описанных около треугольников A1CB1, A1BC1 и B1AC1.
18. Тип 18 № 484633 
При каких значениях параметров а и b система 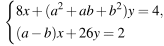 имеет бесконечно много решений?
имеет бесконечно много решений?
19. Тип 19 № 517572 
На доске написано 30 натуральных чисел. Какие-то из них красные, а какие-то зелёные. Красные числа кратны 7, а зелёные числа кратны 5. Все красные числа отличаются друг от друга, как и все зелёные. Но между красными и зелёными могут быть одинаковые.
а) Может ли сумма всех чисел, записанных на доске, быть меньше 2325, если на доске написаны только кратные 5 числа?
б) Может ли сумма чисел быть 1467, если только одно число красное?
в) Найдите наименьшее количество красных чисел, которое может быть при сумме 1467.








 Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции. На координатной плоскости изображены векторы
На координатной плоскости изображены векторы  Куб вписан в шар радиуса
Куб вписан в шар радиуса 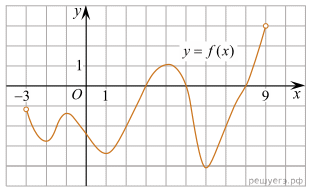 На рисунке изображен график функции y = f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых производная функции f(x) равна 0.
На рисунке изображен график функции y = f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых производная функции f(x) равна 0. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.



















