РЕШУ ЕГЭ — математика профильная
Вариант № 79337489
1.
i
 В треугольнике ABC угол C равен 90°,
В треугольнике ABC угол C равен 90°, 
 Найдите
Найдите 
2.
i
 Найдите квадрат длины вектора
Найдите квадрат длины вектора  +
+ 
3.
i
 Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
4.
i
Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
5.
i
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
6.
i
Решите уравнение  Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
7.
i
Найдите значение выражения  если
если 
8.
i
На рисунке изображён график некоторой функции y = f(x). Функция  — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
9.
i
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием  см. Расстояние
см. Расстояние  от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние
от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние  от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение
от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение  Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
10.
i
Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20 000 рублей, через два года был продан за 15 842 рублей.
11.
i
 На рисунке изображён график функции
На рисунке изображён график функции  Найдите значение x, при котором
Найдите значение x, при котором 
12.
i
Найдите наименьшее значение функции  на отрезке
на отрезке 
13.
i
а) Решите уравнение: 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
14.
i
В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 4, точка N — середина ребра AC, точка O центр основания пирамиды, точка P делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.
а) Докажите, что прямая NP перпендикулярна прямой BS.
б) Найдите расстояние от точки B до прямой NP.
15.
i
Решите неравенство: 
16.
i
В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у. е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
17.
i
Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC, перпендикулярна CM и пересекает катет AC в точке K. При этом AK : KC = 1 : 2.
а) Докажите, что 
б) Пусть прямые MK и BC пресекаются в точке P, а прямые AP и BK — в точке Q. Найдите KQ, если BC = 
18.
i
При каких значениях параметра a уравнение

имеет ровно 2 различных решения.
19.
i
Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более  от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более
от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более  от общего числа учащихся группы, посетивших кино.
от общего числа учащихся группы, посетивших кино.
а) Могло ли быть в группе 10 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?
б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?
в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а) и б)?
Просмотр содержимого документа
«ЕГЭ 2024 Декабрь Математика Вариант 5»
РЕШУ ЕГЭ — математика профильная
Вариант № 79337489
1.
i
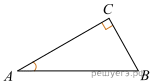 В треугольнике ABC угол C равен 90°,
В треугольнике ABC угол C равен 90°, 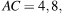
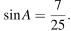 Найдите
Найдите 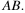
2.
i
 Найдите квадрат длины вектора
Найдите квадрат длины вектора 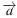 +
+ 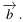
3.
i
 Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
4.
i
Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
5.
i
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
6.
i
Решите уравнение 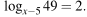 Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
7.
i
Найдите значение выражения  если
если 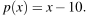
8.
i
На рисунке изображён график некоторой функции y = f(x). Функция 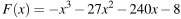 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
9.
i
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием 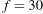 см. Расстояние
см. Расстояние  от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние
от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние 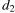 от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение
от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение 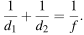 Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
10.
i
Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20 000 рублей, через два года был продан за 15 842 рублей.
11.
i
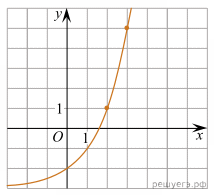 На рисунке изображён график функции
На рисунке изображён график функции 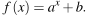 Найдите значение x, при котором
Найдите значение x, при котором 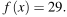
12.
i
Найдите наименьшее значение функции 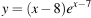 на отрезке
на отрезке 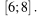
13.
i
а) Решите уравнение: 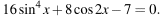
б) Найдите все корни этого уравнения, принадлежащие отрезку 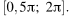
14.
i
В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 4, точка N — середина ребра AC, точка O центр основания пирамиды, точка P делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.
а) Докажите, что прямая NP перпендикулярна прямой BS.
б) Найдите расстояние от точки B до прямой NP.
15.
i
Решите неравенство: 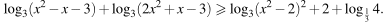
16.
i
В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у. е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
17.
i
Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC, перпендикулярна CM и пересекает катет AC в точке K. При этом AK : KC = 1 : 2.
а) Докажите, что 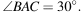
б) Пусть прямые MK и BC пресекаются в точке P, а прямые AP и BK — в точке Q. Найдите KQ, если BC = 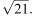
18.
i
При каких значениях параметра a уравнение
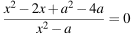
имеет ровно 2 различных решения.
19.
i
Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более 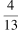 от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более
от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более 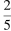 от общего числа учащихся группы, посетивших кино.
от общего числа учащихся группы, посетивших кино.
а) Могло ли быть в группе 10 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?
б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?
в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а) и б)?







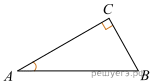 В треугольнике ABC угол C равен 90°,
В треугольнике ABC угол C равен 90°,  Найдите квадрат длины вектора
Найдите квадрат длины вектора  Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
 На рисунке изображён график функции
На рисунке изображён график функции 









