РЕШУ ЕГЭ — математика профильная
Вариант № 79337491
1.
i
 Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
2.
i
 Найдите сумму координат вектора
Найдите сумму координат вектора 
3.
i
В кубе  точка K — середина ребра
точка K — середина ребра  точка L — середина ребра
точка L — середина ребра  точка M — середина ребра
точка M — середина ребра  Найдите угол
Найдите угол  Ответ дайте в градусах.
Ответ дайте в градусах.
4.
i
В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по теме "Неравенства". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме "Неравенства".
5.
i
Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
6.
i
Найдите корень уравнения 
7.
i
Найдите значение выражения 
8.
i
 На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
9.
i
Перед отправкой тепловоз издал гудок с частотой  Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону
Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону  (Гц), где c − скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а
(Гц), где c − скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а  м/с. Ответ выразите в м/с.
м/с. Ответ выразите в м/с.
10.
i
Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
11.
i

На рисунке изображён график функции  Найдите
Найдите 
12.
i
Найдите наибольшее значение функции  на отрезке
на отрезке 
13.
i
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
14.
i
В правильной треугольной призме АВСА′B′C′ сторона основания АВ равна 6, а боковое ребро АА′ равно 3. На ребре АВ отмечена точка К так, что АК = 1. Точки М и L — середины рёбер А′С′ и В′С′ соответственно. Плоскость γ параллельна прямой АС и содержит точки К и L.
а) Докажите, что прямая ВМ перпендикулярна плоскости γ.
б) Найдите расстояние от точки С до плоскости γ.
15.
i
Решите неравенство: 
16.
i
Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние? Считайте, что перекресток не T-образный, обе дороги продолжаются за перекрестком.
17.
i
В остроугольном треугольнике ABC проведены высоты AP и CQ.
а) Докажите, что угол PAC равен углу PQC.
б) Найдите радиус окружности, описанной около треугольника ABC, если известно, что PQ = 8 и ∠ABC = 60°.
18.
i
Найдите все значения параметра а, при каждом из которых множество решений неравенства

содержит отрезок 
19.
i
Дима и Никита задумали по цифре и сообщили их Маше. Маша нашла сумму этих цифр, их разность, а затем перемножила все 4 числа. Мог ли полученный результат быть равен:
а) 1989?
б) 2012?
в) 2016?
Если нет — объясните, почему, если да — определите цифры, задуманные Димой и Никитой.
Просмотр содержимого документа
«ЕГЭ 2024 Декабрь Математика Вариант 7»
РЕШУ ЕГЭ — математика профильная
Вариант № 79337491
1.
i
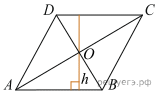 Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
2.
i
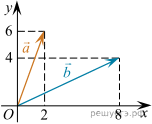 Найдите сумму координат вектора
Найдите сумму координат вектора 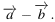
3.
i
В кубе 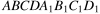 точка K — середина ребра
точка K — середина ребра 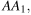 точка L — середина ребра
точка L — середина ребра 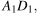 точка M — середина ребра
точка M — середина ребра 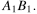 Найдите угол
Найдите угол 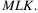 Ответ дайте в градусах.
Ответ дайте в градусах.
4.
i
В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по теме "Неравенства". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме "Неравенства".
5.
i
Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
6.
i
Найдите корень уравнения 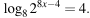
7.
i
Найдите значение выражения 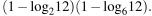
8.
i
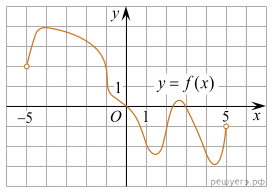 На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
9.
i
Перед отправкой тепловоз издал гудок с частотой 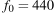 Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону
Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону 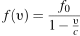 (Гц), где c − скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а
(Гц), где c − скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а 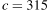 м/с. Ответ выразите в м/с.
м/с. Ответ выразите в м/с.
10.
i
Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
11.
i
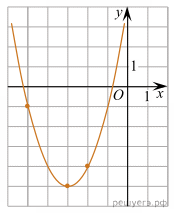 На рисунке изображён график функции
На рисунке изображён график функции 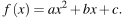 Найдите
Найдите 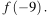
12.
i
Найдите наибольшее значение функции 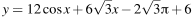 на отрезке
на отрезке 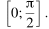
13.
i
а) Решите уравнение 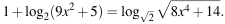
б) Найдите все корни этого уравнения, принадлежащие отрезку 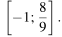
14.
i
В правильной треугольной призме АВСА′B′C′ сторона основания АВ равна 6, а боковое ребро АА′ равно 3. На ребре АВ отмечена точка К так, что АК = 1. Точки М и L — середины рёбер А′С′ и В′С′ соответственно. Плоскость γ параллельна прямой АС и содержит точки К и L.
а) Докажите, что прямая ВМ перпендикулярна плоскости γ.
б) Найдите расстояние от точки С до плоскости γ.
15.
i
Решите неравенство: 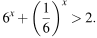
16.
i
Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние? Считайте, что перекресток не T-образный, обе дороги продолжаются за перекрестком.
17.
i
В остроугольном треугольнике ABC проведены высоты AP и CQ.
а) Докажите, что угол PAC равен углу PQC.
б) Найдите радиус окружности, описанной около треугольника ABC, если известно, что PQ = 8 и ∠ABC = 60°.
18.
i
Найдите все значения параметра а, при каждом из которых множество решений неравенства
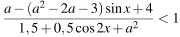
содержит отрезок 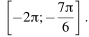
19.
i
Дима и Никита задумали по цифре и сообщили их Маше. Маша нашла сумму этих цифр, их разность, а затем перемножила все 4 числа. Мог ли полученный результат быть равен:
а) 1989?
б) 2012?
в) 2016?
Если нет — объясните, почему, если да — определите цифры, задуманные Димой и Никитой.







 Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба. Найдите сумму координат вектора
Найдите сумму координат вектора 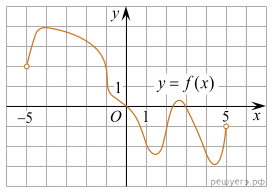 На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней. На рисунке изображён график функции
На рисунке изображён график функции 









