РЕШУ ЕГЭ — математика профильная
Вариант № 79337492
1.
i
 Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
2.
i
 На координатной плоскости изображены векторы
На координатной плоскости изображены векторы  и
и  Найдите длину вектора
Найдите длину вектора 
3.
i
От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
4.
i
В фирме такси в наличии 50 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на бортах, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
5.
i
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
6.
i
Решите уравнение  Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
7.
i
Найдите  если
если 
8.
i
 На рисунке изображён график некоторой функции
На рисунке изображён график некоторой функции  (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
(два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
9.
i
После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле  где h − расстояние в метрах, t − время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
где h − расстояние в метрах, t − время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
10.
i
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
11.
i
 На рисунке изображены графики функций
На рисунке изображены графики функций  и
и  которые пересекаются в точке A. Найдите ординату точки A.
которые пересекаются в точке A. Найдите ординату точки A.
12.
i
Найдите наименьшее значение функции  на отрезке
на отрезке 
13.
i
а) Решите уравнение 
б) Укажите все корни этого уравнения, принадлежащие промежутку 
14.
i
На рёбрах CD и BB1 куба ABCDA1B1C1D1 с ребром 12 отмечены точки Р и Q соответственно, причём DP = 4, а B1Q = 3. Плоскость APQ пересекает ребро CC1 в точке М.
а) Докажите, что точка М является серединой ребра CC1.
б) Найдите расстояние от точки С до плоскости APQ.
15.
i
Решите неравенство: 
16.
i
Пенсионный фонд владеет ценными бумагами, которые стоят 10t тыс. рублей в конце года t (t = 1, 2, ...). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 24%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце двадцатого года сумма на его счёте была наибольшей?
17.
i
Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K, так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.
а) Докажите, что CO = KO.
б) Найти отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет  площади трапеции ABCD.
площади трапеции ABCD.
18.
i
Найдите все значения параметра a, при каждом из которых система уравнений  имеет ровно два решения.
имеет ровно два решения.
19.
i
Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т. д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 2, 4, 6, 8, 10.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 5, 6, 8, 10, 11, 12, 13, 15, 17, 18, 19, 20, 22?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 8, 10, 15, 16, 17, 18, 23, 24, 25, 26, 31, 33, 34, 41.







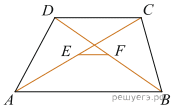 Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.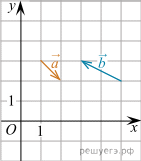 На координатной плоскости изображены векторы
На координатной плоскости изображены векторы 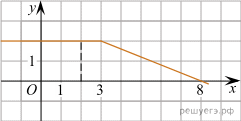 На рисунке изображён график некоторой функции
На рисунке изображён график некоторой функции 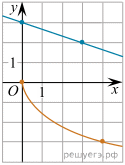 На рисунке изображены графики функций
На рисунке изображены графики функций 



















