Конспект урока по геометрии 9 класс на тему «Формулы дл вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности».
Цели урока:
Образовательная цель: вывести формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности, научить учащихся применять указанные формулы в процессе решения задач;
Развивающая цель: учиться анализировать – устанавливать причинно-следственные связи; сравнивать; обобщать; выдвигать гипотезы;
Воспитательная цель: воспитание эстетического отношения к окружающей действительности, явлениям, культуре;
Оборудование: интерактивная доска, презентация MS Power Point;
Тип урока: урок изучение нового материала с использованием технологии проблемного обучения; педагогики сотрудничества; информационно-коммуникационных технологий, здоровьесберегающих технологий, игровых технологий.
Ход урока:
I Актуализация:
Теоретический опрос.
Два ученика вызываются к доске для подготовки доказательства теорем о вписанной в правильный многоугольник и описанной около правильного многоугольника окружностях.
Фронтальный опрос (проводится в то время, пока у доски идет подготовка к доказательству теорем).
Какая формула используется для вычисления суммы углов выпуклого n-угольника?
Назовите формулу для вычисления угла правильного n-угольника?
Сформулируйте следствия из теорем о вписанной в правильный многоугольник и описанный около правильного многоугольника окружностях.
Что вы понимаете под словами центр правильного многоугольника?
Заслушать доказательства теорем, подготовленных у доски.
Индивидуальная работа по карточкам (данный этап работы происходит в то же время, что и фронтальный опрос).
I уровень (карточка № 1)
Найдите углы правильного восемнадцатиугольника.
Угол правильного n-угольника равен 108º. Вычислите количество его сторон.
Сколько сторон имеет правильный вписанный многоугольник, если дуга описанной окружности, которую стягивает его сторона, равна 45 º?
II уровень (карточка № 2)
Сумма углов правильного n-угольника равна 1440º. Чему равна сумма углов другого правильного многоугольника, если известно, что вершины первого многоугольника, взятые через одну, служат вершинами второго.
Докажите, что в правильном пятиугольнике ABCDE диагонали AC и AD делят угол BAE на три равные части.
III уровень (карточка № 3)
Вокруг правильного многоугольника описана окружность с радиусом 10 см, и в этот же многоугольник вписана окружность с радиусом, равным 5 см. Чему равно число сторон этого многоугольника?
В правильном многоугольнике диагонали MN и KE пересекаются в точке F так, что MF = 6 см, NF = 8 см, KE = 16 см. Найти KF и EF.
II Работа по теме урока (изучение новых понятий):
Вывод формул для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности можно организовать в два этапа.
Решение частной задачи (самостоятельно с последующим обсуждением решения).
Вывод формул в процессе решения задач на доказательство (один из учеников решает у доски, остальные в тетрадях).
Задача 1
В правильный шестиугольник вписана окружность радиуса 8 см.
Найдите:
Сторону шестиугольника;
Площадь шестиугольника;
Радиус описанной около него окружности.
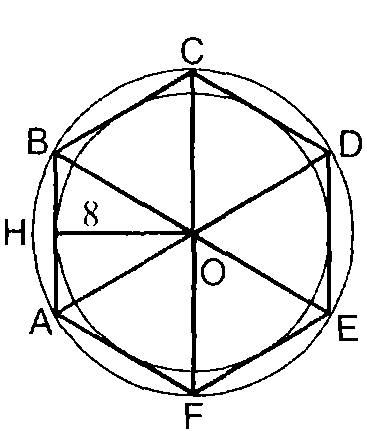
При необходимости можно использовать следующие подсказки и наводящие вопросы:
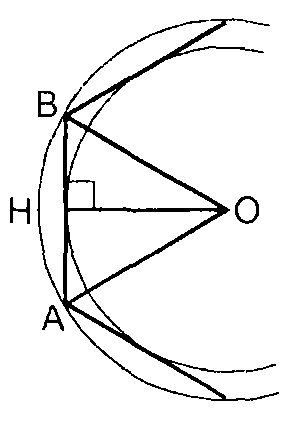
Разбейте ABCDEF на треугольники с общей вершиной O.
Чем является радиус OH вписанной в треугольник AOB окружности?
Чему равен угол AOB?
Вычислите градусную меру угла AOH.
Перечислите все известные элементы треугольника AOH. Как найти его неизвестные элементы?
Что можно сказать о площадях треугольников AOB, BOC, COD, DOE, EOF, FOA?
Задача 2
Докажите, что в правильном n-угольнике S=½Pr, 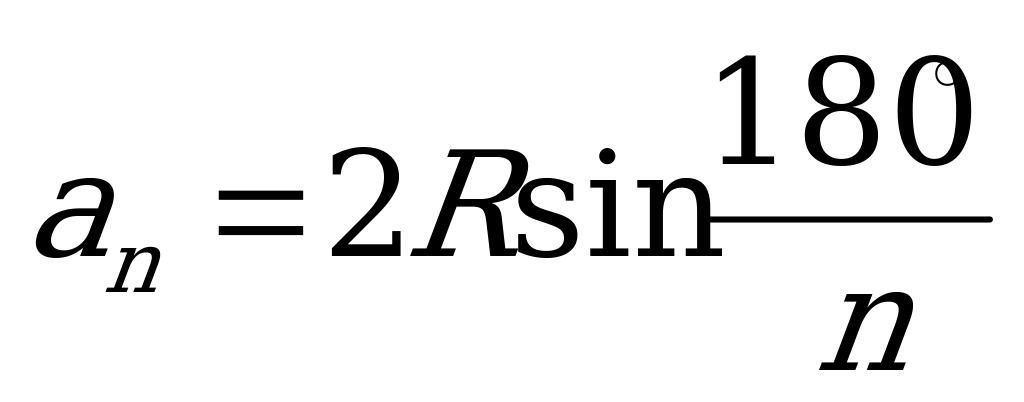 ,
,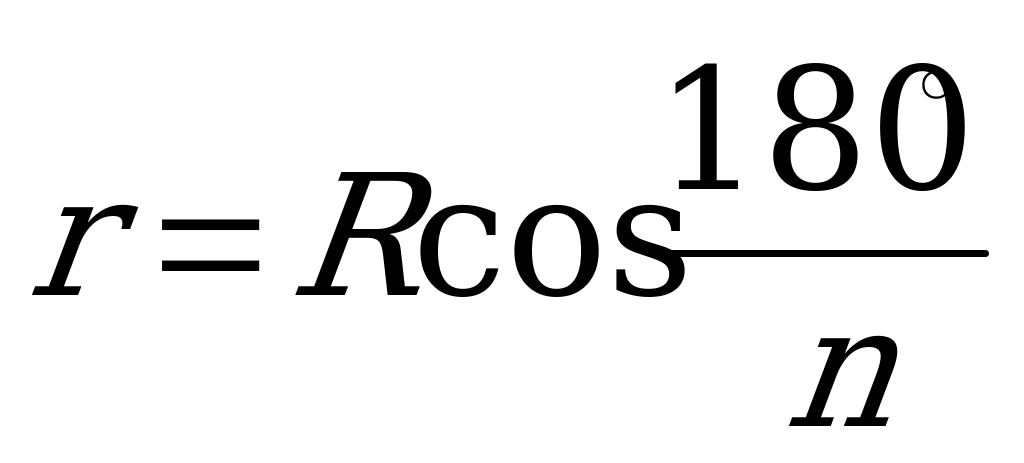 , где
, где 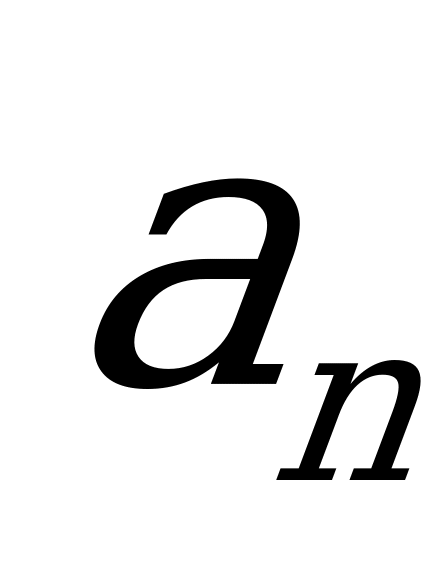 - сторона, r – радиус вписанной окружности, R – радиус описанной окружности, P – периметр, S – площадь многоугольника.
- сторона, r – радиус вписанной окружности, R – радиус описанной окружности, P – периметр, S – площадь многоугольника.
Чему равна площадь каждого треугольника, полученного при разбиении правильного n-угольника соединением центра данного n-угольника с его вершинами? (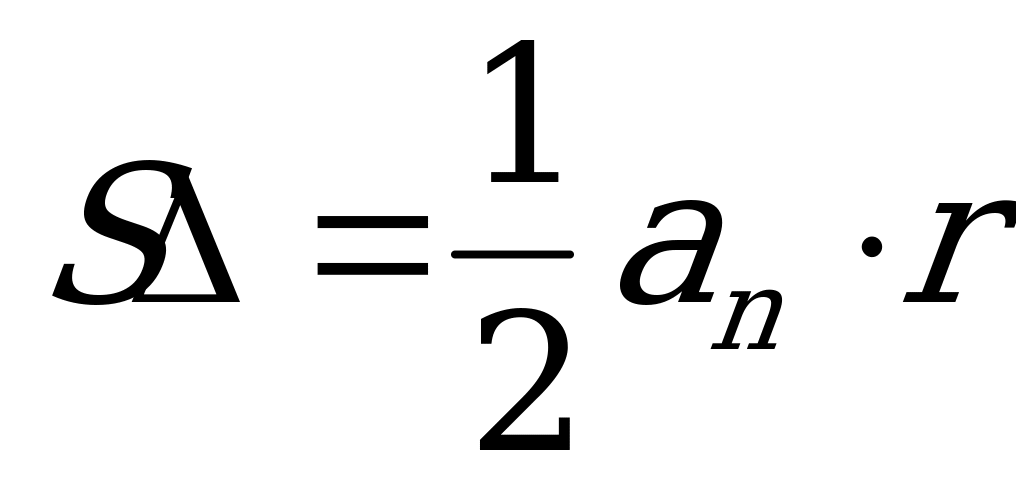 )
)
Найдите площадь всего n-угольника. (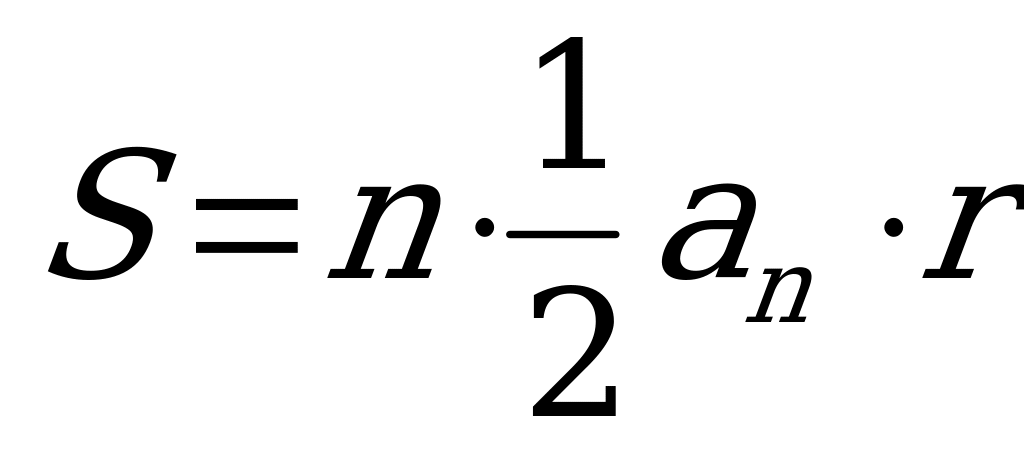 ) (1)
) (1)
Чему равно значение произведения 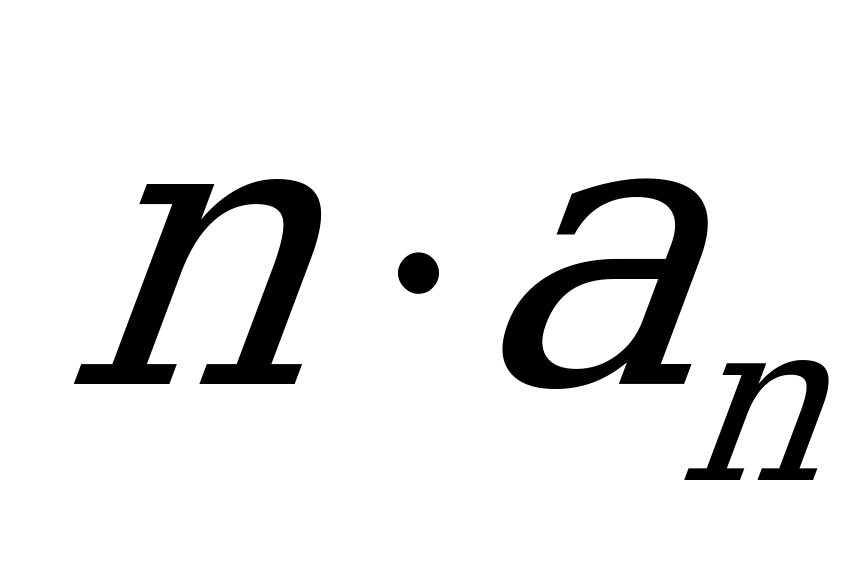 ? (
? (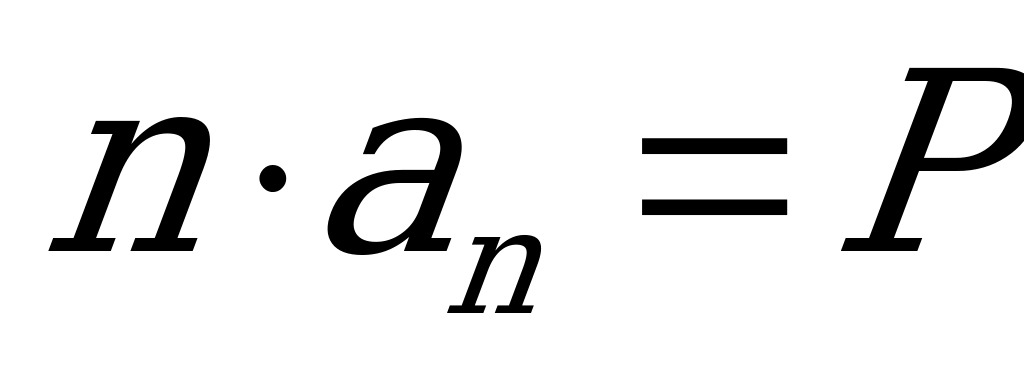 )
)
Как в этом случае можно записать формулу (1)? (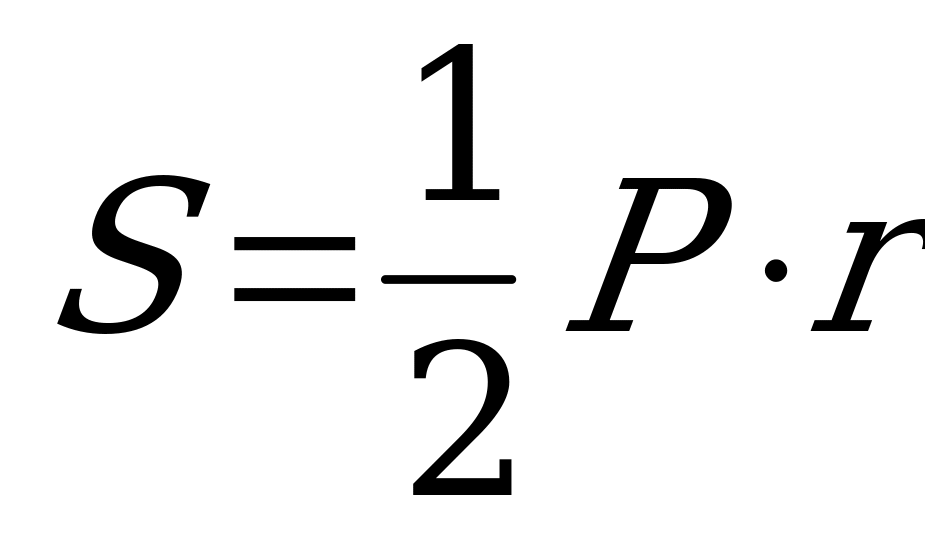 ).
).
Итак, формула для вычисления площади правильного многоугольника:
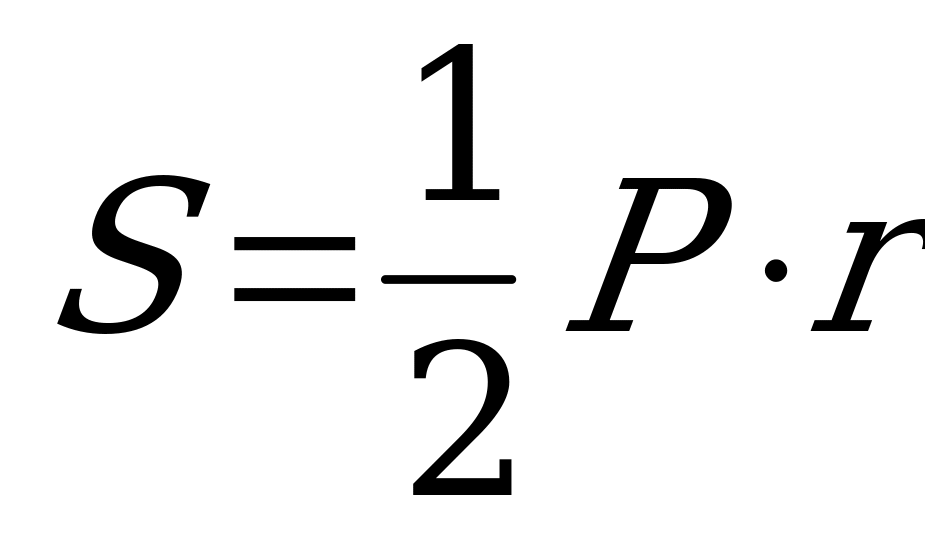 .
.
Итак, формулы для вычисления стороны правильного n-угольника и радиуса вписанной в него окружности:
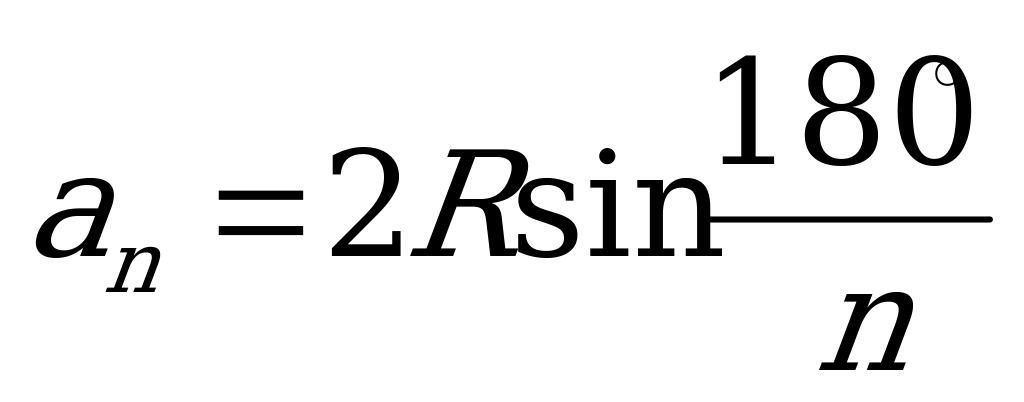
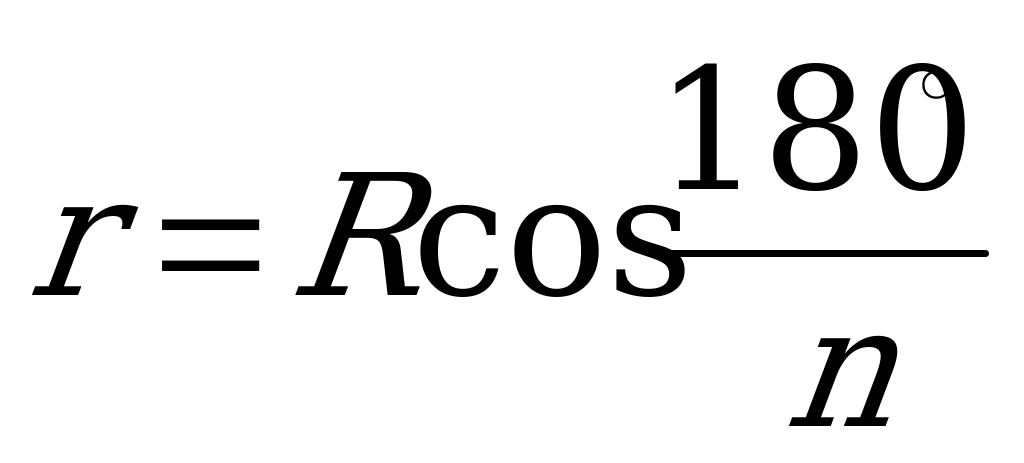
III Формирование умений и навыков:
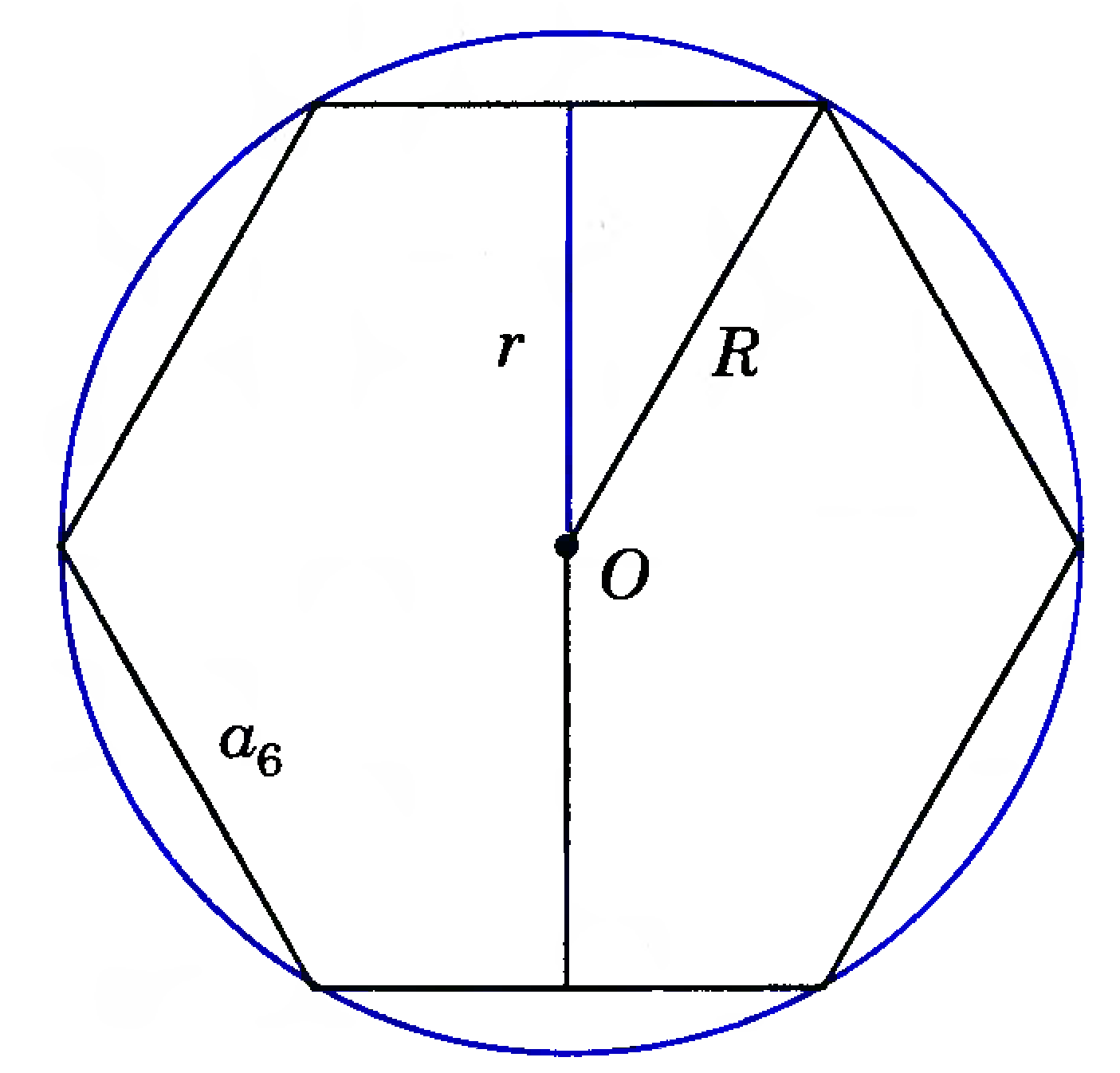
Задача №1:
На рисунке изображен правильный шестиугольник, вписанный в окружность радиуса R. Пусть  - сторона правильного шестиугольника, r – радиус вписанной окружности, P – периметр, S – площадь.
- сторона правильного шестиугольника, r – радиус вписанной окружности, P – периметр, S – площадь.
Найдите значение  , R,P и S, если
, R,P и S, если 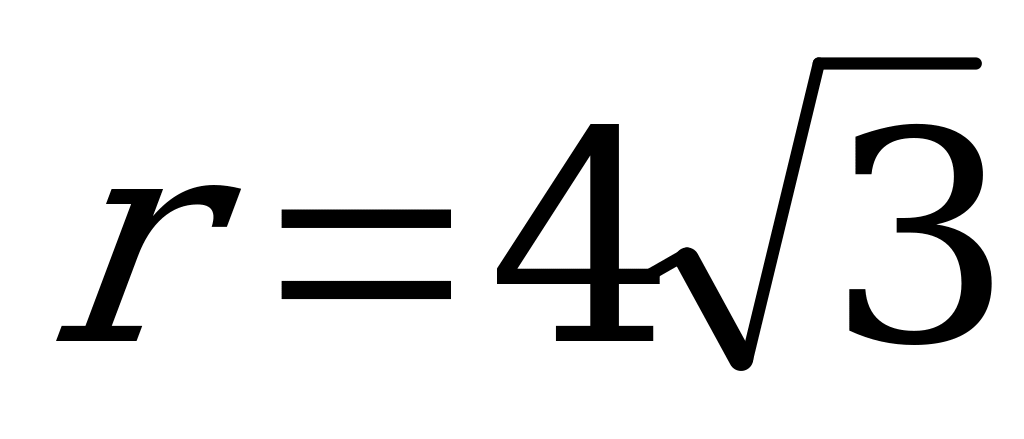 см.
см.
Решение. По условию 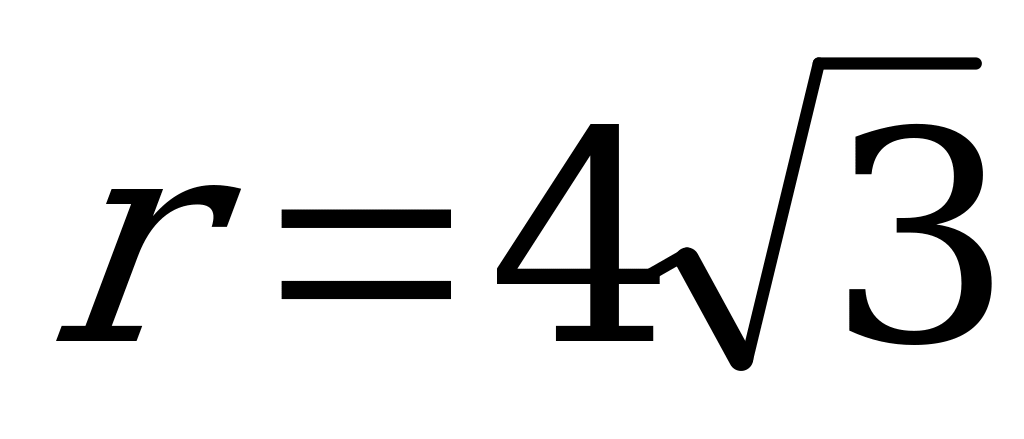 см, поэтому
см, поэтому
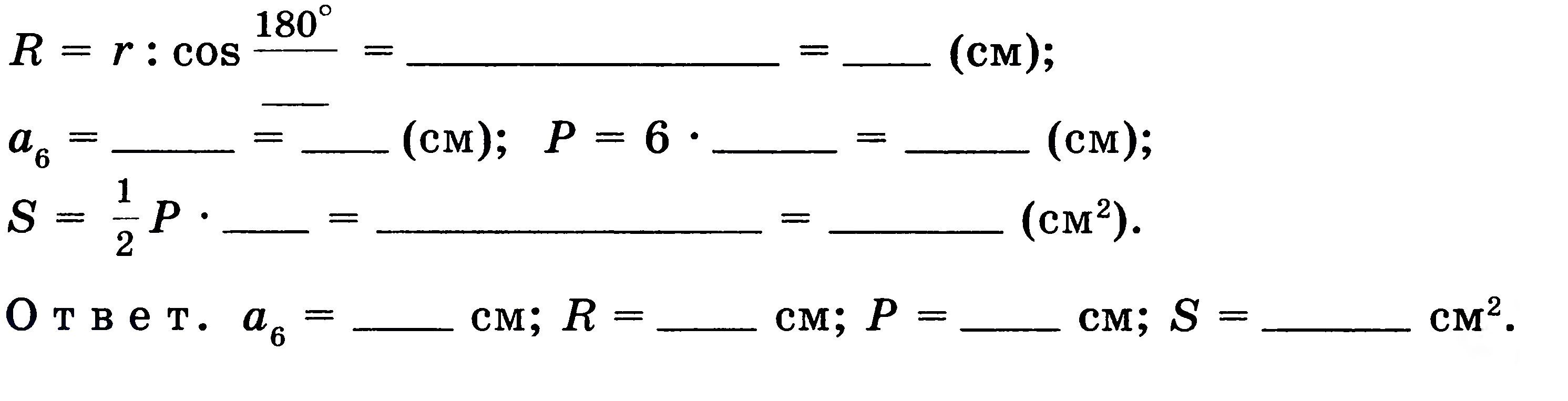
Задача №2(№1089 из учебника):
Квадрат вписан в окружность. Что нужно знать для определения стороны квадрата? (Для определения стороны квадрата нужно знать радиус описанной около него окружности).
Как по известному периметру треугольника можно вычислить радиус описанной около него окружности? (Найдем сторону треугольника, а затем используем формулу 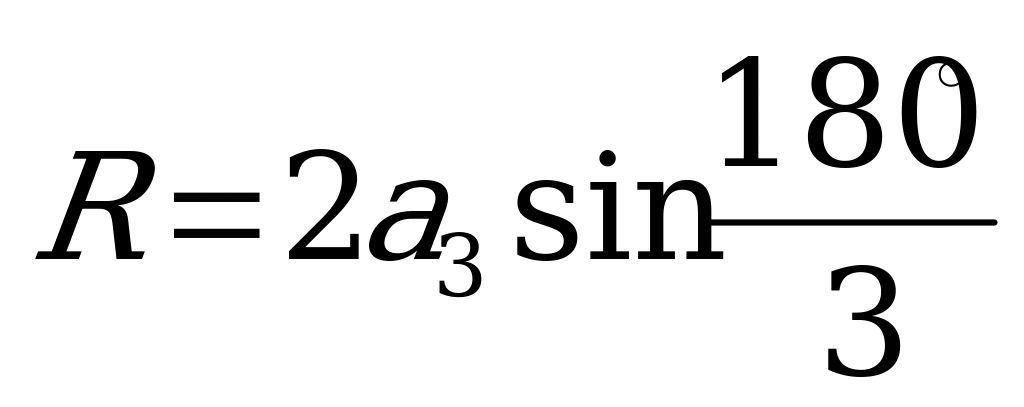 ).
).
Решение задачи:

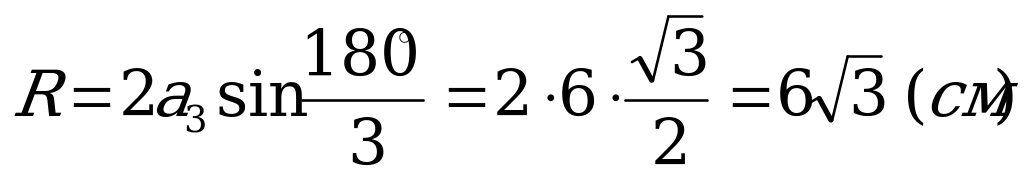
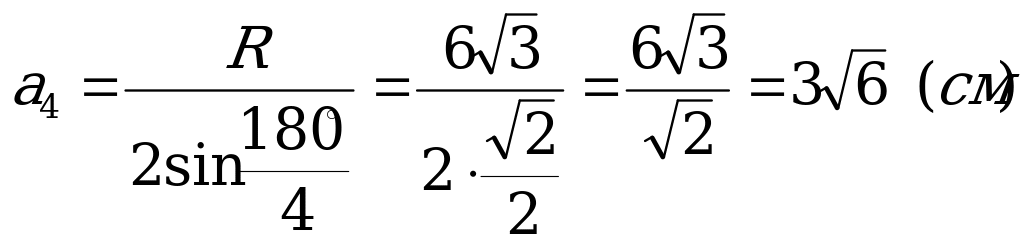
Дополнительная задача:
Центры двух окружностей расположены по разные стороны от их общей хорды, которая в одной из окружностей является стороной вписанного правильного четырехугольника, а другой – стороной вписанного правильного треугольника. Найдите расстояние между центрами этих окружностей, если длина указанной хорды равна 8 см.
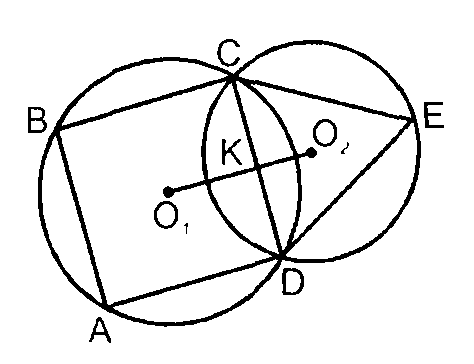
Решение: Хорда CD является одновременно стороной правильного четырехугольника и правильного треугольника, вписанных в окружности с центрами O1 и O2 соответственно. O1K и O2K – радиусы окружностей, вписанных в данные четырехугольник и треугольник.
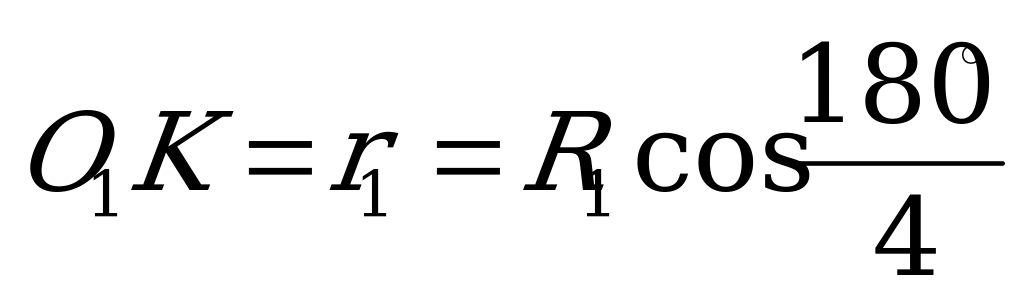 ,
,
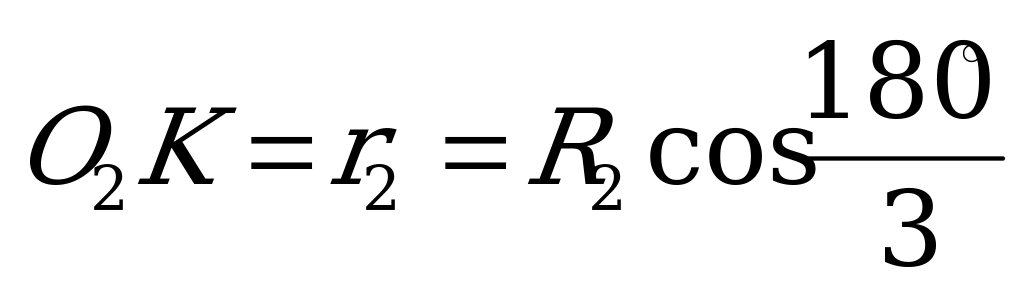 ,
,
где R1 и R2 – радиусы окружностей, описанных около данных четырехугольника и треугольника, то есть
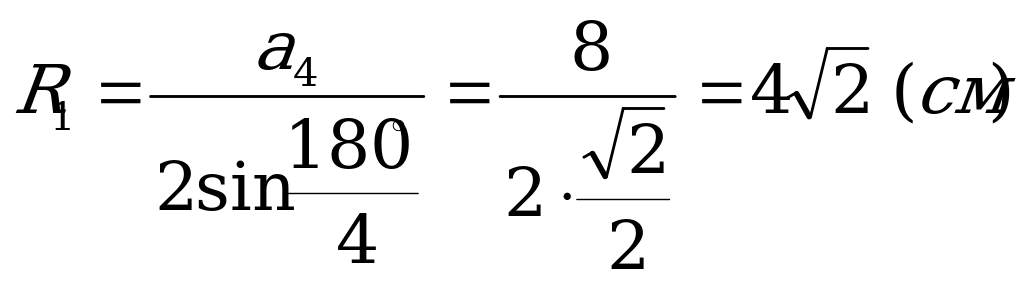
 ,
,
Тогда
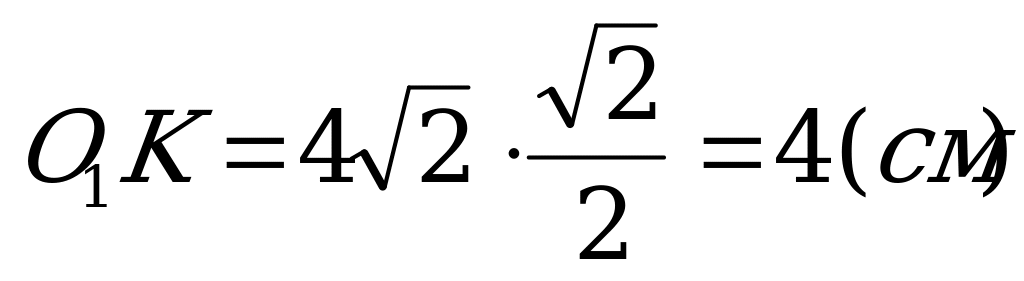
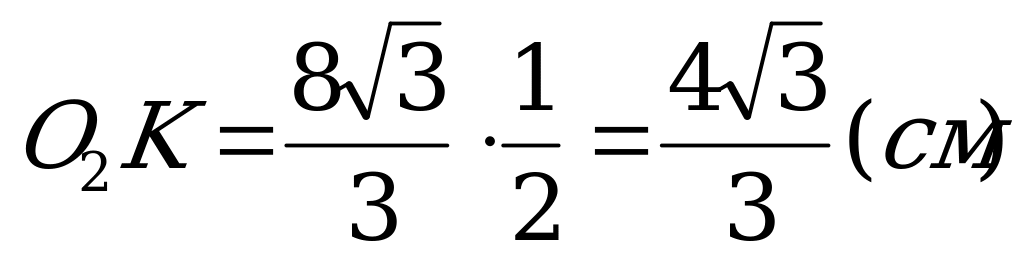
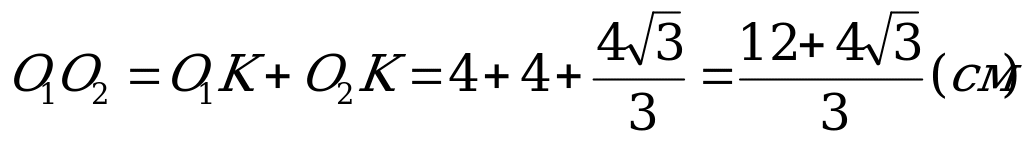
Ответ: 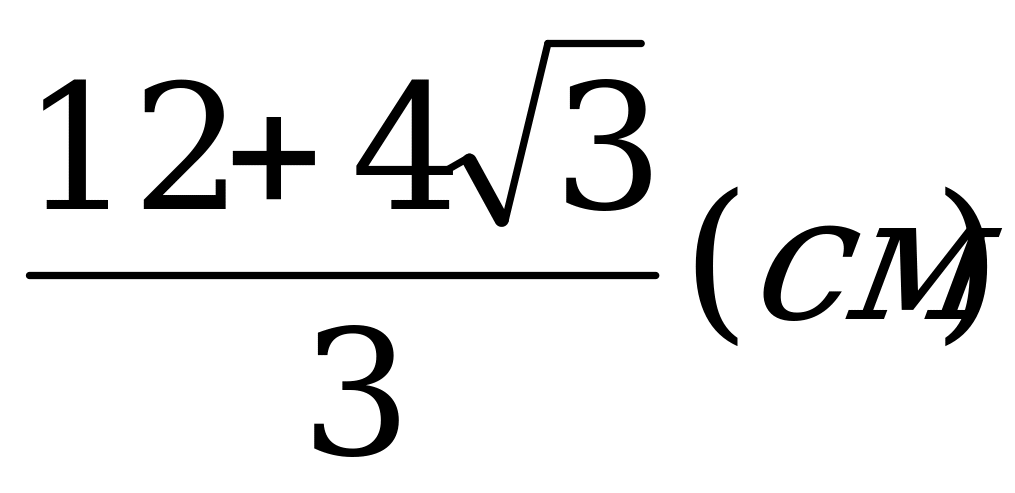
IV Подведение итогов урока.
V Домашнее задание. 1087 (3,5); 1088.
VI Оценка знаний (комментирование выставляемых оценок).










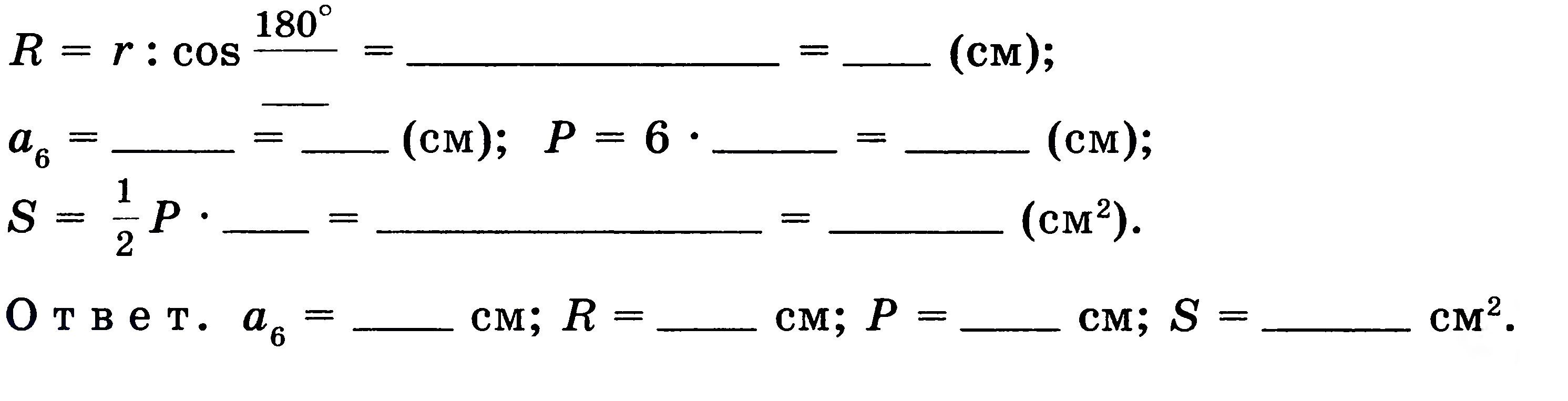
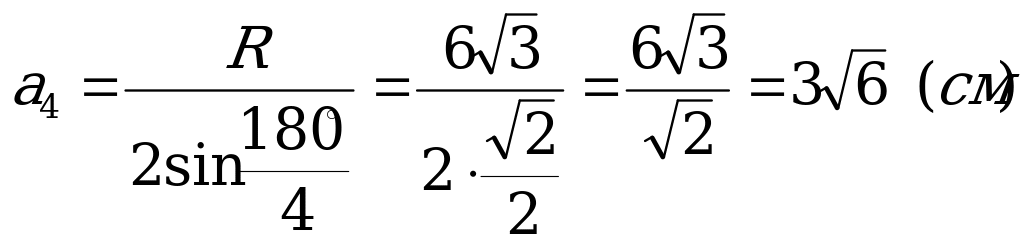
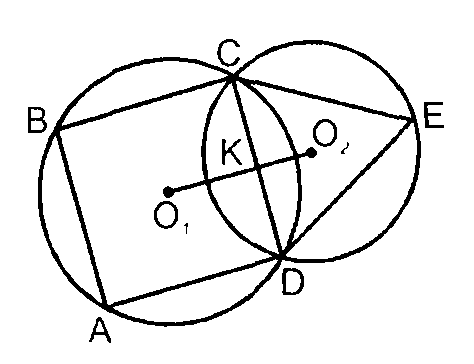
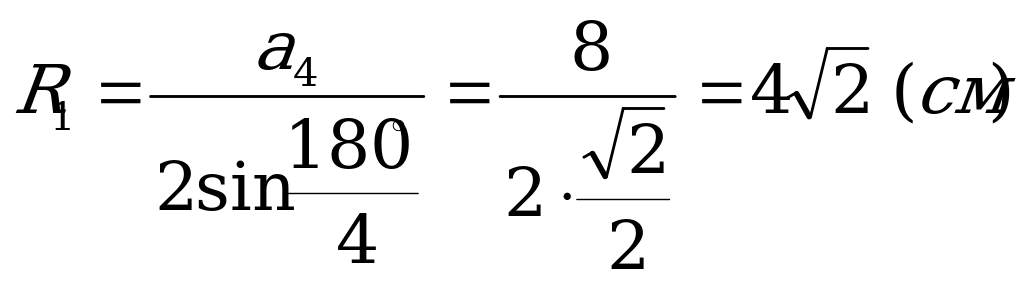
 ,
,









