"Геометрическая прогрессия" Алгебра 9 класс

ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ

Алгебра

9 класс

О ЗНАЧЕНИИ

• Геометрическая прогрессия играет большую и важную роль не только в школьном курсе алгебры, но и в дальнейшем обучении
• Важность этого небольшого раздела школьного курса заключается в его чрезвычайно широких областях применения

Известны телевизионные игры, в которых участник отвечает на предлагаемые ведущим вопросы, и за верные ответы ему по определенным правилам начисляется выигрыш.

Условия игры могут быть такими: за первый правильный ответ участнику начисляется 500р. , и с каждым следующим правильным ответом выигранная сумма увеличивается еще на 500р.

Таким образом, выигрыш растет в арифметической прогрессии:

500; 1000; 1500; 2000; 2500; 3000; …

Изменим условие игры: пусть за первый правильный ответ участник по-прежнему получает 500р., но с каждым следующим правильным ответом выигранная сумма удваивается

Теперь начисляемые игроку суммы образуют такую последовательность:

500; 1000; 2000; 4000; 8000; 16000; …

Это уже не арифметическая прогрессия: каждый следующий член последовательности получается из предыдущего умножением на одно и тоже число

ОПРЕДЕЛЕНИЕ

Геометрической прогрессией называют последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же не равное нулю число

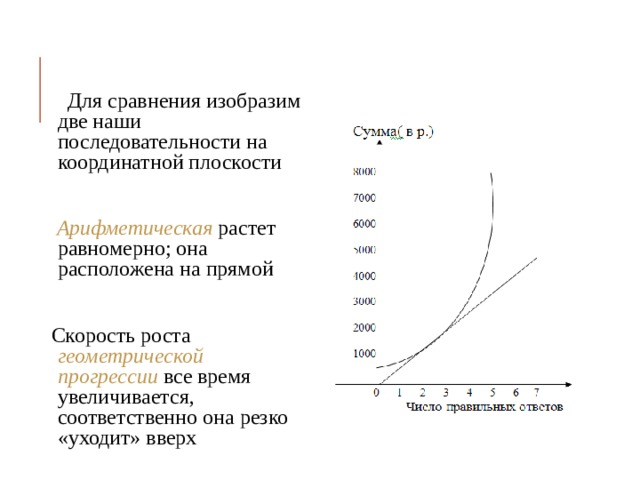
Для сравнения изобразим две наши последовательности на координатной плоскости

Арифметическая растет равномерно; она расположена на прямой

Скорость роста геометрической прогрессии все время увеличивается, соответственно она резко «уходит» вверх

ЗНАМЕНАТЕЛЬ

• Число на которое умножаются члены прогрессии, называют знаменателем геометрической прогрессии
• Его принято обозначать буквой q

РЕКУРРЕНТНЫЙ СПОСОБ

• Используя это обозначение, можно записать правило, по которому строится геометрическая прогрессия:

Формула n -го члена геометрической прогрессии

• Используя рекуррентную формулу, получим формулу n-го члена геометрической прогрессии

СВОЙСТВО ГП

• Квадрат любого члена геометрической прогрессии (кроме 1 и n ) равен произведению двух соседних с ним членов этой геометрической прогрессии (среднее геометрическое двух соседних членов)

ДОМАШНЕЕ ЗАДАНИЕ

• 1) § 24, ответить на вопросы 1–4
• 2) выполнить в тетради задания № 819, 821, 823
• 3) составить таблицу
• «Арифметическая и геометрическая прогрессии»

Определение

Арифметическая прогрессия

Геометрическая прогрессия

Переменные и обозначения

Способы задания прогрессии

Формула n -ого члена

Свойство прогрессии

Рекуррентный способ