Использование инновационных образовательных технологий в процессе обучения математике

Использование инновационных образовательных технологий

в процессе обучения математике

Вера Александровна Сороковикова,
учитель математики
УБ филиала РЭУ им. Г.В. Плеханова

Процесс развития школы, в отдельных направлениях ее работы, может осуществляться только как инновационный процесс: замена устаревших и неэффективных средств новыми для данных условий и более эффективными, использование новых идей, технологий.

Организация и управление этим процессом основывается на определенной базе, которая включает:

1. банк педагогических технологий, информационную базу из концепций, алгоритмов, учебно-методического обеспечения;

2. критерии выбора педагогической технологии, отправные позиции проектирования новой образовательной практики;

3. механизмы включения (использования, внедрения, освоения, выращивания) инновационной педагогической технологии в реальный учебно-воспитательный процесс.

В процессе обучения математике, я использую элементы современных образовательных технологий, в том числе информационно-коммуникационных, основываясь на теории оптимизации учебно-воспитательного процесса Ю.К.Бабанского, который предлагает следующие критерии оптимального выбора методов обучения:

1. соответствие методов основным целям обучения на данном этапе;

2. соответствие методов особенностям содержания обучения;

3. учет психологических возможностей детей;

4. учет уровня образовательной и воспитательной подготовленности детей;

5. учет особенностей групп и коллективов детей.

Для выбора инновационных технологий и направлений М.М.Поташника:

1. успехи и достижения современной науки о человеке;

2. государственные документы о развитии школы – государственный заказ;

3. передовой педагогический опыт;

4. собственный профессиональный опыт, интуицию.

При выборе элементов современных образовательных технологий анализирую:

1. совместимость технологии с моей технологией;

2. достаточная управляемость педагогической технологии;

3. оценка эффективности новой педагогической технологии в сравнении с имеющимися результатами.

Главное отличие технологии от методики в том, что методика – это совокупность рекомендаций учителю по проведению учебного процесса, любая технология же должна гарантировать конечный результат.

За годы работы мною разработана методическая система, позволяющая успешно решать одну из труднейших педагогических задач – приобщение каждого ученика к ежедневному напряженному умственному труду, воспитание познавательной самостоятельности как качества личности, укрепление в каждом ученике чувства собственного достоинства, уверенности в своих силах и способностях.

В своей педагогической технологии рассматриваю два основных этапа:

1. проектирование;

2. реализация проекта в учебном процессе.

Этап проектирования сосредоточен в «Рабочей программе» – паспорте проекта будущего учебного процесса в данном классе.

В поурочных планах представляю главные параметры учебного процесса:

- целеполагание;

- диагностика;

- дозирование домашнего задания;

- логическая структура урока;

- коррекция.

После составления «Рабочей программы» у меня появляются:

1. четкость;

2. структурность;

3. ясность методического языка;

4. обоснованная педагогическая технология в методике, которая помогает формированию методического ведения всего учебного процесса на весь учебный год.

Здесь формирую цели в форме: «знать», «уметь», «понимать», которые основываются на государственных документах, стандартах и программах.

В технологии «Диагностика» устанавливаю факт «достижения» (недостижения) цели. Учащиеся, не прошедшие диагностику, становятся участниками работы по коррекции. Диагностику провожу в письменном виде, дифференцируя по трем уровням. На уроке я спрашиваю только желающего отвечать или готового к ответу, чтобы ученик получил хорошую оценку, а я сэкономила время. Даю всем также возможность исправить оценку, так как оценка – стимул учения.

Особое внимание уделяю домашнему заданию, придерживаюсь принципов разумной дозировки, обеспечения индивидуального подхода, создания условий успешности.

Структуру представляю цепочкой уроков, которые разбиваю на группы по числу микроцелей. Каждая микроцель – это группа уроков, на которых, во-первых, должна быть достигнута микроцель, во-вторых, это программы развития мышления, памяти, речи, внимания, интереса и других качеств.

Из систем развивающего обучения Л.В. Занкова для проведения уроков применяю дидактические принципы:

1. ведущая роль теоретических занятий;

2. обучение на достаточно высоком уровне;

3. быстрый темп (укрупнение дидактических единиц) – разумное опережение;

4. хорошее осознание процесса обучения (ученик знает четко, что умеет и чему должен научиться);

5. дифференциация – обучать надо всех (комфортно каждому);

6. общее развитие.

Используя систему Л.В. Занкова, стараюсь с 5 по 11 класс учить детей без двоек и без принуждения, развивая у них устойчивый интерес к знаниям и делать учение радостным.

Для проведения уроков использую элементы педагогической технологии:

1. А.А. Окунева «Педагогическая технология на основе системы эффективных уроков»;

2. Р.Г. Хазанкина «Технология обучения математике на основе решения задач»;

3. В.Ф. Шаталова «Технология интенсификации обучения на основе схемных и

знаковых моделей учебного материала».

В центре педагогической концепции – личность ребенка, его творческое развитие в соответствии с индивидуальными природными способностями. Поэтому я свою технологию строю на основе личностной ориентации педагогического процесса, идеи авторских систем педагогов-новаторов.

Математика отличается от большинства других предметов тем, что на ее уроках очень много внимания уделяется решению задач. Задача становится одновременно и целью и средством обучения. Все проблемы я перевожу в плоскость задач: я разрабатываю методы оценки уровня сложности задач и методику, развивающие умение решать достаточно сложные задачи, считаю за аксиому то, что более активные виды учебной деятельности дают лучший результат. Отсюда следует принцип активизации учебной деятельности как один из ведущих принципов. Считаю, что работа над задачей является самым активным видом учебной математической деятельности, чем работа с учебником и слушание лекций. Задача – это не только умение, но также элемент знания. Работа в русле научного направления по «Формированию независимости мышления в ходе решения задач» всегда помогает мне в работе с учениками, я постоянно апробирую свои новые наработки и получаю положительный результат.

Начиная с 7 класса, каждый ученик ведет индивидуальные справочники по алгебре и геометрии. Так как есть целый ряд очень красивых и трудных задач, входящих в золотой фонд математики, ученики должны их знать и уметь решать. Поэтому ученики наравне с формулами, теоремами и методами решения задач вносят в справочник и их.

Для развития умственной деятельности использую приемы:

1. анализа;

2. классификации;

3. сравнения;

4. аналогии;

5. обобщений;

6. абстрагирований.

Учу, что для анализа необходимо:

1. применять дополнительные построения, нестандартные идеи для решения задач;

2. находить достаточные признаки, отбирать требуемый признак для решения задач;

3. применять нисходящий и восходящий анализ для решения задач.

Например: по геометрии с 7 класса начинаю учить анализу, который сразу дает решение:

1 . а) Доказать равенство треугольников б) Доказать равенство двух углов

… = … … = …

анализ решение анализ решение

= -равнобедренный

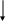СУС УСУ ССС

СУС ССС

УСУ

По условиям задачи учу делить их на типы: задачи на вычисление, на геометрические места точек, на максимум и минимум, на части, на уравнивание, на нахождение части от числа или числа по его части и т.д. Провести точную границу между задачами разных типов очень непросто, за счет простой переформулировки можно почти всегда перевести задачу с условием «доказать» в задачу с условием «найти». Обратное удается сделать гораздо реже. Наиболее привычны для учеников задачи на вычисление, так как они кажутся более простыми. Обучающую и развивающую роль этих задач трудно переоценить, через них в первую очередь происходит взаимодействие геометрии с математикой и алгеброй. Серьезным недостатком задач на вычисление является ответ, данный в учебнике или в «решебнике», так как, попадая в ситуацию ЕГЭ, некоторые ученики начинают страдать из-за невозможности сверить ответ. И тем не менее задачи на вычисление имеют достаточно высокий творческий потенциал. Как правило, перед учениками ставится задание «найти» и «Найти, что надо доказать». Важна еще одна особенность: для них можно предложить некую общую схему решения, схему поиска решения, методику обучения этому поиску и некоторые формальные признаки, по которым можно оценивать уровень сложности этих задач. Задача на вычисление лучше поддаются методической обработке, поэтому их я выбираю в качестве основного типа учебных задач. Это не означает, что задачи других типов менее важны.

Геометрическое развитие немыслимо без усвоения некоторого базового объема задач на построение, на геометрические места точек и других. Вначале задачи этих типов остаются на базовом уровне, и геометрическое развитие учеников идет за счет задач на вычисление, а задачи на доказательство провожу на достаточно высоком уровне геометрического развития.

Классификация задач по теме и по методу носит чисто учебный характер, ибо нельзя давать задачу с требованием решить ее именно таким методом, если возможен иной, более краткий, красивый и очень замаскированный метод ее решения. На уроках я знакомлю с общей классификацией методов решения задач: внутренние и внешние, общие и частные, алгебраические и геометрические.

Например:

Метод ключевого треугольника – общий и внутренний метод. Здесь я предлагаю несколько видов дополнительных построений:

1. соединить две точки отрезком;

2. продолжить отрезок прямой;

3. через данную точку провести прямую, параллельную данной или перпендикулярную данной

Так как большинство метрических теорем относится к геометрии треугольника, то при дополнительном построении увеличивается число треугольников. Считаю, что при решении задач ученики лучше видят и применяют метод ключевого треугольника, используя алгебраические методы.

Уровень математической подготовки ученика я свела к оценке уровня сложности задач, которые он умеет решать, при этом я рассматриваю не все множество задач, а мною отобранные его подмножества с указанием группы сложности. Я классифицирую задачи по трехуровневому принципу: А, В, С, тем самым стараюсь стимулировать учеников.

На уроках в качестве главного ведущего уровня выбираю – В, так как от него одна ступенька идет вверх, а другая – вниз.

Для уровня В составляю задачник – каталог соответствующий этому уровню. Если ученик решает 80% из заданных задач, даю сложную задачу, не входящую в каталог.

Работающая трехуровневая система задач является единой системой, так как они находятся во взаимодействии, при этом функцией нижних уровней является обслуживание верхних. На нижнем уровне подбираю задачи-детали, из которых на верхнем конструирую более трудные задачи. И наоборот, задачи верхнего уровня, за счет переформулировок, выделения отдельных частей адаптируются к нижнему уровню, растворяются в нем. Это взаимодействие происходит как по линии задач, так и по линии идей, то есть на нижнем уровне – одноидейные задачи, на верхнем – многоидейные. Думаю, что такая система задач выполняет не только оценочные, но и обучающие функции, то есть содержание определяет методику, но и методика влияет на содержание.

Способы мыслительной деятельности при изучении нового материала, при решении задач, при доказательстве теорем предусматривают действенное, образное, логическое мышление. Я предлагаю такие методы обучения, виды учебной деятельности, когда ученик сам формулирует определения того или иного понятия, формулирует теоремы, делает выводы, и обобщения в процессе и на этапе «открытия» новых знаний в ходе практической деятельности.

Должное внимание в своей работе уделяю выработке умений, навыков решать задачи. У меня выработана система работы над текстовыми задачами в младших классах, так как на этом этапе развиваются элементарные навыки абстрагирования, математического моделирования.

Арифметический метод решения задач является одним из лучших средств развития самостоятельного творческого мышления учащихся. Для этого специально подбираю задачи, чтобы показать красоту и простоту логического рассуждения, приводящего к решению. Таких задач очень много в учебниках под редакцией Г.В.Дорофеева и И.Ф. Шарыгина для учащихся 5-6 классов. Решая эти задачи, ученики накапливают определенный опыт работы с задачами: анализ условия, переформулировки условия, установление связей между величинами. Умение решать текстовые задачи практически совпадает с основами математической грамотности. Помимо простых есть много более сложных текстовых задач. Продвигаясь от элементарных к более сложным задачам, ученики подходят к профессиональной математике. Простые текстовые задачи полезны тем, кто не станет профессиональным математиком. М. Джонсон пишет: «В алгебре нет области, вызывающей у учащихся больше затруднений, чем решение текстовых задач».

Во время урока приглашаю к доске 4 учеников и диктую условия задачи сразу всем четверым. Задачи одинаковые, кроме одного параметра.

Задача: У Васи в копилке 100 монет, несколько монет по 3 копейки, а остальные у него по 5 копеек.

13 рублей / 16 рублей / 19 рублей / 22 рубля

Сколько у Васи монет по 3 коп., и сколько монет по 5 коп?

Требую четкости записи, если ввели переменную х, то ученик должен написать что это, так как хорошая запись заставляет их думать четче.

Если я запрещаю общаться во время контрольных работ, то во всех других случаях они могут и должны помогать друг другу. Если ученик у доски в растерянности, товарищ идет ему на помощь, и этот опыт полезен им обоим. Добиваюсь от учеников, что «Учеба – не соревнование», «Успех другого ученика – не твой провал» и «Провал твоего товарища – не твой успех».

После решения 4 вариантов анализирую их, разбирая разные методы.

Одна из трудностей которую я «подбрасываю» самым сильным ученикам – это «невозможные» задачи. Вызвав 4 человек, диктую условия.

Задача: В полдень Вася вышел пробежаться трусцой со скоростью 5 км/ч. Часом позже

Анна отправилась по тому же маршруту на велосипеде и догнала его в

4 км / 6 км / 8 км / 10 км

от дома. Какова была скорость Анны?

Все четверо берутся за решение, но у первого ответ отрицательный, а у троих положительный. Мы все проверяем вычисления и видим, что ошибки нет. Если один из учеников дает верное объяснение, то это прекрасно. Иногда приходится объяснять, что Анна только выехала, а Вася был уже в 5 км от дома. Так довожу до сознания учеников, что они должны уметь проверять вычисления, противоречащие здравому смыслу и при необходимости заявить, что ответа нет.

Важным является следующее:

1. научить учеников лучше понимать и использовать родной язык, чтобы точно передавать информацию;

2. развивать способность учеников представлять информацию с пользой для решения задач;

3. научить учеников разным способам представления: естественному языку, таблицам и графам;

4. улучшить их манеры (разборчивый почерк, результативное общение, включая умение объяснять и понять объяснение).

Для развития у учащихся навыков самостоятельности в поиске решения задач нужно четко соблюдать следующие этапы:

1. понимания постановки задачи;

2. план решения;

3. решение;

4. исследование полученного ответа.

При решении даже несложной задачи учащиеся часто много времени тратят на рассуждение о том, с чего начать? Учителю нужно уметь помочь им, найти путь к решению, поставив себя на место решающего, увидеть затруднения, направить его, при этом оставив посильную долю самостоятельной работы. Можно задать вопрос «Известна ли подобная, родственная задача?», «Найдите связь между данной задачей и задачей с известным решением или задачей, которая решается проще».

Рассматриваю вспомогательные задачи, которые могут помочь решить предложенную. Например. Вычислить сумму:

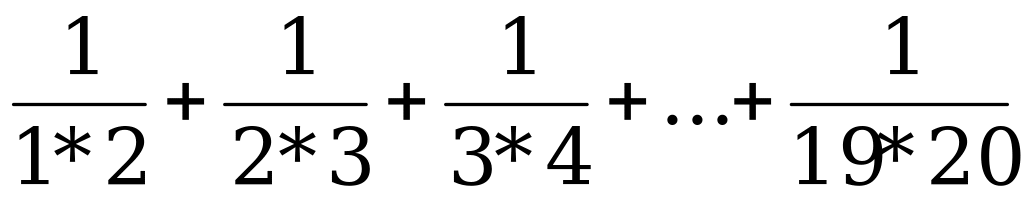
Вспомогательная задача. Придумайте несколько дробей, произведение которых равно их разности.

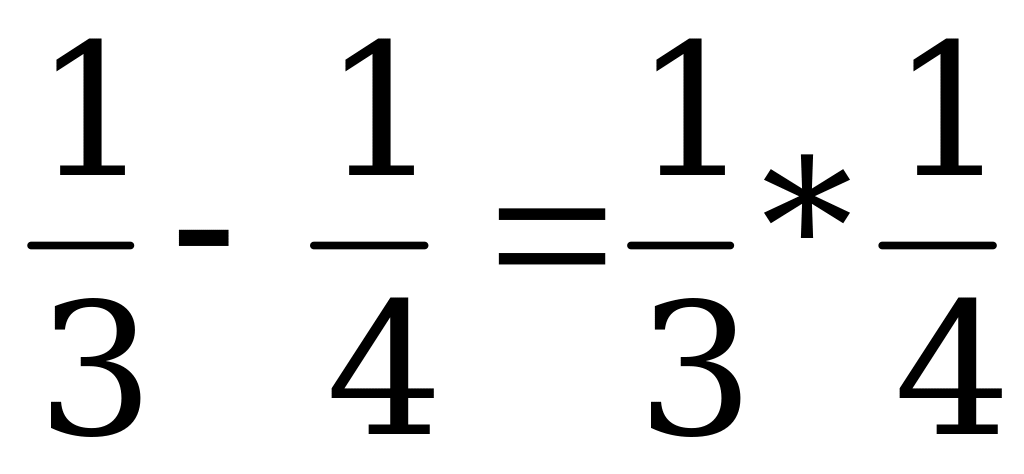
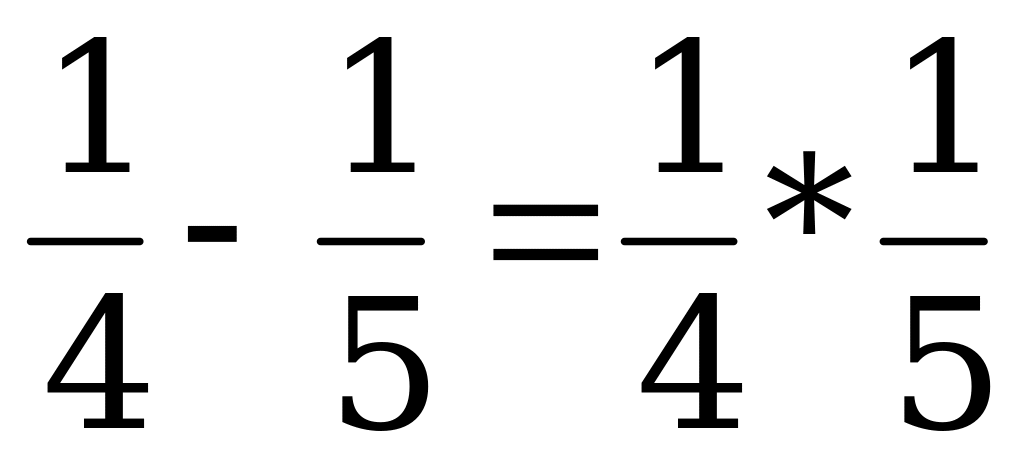
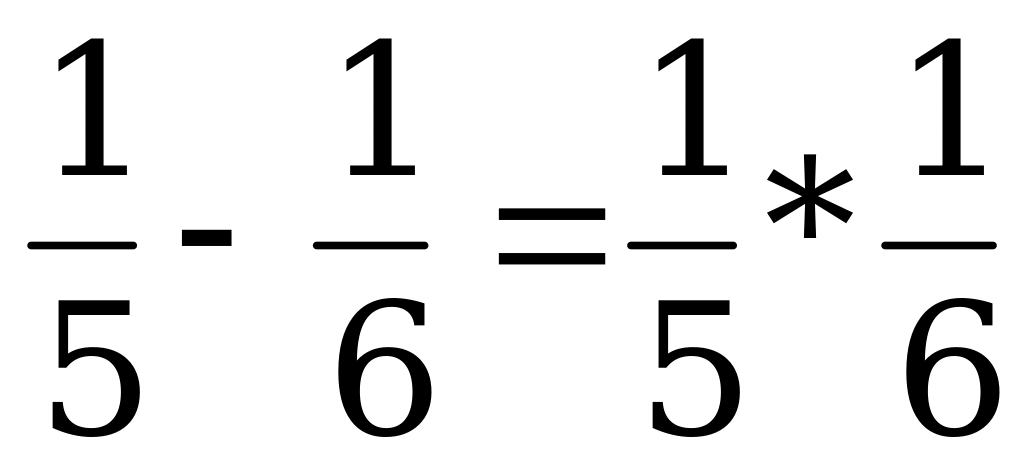
Используя вспомогательные задачи, ученики убеждаются в необходимости быть наблюдательными и учатся накапливать математические факты, установленные в результате решения задач.

При решении одних задач больше внимания уделяется обсуждению подходов к их решению, а при других – изучению полученных результатов.

Спрашиваю у ребят, чему полезному они научились в ходе решения задачи, какие новые знания приобрели, что полезно запомнить, как проверить результат, можно ли решить другим способом, при решении каких задач можно использовать данный метод.

Вывод: Любая задача должна быть заметным этапом в обучении школьников, ее решение должно формировать навыки самостоятельной работы, приемы умственной деятельности, учить методам поиска, открытия новых фактов и т.д. Моя педагогическая система позволяет успешно решать одну из труднейших педагогических задач – приобщение каждого ученика к ежедневному напряженному умственному труду, воспитание самостоятельности как качества личности, укрепление в каждом ученике чувства собственного достоинства, уверенности в своих силах и способностях.