| МБОУ «Средняя общеобразовательная школа № 48 им. Р.М. Каменева»
Исследовательский проект на тему:
«ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА»
Выполнил: Крутых Владислав, ученик 6 «а» класса. Проверил: Лопатина Ю.В., учитель математики.
КУРСК 2019 год
|
План
Введение………………………………………………………………………... 3
1. История возникновения положительных и отрицательных чисел………… 4
1.1. Положительные и отрицательные числа в древнем Китае, Индии, Греции, Египте и Европе……………………………………………………………………..…. 4
1.2. История возникновения знаков «плюс» и «минус»…....……………….... 7
1.3. Признание положительных и отрицательных чисел………………………. 8
2. Применение положительных и отрицательных чисел в различных сферах человеческой деятельности……………………………………………………………. 10
2.1. Положительные и отрицательные числа в медицине……………………. 10
2.2. Положительные и отрицательные числа в физике……………………….. 11
2.3. Положительные и отрицательные числа в истории………………….... 12
2.4. Положительные и отрицательные числа в географии…………………… 13
2.5. Положительные и отрицательные числа в повседневной жизни………... 14
Занимательные задачи…………………………………………………………….15
Заключение……………………………………………………………………….. 16
Список литературы………………………………………………………………. 17
Введение
Число является одним из главных понятий в математике. В современном мире человек постоянно пользуется числами, даже не задумываясь об их происхождении. Но без знания прошлого нельзя понять настоящее.
Понятие числа развивалось в тесной связи с изучением величин. Во всех разделах современной математики приходится рассматривать разные величины и пользоваться числами. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа изменялось, обогащалось и превратилось в важнейшее математическое понятие, с которым у людей возникало немало споров, особенно когда речь шла о нововведениях – появлении положительных и отрицательных величин.
Люди долго не могли привыкнуть к отрицательным числам, тем более признать их. Отрицательные числа казались им непонятными, ими не пользовались, просто не видели в них особого смысла. Рассмотрим историю их возникновения и развития, а также применение положительных и отрицательных чисел в разных сферах человеческой деятельности.
Цель: Изучить положительные и отрицательные числа: историю их возникновения и применение в разных сферах человеческой деятельности.
Задачи:
1. Изучить литературу по данной теме.
2. Понять суть положительных и отрицательных чисел.
3. Узнать о применении положительных и отрицательных чисел в разных сферах человеческой деятельности: медицине, физике, истории, географии и в повседневной жизни.
Объект исследования:
Области применения положительных и отрицательных чисел в жизни человека.
Предмет исследования: Положительные и отрицательные числа.
Метод исследования: чтение и анализ используемой литературы и наблюдения.
1. История возникновения положительных и отрицательных чисел
1.1. Положительные и отрицательные числа в древнем Китае, Индии, Греции, Египте и Европе
Первые сведения об отрицательных числах встречаются у китайских математиков во II в. до н. э. и то, были известны лишь правила сложения и вычитания положительных и отрицательных чисел; правила умножения и деления не применялись.
Положительные количества в китайской математике называли «чен», отрицательные – «фу»; их изображали разными цветами: «чен» - красным, «фу» - черным. Это можно заметить в книге «Арифметика в девяти главах» (Автор Чжан Цань). Такой способ изображения использовался в Китае до середины XII столетия, пока Ли Е не предложил более удобное обозначение отрицательных чисел – цифры, которые изображали отрицательные числа, перечеркивали черточкой наискось справа налево.
 Индийские математики в VII в. начали широко использовать отрицательные числа, но относились к ним с некоторым недоверием. Бхасхара прямо писал: "Люди не одобряют отвлеченных отрицательных чисел...". Вот как индийский математик Брахмагупта излагал правила сложения и вычитания: «имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество – долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму». «Сумма двух имуществ есть имущество».
Индийские математики в VII в. начали широко использовать отрицательные числа, но относились к ним с некоторым недоверием. Бхасхара прямо писал: "Люди не одобряют отвлеченных отрицательных чисел...". Вот как индийский математик Брахмагупта излагал правила сложения и вычитания: «имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество – долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму». «Сумма двух имуществ есть имущество».
(+х) + (+у) = +(х + у) (-х) + (-у) = - (х + у)
(-х) + (+у) = - (х - у) (-х) + (+у) = +(у - х)
0 – (-х) = +х 0 – (+х) = -х
Индийцы называли положительные числа «дхана» или «сва» (имущество), а отрицательные – «рина» или «кшайя» (долг). Индийские ученые, стараясь найти и в жизни образцы такого вычитания, пришли к толкованию его с точки зрения торговых расчетов. Если купец имеет 5000 р. и закупает товара на 3000 р., у него остается 5000 - 3000 = 2000, р. Если же он имеет 3000 р., а закупает на 5000 р., то он остается в долгу на 2000 р. В соответствии с этим считали, что здесь совершается вычитание 3000 - 5000, результатом же является число 2000 с точкой наверху, означающее «две тысячи долга». Толкование это носило искусственный характер, купец никогда не находил сумму долга вычитанием 3000 - 5000, а всегда выполнял вычитание 5000 - 3000.
Чуть позже в Древней Индии и Китае догадались вместо слов "долг в 10 юаней" писать просто "10 юаней", но рисовать эти иероглифы черной тушью. А знаков "+" и "–" в древности не было ни для чисел, ни для действий.
 Греки тоже поначалу знаков не использовали. Древнегреческий ученый Диофант вообще не признавал отрицательные числа, и если при решении уравнения получался отрицательные корень, то он отбрасывал его как "недоступный". И Диофант старался так сформулировать задачи и составлять уравнения, чтобы избежать отрицательных корней, но вскоре Диофант Александрийский стал обозначать вычитание знаком.
Греки тоже поначалу знаков не использовали. Древнегреческий ученый Диофант вообще не признавал отрицательные числа, и если при решении уравнения получался отрицательные корень, то он отбрасывал его как "недоступный". И Диофант старался так сформулировать задачи и составлять уравнения, чтобы избежать отрицательных корней, но вскоре Диофант Александрийский стал обозначать вычитание знаком.
Правила действий с положительными и отрицательными числами были предложены уже в III веке в Египте. Введение отрицательных величин впервые произошло у Диофанта. Он даже использовал специальный символ для них. В то же время Диофант употребляет такие обороты речи, как «Прибавим к обеим сторонам отрицательное», и даже формулирует правило знаков: «Отрицательное, умноженное на отрицательное, дает положительное, тогда как отрицательное, умноженное на положительное, дает отрицательное».
В Европе отрицательными числами начали пользоваться с XII–XIII вв., но до XVI в. большинство ученых считали их «ложными», «мнимыми» или «абсурдными», в отличие от положительных чисел – “истинных”. Положительные числа так же толковались как «имущество», а отрицательные – как «долг», «недостача». Даже знаменитый математик Блез Паскаль утверждал, что 0 − 4 = 0, так как ничто не может быть меньше, чем ничто.

 В Европе к идее отрицательного количества достаточно близко подошел в начале XIII столетия Леонардо Фибоначчи Пизанский. На состязании в решении задач с придворными математиками Фридриха II Леонардо Пизанскому было предложено решить задачу: требовалось найти капитал нескольких лиц. Фибоначчи получил отрицательное значение. "Этот случай, - сказал Фибоначчи, - невозможен, разве только принять, что один имел не капитал, а долг".
В Европе к идее отрицательного количества достаточно близко подошел в начале XIII столетия Леонардо Фибоначчи Пизанский. На состязании в решении задач с придворными математиками Фридриха II Леонардо Пизанскому было предложено решить задачу: требовалось найти капитал нескольких лиц. Фибоначчи получил отрицательное значение. "Этот случай, - сказал Фибоначчи, - невозможен, разве только принять, что один имел не капитал, а долг".
Однако в явном виде отрицательные числа применил впервые в конце XV столетия французский математик Шюке. Автор рукописного трактата по арифметике и алгебре «Наука о числах в трёх частях». Символика Шюке приближается к современной.
1.2. История возникновения знаков «плюс» и «минус»
Термины произошли от слов plus – «больше», minus – «меньше». Сначала действия обозначали первыми буквами p; m.
Возникновение современных знаков «+», «–» не совсем ясно. Знак «+», возможно, происходит от сокращенной записи et, т.е. «и». Впрочем, может быть он возник из торговой практики: проданные меры вина отмечались на бочке «–», а при восстановлении запаса их перечеркивали, получался знак «+».
В Италии ростовщики, давая деньги в долг, ставили перед именем должника сумму долга и черточку, вроде нашего минуса, а когда должник возвращал деньги, зачеркивали ее, получалось что-то вроде нашего плюса.
Современные знаки «+» и «–» появились в Германии в последнее десятилетие XVв. в книге Видмана, которая была руководством по счету для купцов (1489г.). Чех Ян Видман уже писал «+» и «–» для сложения и вычитания.
Чуть позднее немецкий ученый Михель Штифель написал «Полную Арифметику», которая была напечатана в 1544 году. В ней встречаются такие записи для чисел: 0-2; 0+2; 0-5; 0+7. Числа первого вида он назвал «меньше, чем ничего» или «ниже, чем ничего». Числа второго вида назвал «больше, чем ничего» или «выше, чем ничего». Вам, конечно, понятны эти названия, потому что «ничего» – это 0.
1.3. Признание положительных и отрицательных чисел
Признанию отрицательных чисел способствовали работы французского математика, физика и философа Рене Декарта. Он предложил геометрическое истолкование положительных и отрицательных чисел – ввел в 1637 году координатную прямую (рис. 1).
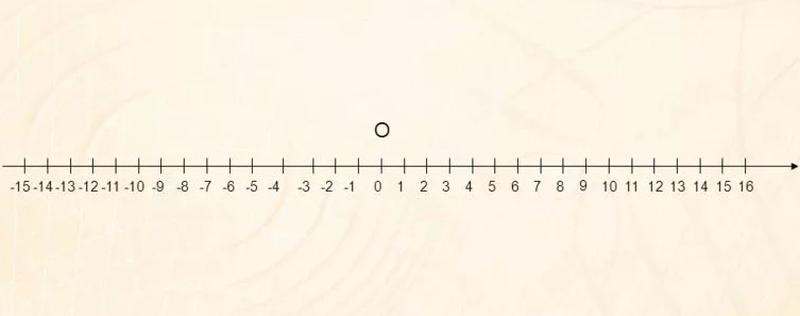
Рис. 1. Координатная прямая.
Положительные числа изображаются на числовой оси точками, лежащими вправо от начала 0, отрицательные – влево. Геометрическое истолкование положительных и отрицательных чисел способствовало их признанию.
 В 1544 году немецкий математик Михель Штифель впервые рассматривает отрицательные числа как числа, меньшие нуля (т. е. «меньшие, чем ничто»). С этого момента отрицательные числа рассматриваются уже не как долг, а совсем по-новому. Сам Штифель писал: «Нуль находится между истинными и абсурдными числами…»
В 1544 году немецкий математик Михель Штифель впервые рассматривает отрицательные числа как числа, меньшие нуля (т. е. «меньшие, чем ничто»). С этого момента отрицательные числа рассматриваются уже не как долг, а совсем по-новому. Сам Штифель писал: «Нуль находится между истинными и абсурдными числами…»
Почти одновременно со Штифелем защищал идею отрицательных чисел Бомбелли Раффаэле (около 1530—1572), итальянский математик и инженер, переоткрывший сочинение Диофанта.
Так же и Жирар считал отрицательные числа вполне допустимыми и полезными, в частности, для обозначения недостачи чего-либо.
Всякий физик постоянно имеет дело с числами: он всегда что-то измеряет, вычисляет, рассчитывает. Везде в его бумагах - числа, числа и числа. Если приглядеться к записям физика, то обнаружится, что при записи чисел он часто использует знаки "+" и "-". Например: термометр, шкала глубин и высот.
Только в начале XIX века теория отрицательных чисел закончила свое развитие, и отрицательные числа получили всеобщее признание.
2. Применение положительных и отрицательных чисел в различных сферах человеческой деятельности
2.1. Положительные и отрицательные числа в медицине
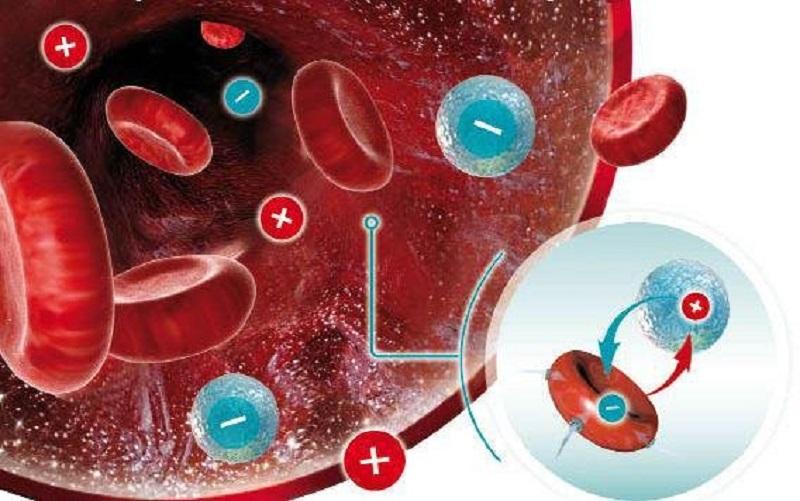 В трансфузиологии (науке о переливании крови) прежде чем перелить кровь человеку, для определения совместимости уточняется его резус-фактор Rh (врожденное групповое свойство эритроцитов, обусловленное наличием антигенов резус).
В трансфузиологии (науке о переливании крови) прежде чем перелить кровь человеку, для определения совместимости уточняется его резус-фактор Rh (врожденное групповое свойство эритроцитов, обусловленное наличием антигенов резус).
Почти 15% людей не обладают этим свойством, отчего их кровь именуется резус-отрицательной (Rh—).
 Офтальмологи тоже нашли применение отрицательным числам при лечении патологий глаза. Для получения отчетливого изображения на сетчатке глаза пациентам с нарушенным зрением приходят на помощь линзы, диоптрии которых могут быть не только положительными, но и отрицательными. Если линза собирает лучи в одну точку, она обозначается знаком «+», если она рассеивает их – со знаком «-». Симптомом миопии (близорукости) является снижение остроты зрения. Для того, чтобы пациент при близорукости мог четко видеть отдаленные предметы, окулист использует рассеивающие линзы с отрицательными диоптриями.
Офтальмологи тоже нашли применение отрицательным числам при лечении патологий глаза. Для получения отчетливого изображения на сетчатке глаза пациентам с нарушенным зрением приходят на помощь линзы, диоптрии которых могут быть не только положительными, но и отрицательными. Если линза собирает лучи в одну точку, она обозначается знаком «+», если она рассеивает их – со знаком «-». Симптомом миопии (близорукости) является снижение остроты зрения. Для того, чтобы пациент при близорукости мог четко видеть отдаленные предметы, окулист использует рассеивающие линзы с отрицательными диоптриями.
2.2. Положительные и отрицательные числа в физике
Физика - предмет, изучающий различные физические величины, описывающие разнообразные свойства окружающих нас предметов и явлений. Высота башни, расстояние от дома до школы, масса и температура человеческого тела, объем сосуда, скорость движущегося объекта, сила тока, мощность ядерного взрыва, электрический заряд металлического шарика, напряжение между двумя электродами – все это примеры физических величин. Физическую величину можно измерить. Например, с помощью рулетки (линейки), измеряют высоту зданий и расстояния от дома до учебного заведения. Термометры служат для измерения температуры, спидометры – для скорости автомобиля, рычажные весы - для массы тела.
 На шкале уличного термометра размечены только положительные числа, поэтому необходимо при указании численного значения температуры пояснение: «18 градусов тепла» (выше нуля). В физике для удобства применяется шкала с отрицательными числами: в случае, если на улице тепло, то температура воздуха выражается положительным числом, а если на улице холодно – отрицательным числом. Температура льда, снега также выражаются отрицательными значениями. Температура, при которой начинается таяние – 00С, при повышении температуры можно наблюдать нагревание и кипение.
На шкале уличного термометра размечены только положительные числа, поэтому необходимо при указании численного значения температуры пояснение: «18 градусов тепла» (выше нуля). В физике для удобства применяется шкала с отрицательными числами: в случае, если на улице тепло, то температура воздуха выражается положительным числом, а если на улице холодно – отрицательным числом. Температура льда, снега также выражаются отрицательными значениями. Температура, при которой начинается таяние – 00С, при повышении температуры можно наблюдать нагревание и кипение.
2.3. Положительные и отрицательные числа в истории
На сегодняшний день на уроках истории нам часто встречаются положительные и отрицательные числа, только их записывают не как «+» и «-», а в «нашей эре» и «до нашей эры».
Современный счет лет возник давно и связан с почитанием Иисуса Христа – основателя христианской религии. Счёт лет от рождения Иисуса Христа постепенно был принят в разных странах. В России этот счет принят царём Петром I триста лет назад. Время, исчисляемое от Рождества Христова, именуется «нашей эрой» (сокращённо н.э.). Продолжается наша эра две тысячи лет. Таким образом, «линию времени» можно представить в виде своеобразной координатной прямой (рис. 2).
До нашей эры Наша эра
753 74 1147 1799 2007
Основание Начало Первое упоминание о Москве Рождение А. С. Пушкина
Рима восстания
Спартака
Рис. 2. «Линия времени»
2.4. Положительные и отрицательные числа в географии
Физическая карта планеты является наиболее ярким примером использования отрицательных чисел в географии. 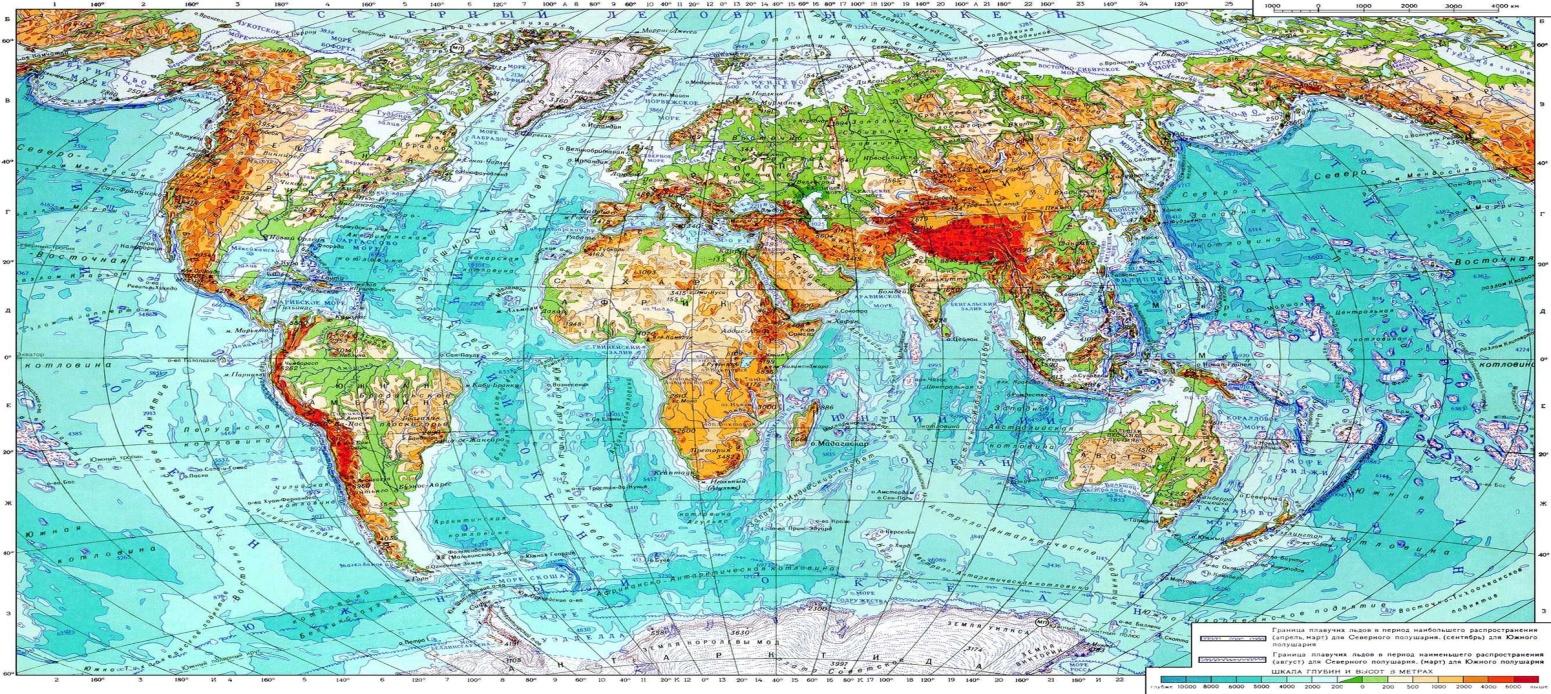
Участки суши на карте раскрашены различными оттенками зеленого и коричневого цветов, а моря и океаны изображены голубым и синим. Каждому цвету соответствует своя высота (для суши) или глубина (для морей и океанов). На картах приводится шкала глубин и высот, показывающая, какую высоту (глубину) означает тот или иной цвет. Положительные числа отвечают различным местам на суше, находящимся над поверхностью моря, отрицательные числа соответствуют точкам, находящимся ниже уровня моря.
В рассмотренной шкале высот за нулевую отметку принимается высота поверхности воды в Мировом океане. Эта шкала используется в геодезии и картографии. В отличие от этого, в быту обычно за нулевую высоту принимается высота поверхности земли.
Климат в той или иной точке Земли также характеризуется температурными значениями. Тепло ― градусы со знаком «плюс», холод ― градусы со знаком «минус».
2.5. Положительные и отрицательные числа в повседневной жизни
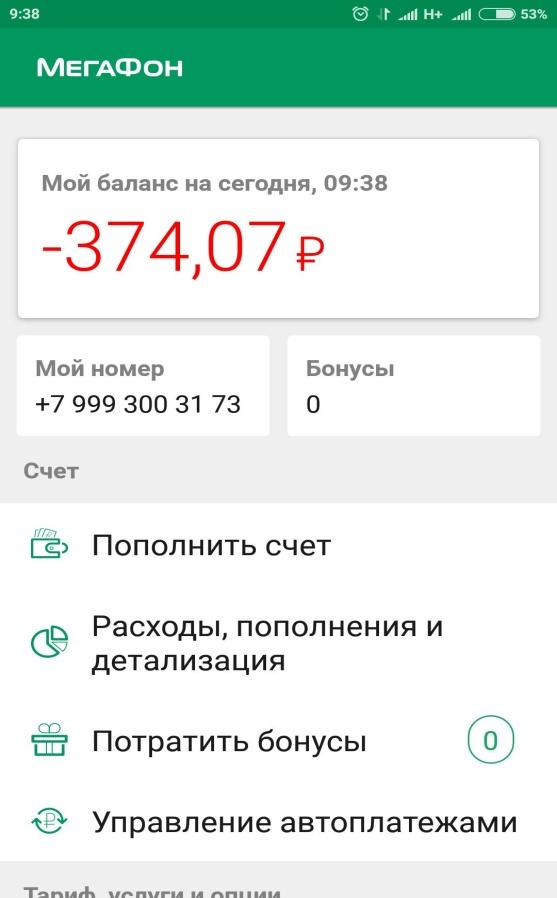
Проверяя баланс на своем телефоне, можно увидеть число со знаком «-». Это означает, что данный абонент имеет задолженность и не может осуществить звонок, пока не пополнит свой счет. Число же без знака «-» означает, что можно звонить или осуществлять какую-либо другую функцию.
Получая ежемесячно квитанции на оплату коммунальных услуг, можно увидеть суммы задолженности по оплате (со знаком «плюс») и суммы переплаты (со знаком «минус»). Это означает, что задолженность увеличивает сумму текущего платежа, а переплата – уменьшает.
Распродажа товаров в магазинах со скидками -50%, -70% всегда радует нас как покупателей.

Занимательные задачи
Задача 1

Задача 2
В морозилке была температура -10 градусов, ее повысили на 5 градусов, какая температура стала?
Решение: -10+5= -5
Ответ: Температура в морозилке стала -5 градусов.
Задача 3
 Птица клест-еловик несет яйца и высиживает птенцов зимой. Даже при температуре воздуха -35 градусов температура в гнезде не ниже 14 градусов. На сколько температура в гнезде выше температуры воздуха?
Птица клест-еловик несет яйца и высиживает птенцов зимой. Даже при температуре воздуха -35 градусов температура в гнезде не ниже 14 градусов. На сколько температура в гнезде выше температуры воздуха?
Решение: 14-(-35)=49
Ответ: Температура в гнезде на 49 градусов выше температуры воздуха.
Заключение
Работая над проектом, я осознал, что понять суть положительных и отрицательных чисел без истории их возникновения невозможно.
Изучив историю возникновения положительных и отрицательных чисел, можно сказать, что причиной их появления явились практические нужды людей. Отрицательные числа появились значительно позже положительных. Отрицательными числами обычно обозначали долг.
Работая с различными источниками, исследуя различные явления и процессы, я выяснил, что отрицательные и положительные числа широко используются в различных сферах деятельности человека. Данная тема является актуальной, находит широкое применение. Польза положительных и отрицательных чисел в науке и жизни человека разнообразна и велика.
Цель, поставленная мною в начале выполнения работы, достигнута, задачи выполнены.
Список литературы
1. Детская энциклопедия "Я познаю мир", Москва, "Просвещение", 1995 г.
2. «История древнего мира», 5 класс. Колпаков, Селунская.
3. Энциклопедия для детей. Т.11. Математика. Главный редактор М.Д. Аксенова, М., «Аванта +», 2002 г.
4. Зубарева И.И., Мордкович А.Г., Математика-6, М., «Мнемозина», 2005 г.
5. Депман И.Я. За страницами учебника математики, М., «Просвещение», 1989г.
6. Гнеденко Б.В. Энциклопедический словарь юного математика, М., «Педагогика –Пресс», 1999 г.
7. Интернет-ресурсы.







 Индийские математики в VII в. начали широко использовать отрицательные числа, но относились к ним с некоторым недоверием. Бхасхара прямо писал: "Люди не одобряют отвлеченных отрицательных чисел...". Вот как индийский математик Брахмагупта излагал правила сложения и вычитания: «имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество – долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму». «Сумма двух имуществ есть имущество».
Индийские математики в VII в. начали широко использовать отрицательные числа, но относились к ним с некоторым недоверием. Бхасхара прямо писал: "Люди не одобряют отвлеченных отрицательных чисел...". Вот как индийский математик Брахмагупта излагал правила сложения и вычитания: «имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество – долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму». «Сумма двух имуществ есть имущество». Греки тоже поначалу знаков не использовали. Древнегреческий ученый Диофант вообще не признавал отрицательные числа, и если при решении уравнения получался отрицательные корень, то он отбрасывал его как "недоступный". И Диофант старался так сформулировать задачи и составлять уравнения, чтобы избежать отрицательных корней, но вскоре Диофант Александрийский стал обозначать вычитание знаком.
Греки тоже поначалу знаков не использовали. Древнегреческий ученый Диофант вообще не признавал отрицательные числа, и если при решении уравнения получался отрицательные корень, то он отбрасывал его как "недоступный". И Диофант старался так сформулировать задачи и составлять уравнения, чтобы избежать отрицательных корней, но вскоре Диофант Александрийский стал обозначать вычитание знаком.
 В Европе к идее отрицательного количества достаточно близко подошел в начале XIII столетия Леонардо Фибоначчи Пизанский. На состязании в решении задач с придворными математиками Фридриха II Леонардо Пизанскому было предложено решить задачу: требовалось найти капитал нескольких лиц. Фибоначчи получил отрицательное значение. "Этот случай, - сказал Фибоначчи, - невозможен, разве только принять, что один имел не капитал, а долг".
В Европе к идее отрицательного количества достаточно близко подошел в начале XIII столетия Леонардо Фибоначчи Пизанский. На состязании в решении задач с придворными математиками Фридриха II Леонардо Пизанскому было предложено решить задачу: требовалось найти капитал нескольких лиц. Фибоначчи получил отрицательное значение. "Этот случай, - сказал Фибоначчи, - невозможен, разве только принять, что один имел не капитал, а долг". 
 В 1544 году немецкий математик Михель Штифель впервые рассматривает отрицательные числа как числа, меньшие нуля (т. е. «меньшие, чем ничто»). С этого момента отрицательные числа рассматриваются уже не как долг, а совсем по-новому. Сам Штифель писал: «Нуль находится между истинными и абсурдными числами…»
В 1544 году немецкий математик Михель Штифель впервые рассматривает отрицательные числа как числа, меньшие нуля (т. е. «меньшие, чем ничто»). С этого момента отрицательные числа рассматриваются уже не как долг, а совсем по-новому. Сам Штифель писал: «Нуль находится между истинными и абсурдными числами…» В трансфузиологии (науке о переливании крови) прежде чем перелить кровь человеку, для определения совместимости уточняется его резус-фактор Rh (врожденное групповое свойство эритроцитов, обусловленное наличием антигенов резус).
В трансфузиологии (науке о переливании крови) прежде чем перелить кровь человеку, для определения совместимости уточняется его резус-фактор Rh (врожденное групповое свойство эритроцитов, обусловленное наличием антигенов резус).  Офтальмологи тоже нашли применение отрицательным числам при лечении патологий глаза. Для получения отчетливого изображения на сетчатке глаза пациентам с нарушенным зрением приходят на помощь линзы, диоптрии которых могут быть не только положительными, но и отрицательными. Если линза собирает лучи в одну точку, она обозначается знаком «+», если она рассеивает их – со знаком «-». Симптомом миопии (близорукости) является снижение остроты зрения. Для того, чтобы пациент при близорукости мог четко видеть отдаленные предметы, окулист использует рассеивающие линзы с отрицательными диоптриями.
Офтальмологи тоже нашли применение отрицательным числам при лечении патологий глаза. Для получения отчетливого изображения на сетчатке глаза пациентам с нарушенным зрением приходят на помощь линзы, диоптрии которых могут быть не только положительными, но и отрицательными. Если линза собирает лучи в одну точку, она обозначается знаком «+», если она рассеивает их – со знаком «-». Симптомом миопии (близорукости) является снижение остроты зрения. Для того, чтобы пациент при близорукости мог четко видеть отдаленные предметы, окулист использует рассеивающие линзы с отрицательными диоптриями.  На шкале уличного термометра размечены только положительные числа, поэтому необходимо при указании численного значения температуры пояснение: «18 градусов тепла» (выше нуля). В физике для удобства применяется шкала с отрицательными числами: в случае, если на улице тепло, то температура воздуха выражается положительным числом, а если на улице холодно – отрицательным числом. Температура льда, снега также выражаются отрицательными значениями. Температура, при которой начинается таяние – 00С, при повышении температуры можно наблюдать нагревание и кипение.
На шкале уличного термометра размечены только положительные числа, поэтому необходимо при указании численного значения температуры пояснение: «18 градусов тепла» (выше нуля). В физике для удобства применяется шкала с отрицательными числами: в случае, если на улице тепло, то температура воздуха выражается положительным числом, а если на улице холодно – отрицательным числом. Температура льда, снега также выражаются отрицательными значениями. Температура, при которой начинается таяние – 00С, при повышении температуры можно наблюдать нагревание и кипение.



 Птица клест-еловик несет яйца и высиживает птенцов зимой. Даже при температуре воздуха -35 градусов температура в гнезде не ниже 14 градусов. На сколько температура в гнезде выше температуры воздуха?
Птица клест-еловик несет яйца и высиживает птенцов зимой. Даже при температуре воздуха -35 градусов температура в гнезде не ниже 14 градусов. На сколько температура в гнезде выше температуры воздуха?



















