Извлечение квадратных корней из чисел без калькулятора

«В математике следует помнить не формулы, а процесс мышления»

Е.И. Игнатьев

Извлечение квадратных корней из чисел без калькулятора.

Автор проекта:

ученик 8-а класса МОУ СОШ № 5

г. Миллерово Ростовской области

Андриенко Александр

Руководитель:

учитель математики

Хрущ Ольга Васильевна

Актуальность темы

• В школьном курсе математики часто встречаются задания с извлечением квадратного корня, в заданиях ОГЭ, в практических вычислениях и быту.

• Умения извлекать квадратные корни нужны при изучении некоторых тем химии и физики .

8/30/20

Извлечение квадратных корней из чисел без калькулятора

• Цель проекта :

Изучить способы извлечения квадратных корней из чисел без калькулятора.

• Задачи проекта :

1) изучить литературу по данному вопросу ;

2) исследовать способы извлечения квадратного корня;

3) показать практическое применение полученных знаний и оценить степень сложности в использовании различных способов и алгоритмов;

4) создать мини-книжечку по самым интересным способам извлечения квадратных корней из чисел.

• Объект исследования : математические символы – квадратные корни.
• Предмет исследования: способы извлечения корней из чисел без калькулятора.

8/30/20

Гипотеза

Способы извлечения квадратного корня из числа без калькулятора могут вызвать интерес у учащихся, найти практическое применение в учебной деятельности.

8/30/20

История квадратного корня

Знак корня происходит из строчной латинской буквы r ( начальной в лат. radix — корень ), сросшейся с надстрочной чертой: ранее, надчёркивание выражения использовалось вместо нынешнего заключения его в скобки.

видоизменённый способ записи выражения r

8/30/20

История квадратного корня

День квадратного корня отмечается 9 раз в столетие!

(в день, когда и число, и порядковый номер месяца являются

квадратными корнями из двух последних цифр года

(например, 5 мая 2025 года: 05-05-25)).

1 января хх01 года

2 февраля хх04 года

3 марта хх09 года

4 апреля хх16 года

5 мая хх25 года

6 июня хх36 года

7 июля хх49 года

8 августа хх64 года

9 сентября хх81 года

Рон Гордон

американский учитель,

Калифорния, США.

Промежуток (в годах) между праздниками составляет непрерывную последовательность нечётных чисел : 3, 5, 7 и т. д.

8/30/20

Приближенные методы извлечения квадратного корня

Способ использования таблицы квадратов двузначных чисел

Алгоритм:

1. цифра столбика десятков – это целая часть результата

2. цифра в сроке едини ц – это десятые

3. закрыть две последние цифры числа в таблице и найти число меньше подкоренного

Например: ≈ 8,6

Проверим на МК : ≈ 8,6023252

Плюсы: быстро, просто, доступно на экзамене.

Минусы:

• корни из чисел больше 100 этим способом извлечь невозможно;
• обязательно наличие таблицы квадратов.

Формула Древнего Вавилона

Алгоритм:

1. Представить число х в виде суммы: х = а 2 + b, где

а 2 ближайший к числу х точный квадрат натурального числа а.

2. Использовать формулу:

625

Проверим на МК : ≈ 8,6023252

Плюсы метода: даёт хорошее приближение

к точности вычисления корня.

Вавилонская табличка (около 1800—1600 г. до н. э.)

Минусы метода: нужно запомнить формулу.

Канадский метод

Например:

Х = 74, S = 81

Lakehead University -канадский государственный университет.

= 9 + (-= 8,612

Проверим на МК : ≈ 8,6023252

Плюсы метода: метод не сложный и удобный.

Минусы метода: - нужно знать формулу;

- его точность – не более двух – трёх знаков после запятой.

Метод Ньютона

метод итерации (с латинского iteratio - повторение)

Алгоритм:

1.   а 1   — первое приближение числа  (в качестве а 1  можно брать значения квадратного корня из натурального числа — точного квадрата, не превосходящего  х );

Исаак Ньютон

2. следующее, более точное приближение  а 2   числа 

найдется по формуле

3. третье, еще более точное приближение; …

4. (n+1)-е приближение  найдется по формуле

Герон

Александрийский

Например: а 1 = 8; а 2 = 8,625; а 3 = 8,602355 и т.д.

Проверим на МК : ≈ 8,6023252

Плюсы метода: позволяет извлекать квадратный корень из большого числа

с любой точностью.

Минусы метода: громоздкость вычислений.

Метод подбора угадыванием

(основан на подборе разных значений квадратов близких чисел

путём сужения области поиска)

Например:

1. Замечаем, что 8 2 = 64 и 9 2 = 81, значит, 8

2. Попробуем возвести 8,5 2 и вы получите 72,25.

3. Попробуйте 8,6 2 и вы получите 73,96

4. Попробуйте 8,7 2 и вы получите 75,69 74 .

Итак, 8,6

5. Попробуйте возвести 8,61 2 и вы получите 74,1321 74 .

6. Значит, 8,60

7. Продолжайте, пока не получите ответ достаточно точный для вас.

Университет Royal Holloway в Лондоне .

Минусы метода: требует многократного вычисления произведения столбиком не всегда правильно угаданных чисел; проигрывает в красоте решения и по времени.

8/30/20

Точные методы извлечения квадратного корня

Способ разложения на простые множители

Алгоритм: разложить число на простые множители и

извлечь квадратный корень из произведения.

Например:

291600│2

145 800│2

72 900│3

24 300│3

8 100│3

2 700│3

900│3

300│3

100│2

50│2

25│5

5│5

142129 = 13*13*29*29 ???

Минусы метода:

• нужно знать простые числа и признаки делимости;
• трудоёмкая задача;
• не всегда приводит к желаемому результату;

- занимает много времени.

Способ подбора

Суть метода —  чистый анализ.

Извлечём корень из 148996.

Такой дискриминант получается в задаче:

Теплоход проходит по течению реки до пункта назначения 336 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 48 часов после отплытия из него. Ответ дайте в км/ч.

Способ подбора

• Сначала определим — между какими числами (кратными ста) лежит наш результат: .

. Т.о., первая цифра - 3.

3. Далее смотрим, где «стоит» это число: ближе к или к ?

Число находится гораздо ближе к 360.

5. Проверяем число 380: х 380

380

3040

1140

144400

, так как  .

4. Проверим число 370: х 370

370

2590

1110

136900

, т.к. .

6. Проверяем число 390: х 390

390

3510

1170

152100  .

Способ подбора

7. Далее используются свойства произведений чисел. Известно, что:

• Произведение чисел, имеющих на конце 1 или 9, дают число с 1 в конце. 

Например, 21 * 21 =441.

• Произведение чисел, имеющих на конце 2 или 8, дают число с 4 в конце. 

Например, 18 * 18 = 324.

• Произведение чисел, имеющих на конце 5, дают число с 5 в конце. 

Например, 25 * 25 = 625.

• Произведение чисел, имеющих на конце 4 или 6, дают число с 6 в конце. 

Например, 26 * 26 = 676.

• Произведение чисел, имеющих на конце 3 или 7, дают число с 9 в конце. 

Например, 17 * 17 = 289.

Т. к. число заканчивается цифрой 6, то это либо , либо .

8. Проверяем: 384* 384 = 147456, 386*386 = 148996 . Значит, .

Минусы метода: требует многократного вычисления произведения столбиком

Извлечение квадратного корня уголком

Алгоритм:

1. Разбиваем число (5963364) на пары справа налево (5`96`33`64)

2. Извлекаем квадратный корень из первой слева группы (  - число 2). Так мы получаем первую цифру числа b.

3. Находим квадрат первой цифры (2 2 =4).

4. Находим разность первой группы и квадрата первой цифры (5-4=1).

5. Сносим следующие две цифры (получили число 196).

6. Удваиваем первую, найденную нами цифру, записываем слева за чертой (2*2=4).

7. Ищем вторую цифру числа b: удвоенная первая цифра, найденная нами, становится цифрой десятков числа, при умножении которого на число единиц, необходимо получить число меньшее 196 (это цифра 4, 44*4=176). 4 - вторая цифра числа b.

8. Находим разность (196-176=20).

9. Сносим следующую группу (получаем число 2033).

10. Удваиваем число 24, получаем 48.

11. 48 десятков в числе, при умножении которого на число единиц, мы должны получить число меньшее 2033 (484*4=1936). Найденная нами цифра единиц (4) и есть третья цифра числа b.

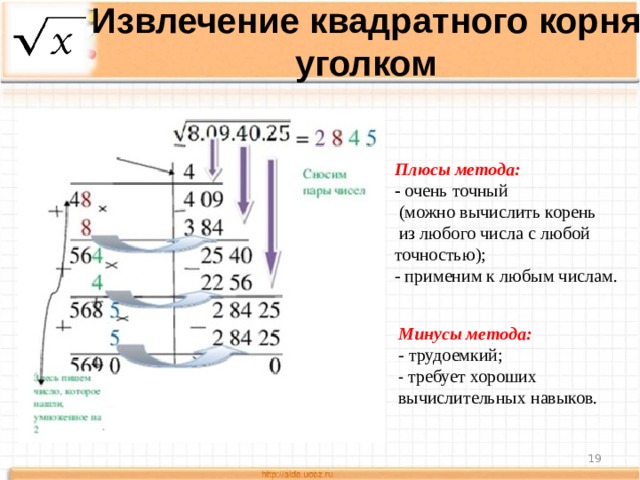
Извлечение квадратного корня уголком

Плюсы метода:

- очень точный

(можно вычислить корень

из любого числа с любой точностью);

- применим к любым числам.

Минусы метода:

- трудоемкий;

- требует хороших

вычислительных навыков.

Выводы

8/30/20

«Умственную самодеятельность, сообразительность и «смекалку» нельзя ни «вдолбить», ни «вложить» ни в чью голову. Результаты надёжны лишь тогда, когда введение в область математических знаний совершается в лёгкой и приятной форме, на предметах и примерах обыденной и повседневной обстановки, подобранных с надлежащим остроумием и занимательностью».

Е. И. Игнатьев

(1908 год)

8/30/20

Спасибо за внимание

8/30/20