"Комбинаторика: перестановки, размещения, сочетания"

Комбинаторика.

Перестановки.

Размещения.

Сочетания.

Подготовила преподаватель математики Абибуллаева А.С.

05/22/2023

План:

• Что такое комбинаторика? Правило суммы. Правило произведения. Перестановки
• Что такое комбинаторика? Правило суммы. Правило произведения. Перестановки
• Что такое комбинаторика?
• Правило суммы.
• Правило произведения.
• Перестановки

• Размещения Сочетания
• Размещения Сочетания
• Размещения
• Сочетания

1. Комбинаторика.

• Комбинаторика – радел математики, в котором рассматриваются задачи о подсчёте числа комбинаций составленных по определённым правилам.

Обычный вопрос в комбинаторных задачах: сколькими способами...

К комбинаторным задачам также относятся задачи построения математических квадратов, задач расшифровки и кодирования.

Основные правила комбинаторики – это правила суммы и произведения.

Рождение комбинаторики как раздела математики связано с трудами великих французских математиков 17 века

Пьера Ферма

(1601-1665)

Блеза Паскаля

(1623-1662)

по теории азартных игр

2. Правило суммы

Если некоторый элемент А можно выбрать m способами, а элемент В - n способами, то выбор «либо А, либо В» можно сделать m+n способами.

Запись в тетради:

А - m способов;

В - n способов;

А или В - (m+n) способов.

Пример: если на тарелке лежат 5 яблок и 6 груш, то один плод можно выбрать 5+6=11 способами.

Обратите внимание на то, что выбирается не просто яблоко или груша, а один конкретный плод это яблоко или эта груша.

3. Правило произведения.

Если элемент А можно выбрать m способами, элемент В можно выбрать n способами, то пару А и В можно выбрать m·n способами.

Запись в тетради .

А — m способов;

В - n способов;

(А и В) - (m·n) способов.

Пример: если есть 2 разных конверта, 3 разные марки, то выбрать то выбрать конверт и марку можно 2*3=6 способами. Обратите внимание - выбирается пара конверт и марка. Правило произведения верно и в том случае, когда рассматриваются элементы нескольких множеств.

Задача усно.

На блюде лежат 7 яблок 3 груши и 4 апельсина

• а) сколькими способами можно взять с блюда 1 плод;
• б) сколькими способами можно взять: (яблоко с грушей); (яблоко с апельсином); (грушу с апельсином);
• в) сколькими способами можно взять 2 фрукта с разными названиями.

Решение:

• а) выбирается 1 плод. Правило суммы 7+3+4=14;
• б) выбирается 2 плода. Правило произведения: (7 . 3=21 способ ),

(7 . 4=28 способов ),

(3 . 4=12 способов );

• в) применяются оба правила. Сначала - правило произведения (выбирается пара) и затем – правило суммы (эта пара рассматривается как единое целое) 7 . 3+7 . 4+3 . 4=21+28+12=61 (способ ).

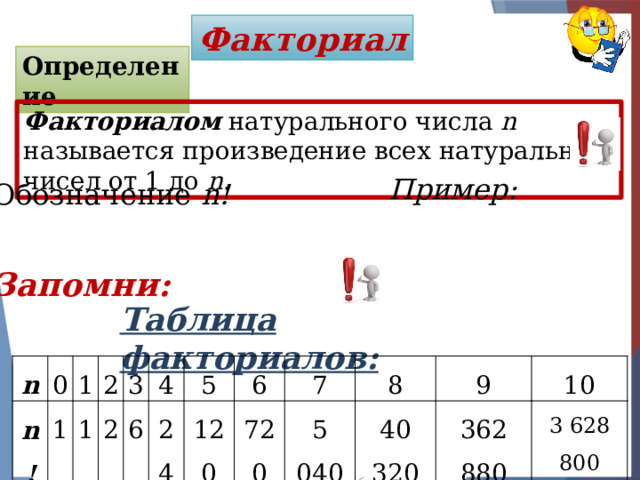
Факториал

Определение

Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n .

Пример:

Обозначение n!

Запомни:

Таблица факториалов:

n

0

n!

1

1

2

1

3

2

6

4

5

24

6

120

7

720

5 040

8

9

40 320

10

362 880

3 628 800

На примерах учимся

Найдите значение выражения

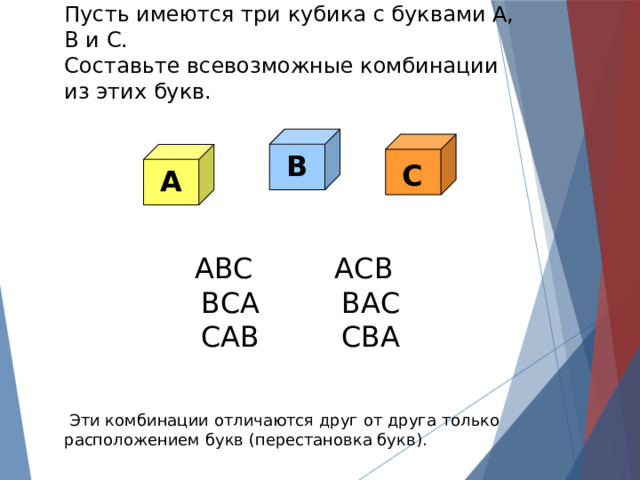
Пусть имеются три кубика с буквами А, В и С.

Составьте всевозможные комбинации из этих букв.

ABC АСВ

ВСА ВАС

CAB CBA

Эти комбинации отличаются друг от друга только расположением букв (перестановка букв).

В

С

А

Перестановки

Определение

Перестановки - это комбинации, составленные из одних и тех же элементов и отличающиеся порядком их следования.

Число перестановок из n элементов обозначают

Читают «P из n».

Число всевозможных перестановок из n элементов вычисляется по формуле :

P n = n!

При перестановке число объектов остается неизменными,

меняется только их порядок

13

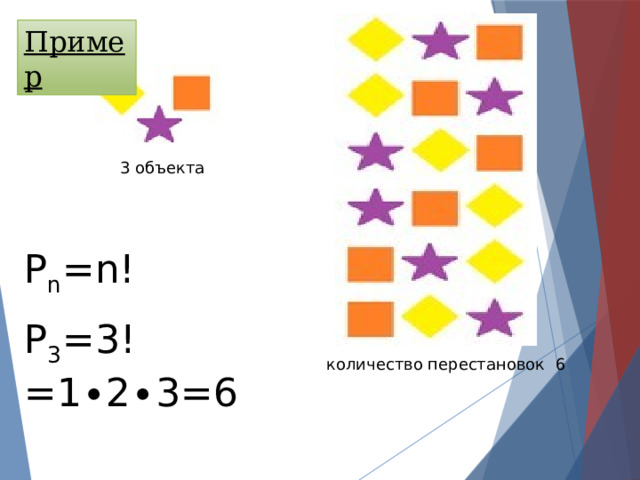
Пример

3 объекта

Р n =n!

Р 3 =3!=1 ∙2∙3=6

количество перестановок 6

Задача 1. В турнире участвуют семь команд. Сколько вариантов распределения мест между ними возможно? 

Р 7 =7!=1*2*3*4*5*6*7=5040

Ответ: 5040

Задача 2. Сколькими способами могут разместиться за круглым

столом 10 человек? 

Р 10  =10! = = 1*2*3*4*5*6*7*8*9*10 = 3628800 

Ответ: 3628800

Задача 3.

В среду в 9 классе 6 уроков: алгебра, русский язык, черчение, биология, химия, обществознание.

а) Сколько вариантов расписания можно составить на среду?

Р 6 =6!=1*2*3*4*5*6=720

б) Сколько вариантов расписания можно составить на среду так, чтобы алгебра была первой?

Р 5 =5!=1*2*3*4*5=120

в) Сколько вариантов расписания можно составить на среду так, чтобы биология и химия не стояли рядом?

2*Р 5 =2*5!=2*(1*2*3*4*5)=2*120=240

Размещения

Пусть имеется n различных объектов. Будем выбирать из них m объектов и переставлять всеми возможными способами между собой .

Получившиеся комбинации называются размещениями из n объектов по m , а их число равно:

Определение

Комбинации, составленные из m элементов, взятых из n элементов, и отличающиеся друг от друга либо составом, либо порядком расположения элементов, называются размещениями из n элементов по m ( 0 ≤n ).

Формула размещения:

При размещениях меняется и состав выбранных объектов, и их порядок.

Читается:

размещение из n элементов по m элементов. А первая буква французского слова arrangement : «размещение», «приведение в порядок»

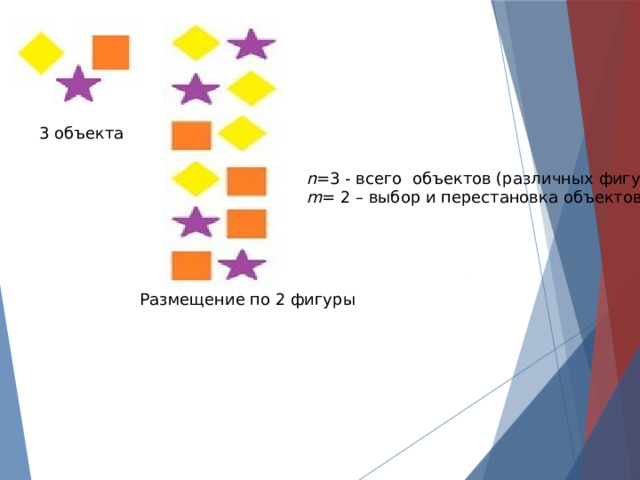
3 объекта

n =3 - всего объектов (различных фигур)

m = 2 – выбор и перестановка объектов

Размещение по 2 фигуры

Задача1. Сколькими способами можно расставить 5 томов на книжной полке, если выбирать их из имеющихся в наличии семи книг?

Ответ: 2520 способов

• Вычислить:

Задача 2. Найти количество трехзначных чисел с неповторяющимися цифрами, которые можно составить из цифр: 0,1, 2, 3, 4, 5.

Сочетания

3 объекта

Пусть имеется n различных объектов. Будем выбирать из них m объектов все возможными способами

Получившиеся комбинации называются сочетаниями из n объектов по m ,

В сочетаниях меняется состав выбранных объектов, но порядок не важен

05/22/2023

Определение

• Сочетанием из п элементов по m называют любое множество, составленное из m элементов, выбранных из п элементов

В отличии от размещений в сочетаниях не имеет значение порядок элементов . Два сочетания отличаются друг от друга хотя бы одним элементом

13

13

Задача 1: Сколькими способами можно распределить три путевки в один санаторий между пятью желающими? 

Так как путевки предоставлены в один санаторий, то варианты распределения отличаются друг от друга хотя бы одним желающим. Поэтому число способов распределения

Ответ: 10 способов.

Задача 2:

Группу из 20 студентов следует рассадить в аудитории по 2 человека за каждой партой. Порядок их размещения не имеет значения. Определить количество возможных вариантов сочетаний.

Ответ: 190

Задача 3: В цехе работают 12 человек: 5 женщин и 7 мужчин. Сколькими способами можно сформировать бригаду из 7 человек, чтобы в ней было 3 женщины? 

Из пяти женщин необходимо выбирать по три, поэтому число способов отбора      .

Так как требуется отобрать четырех мужчин из семи,

то число способов отбора мужчин      

Ответ: 350

Ответим на вопросы

• Что изучает комбинаторика ?
• Кем был введен в математический обиход термин « комбинаторика» ?
• Какие способы решения комбинаторных задач рассмотрели на уроке?
• Что означает запись n! ?
• Найдите значение выражения 4!.
• Что называется перестановкой из n элементов?
• Что называют размещением из n по m элементов?

8) Чем сочетания отличаются от размещения из n по m элементов?

Закончи предложение:

• Сегодня на уроке я запомнила……………..
• Я научилась……………………………………
• Я поняла……………………………………......
• У меня не получилось………………………
• Мне бы хотелось…………………………….
• Я справлюсь с домашней работой………...