Конспект урока "Комбинаторные задачи"

Конспект урока

КОМБИНАТОРНЫЕ ЗАДАЧИ

Выполнила: Беляева Ольга Петровна

учитель математики МОУ лицея № 28 имени Н.А.Рябова города Тамбова

Форма занятия: комбинированный урок

Цели урока:

• Образовательная - Обучать решению задач по комбинаторике

• Развивающая Способствовать развитию:

- умения воспроизводить информацию, кратко излагать свои мысли,

- логического мышления,

- умения работать со справочной информацией,

- умения работать в команде,

- умения работать самостоятельно

• Воспитательная

Способствовать формированию:

- интереса к предмету,

- ответственности, аккуратности,

- культуры поведения, общения

Задачи урока:

- отработать умения решать комбинаторные задачи,

- проверить понимание материала, изученного на лекции и практическом занятии

ТСО:

Технические средства:

Компьютер, проекционная аппаратура

Программные средства:

Microsoft Word, Microsoft Power Point

Перечень вопросов, изучаемых в данной теме:

правило суммы,

правило произведения,

Общие рекомендации к проведению данного урока:

Отличительные особенности данного урока:

Используется мультимедийная презентация, в которой сохранена структура занятия. В презентации имеется приложение, состоящее из исторической справки и шпаргалки для студентов, испытывающих затруднения при решении задач.

Ход урока

1. Организационный момент, постановка целей и задач урока

2. Активизация познавательной деятельности

3. Изложение нового материала

При решении многих практических задач приходится выбирать из некоторого множества объектов элементы, обладающие тем или иным свойствам, располагать эти элементы в определенном порядке, подсчитывать число выбранных элементов. Например, мастеру приходится распределять различные виды работ между рабочими, агроному размещать сельскохозяйственные культуры на нескольких полях и т.д. В этих задачах речь идет о тех или иных комбинациях объектов и, поэтому, называют их комбинаторными задачами, а раздел математики, в котором рассматриваются подобные задачи, называют комбинаторикой. Слово «комбинаторика» происходит от латинского слова combinare, которое означает «соединять, сочетать».

Рассмотрим некоторые комбинаторные задачи.

Пример 1. У Ирины пять подруг: Вера, Зоя, Марина, Полина, Светлана. Она решила двух из них пригласить в кино. Укажите все возможные варианты выбора подруг. Сколько таких вариантов?

Решение: Для решения задачи воспользуемся способом рассуждений, который называется перебор возможных вариантов. Для каждой из девочек будем писать первые буквы имен и составим все пары, в которые

• входит Вера: ВЗ, ВМ, ВП, ВС;

• входит Зоя, но не входит Вера: ЗМ, ЗП, ЗС;

• входит Марина, но не входят Вера и Зоя: МП, МС;

• входит Полина, но не входят Вера, Зоя, Марина: ПС

Других вариантов для составления пар нет. Подсчитывая результат, получаем, что у Ирины существует 10 вариантов выбора пары подруг для похода в кино.

Ответ: ВЗ, ВМ, ВП, ВС, ЗМ, ЗП, ЗС, МП, МС, ПС. 10 вариантов.

Пример 2. В кафе предлагают два первых блюда: борщ, рассольник; три вторых блюда: пельмени, гуляш, сосиски; два третьих блюда: компот, чай. Сколько возможных обедов из первого второго и третьего блюда может заказать посетитель?

Решение: Для перебора всех случаев построим схему, которую называют дерево возможных вариантов. Для краткости будем писать первые буквы указанных блюд.

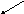
1 блюда: Б Р

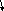
2 блюда: П Г С П Г С

3 блюда: К Ч К Ч К Ч К Ч К Ч К Ч

Таким образом, всего можно заказать 12 различных обедов.

Ответ: 12.

Перебор вариантов (пример 1) или дерево возможных вариантов (пример2) удобно использовать для небольшого числа вариантов. В противном случае при различных подсчетах рациональнее использовать правила суммы и произведения.

Правило произведения: если элемент а можно выбрать m различными способами, а для каждого из этих способов некоторый элемент b можно выбрать п способами, то выбор «а и b» можно сделать mn способами.

Например, в группе из 8 учащихся выбирают старосту и профорга. Существует 8 способов выбора старосты. Профоргом может быть каждый из 7 оставшихся человек. Поэтому существует 87=56 способов выбора старосты и профорга.

Рассмотрим решение примера 2 с использованием правила произведения: выбор 1-го блюда можно осуществить 2 способами, 2-го блюда 3 способами, 3-го блюда 2 способами. Весь обед можно составить 232=12 способами. Это решение показывает, что правило умножения можно сформулировать в более общем виде:

Если нужно сформировать комбинацию из k элементов и при этом первый элемент в комбинации можно выбрать п₁ способами, после чего второй элемент можно выбрать п₂ способами, затем третий элемент – п₃ способами из оставшихся и т.д., то число таких комбинаций будет равно произведению п₁п₂п₃…п_k.

Пример 3. Сколько четырехзначных чисел можно составить из цифр 0,1,2,3,4,5, если:

а)ни одна цифра не повторяется больше одного раза в записи числа;

б)цифры в записи числа могут повторяться;

в)цифры могут повторяться в записи числа, но число должно быть нечетным.

Решение.

а) Первой цифрой при этом может быть любая из 5 цифр 1,2,3,4,5 (0 не может быть первой цифрой, потому что в таком случае число не четырехзначное). Если первая цифра выбрана, то вторая может быть выбрана 5 способами, третья — 4 способами, четвертая — 3 способами. Согласно правилу произведения общее число способов равно 5•5•4•3=300.

б) Для первой цифры имеем 5 возможностей (1,2,3,4,5), для каждой из следующих цифр — 6 возможностей (0,1,2,3,4,5). Следовательно, общее количество чисел равно 5•6•6•6=1080.

в) Первой цифрой может быть одна из 5 цифр 1,2,3,4,5, а последней 1,3,5. Следовательно, общее количество чисел равно 5•6•6•3=540.

Правило суммы: если элемент а можно выбрать m способами, а элемент b – n способами, причем любой выбор элемента а отличен от любого выбора элемента b, то выбор «а или b» можно сделать m+n способами.

Например, на книжной полке стоят 20 книг по алгебре, 7 книг по геометрии. Книгу по математике (алгебре или геометрии) можно выбрать 20+7=27 способами.

Но бывают задачи, в которых после выбора одного из объектов в качестве первого элемента нельзя однозначно сказать, сколькими способами можно выбрать второй элемент – это зависит от того, какой объект был выбран первым. В этом случае приходится разбивать все перечисляемые комбинации на попарно непересекающиеся группы, подсчитывать число элементов в каждой группе и складывать получившиеся ответы.

Пример 4. Определите количество трехзначных чисел, которые можно составить из цифр 1,2,3,4,5, так, чтобы каждая предыдущая цифра была меньше последующей.

Решение: На первое место можно выбрать цифру тремя способами. Рассмотрим каждый из случаев:

Первая цифра – 1. Вторая цифра – 2. Третью цифру выбираем 3 способами

Вторая цифра – 3. Третью цифру выбираем 2 способами

Вторая цифра – 4. Третью цифру выбираем 1 способом.

Получаем, что существует 6 трехзначных чисел, начинающихся с цифры 1 и удовлетворяющих условию задачи.

Первая цифра – 2. Вторая цифра – 3. Третью цифру выбираем 2 способами.

Вторая цифра – 4. Третью цифру выбираем 1 способом.

Существует 3 способа построения трехзначных чисел, начинающихся с 2 и удовлетворяющих условию задачи. И, наконец, существует единственное число 345, начинающееся с цифры 3.

В итоге, всего существует 6+3+1=10 таких чисел.

1. Решение упражнений на усвоение теоретического материала и закрепление навыков решения задач (фронтальное обсуждение способов решения задач, их достоинства и недостатки; решение записывается в тетрадях и на доске).

1. й

1. Заключительный этап урока

1. самостоятельная работа или тест

2. подведение итогов