ПЛАН-КОНСПЕКТ УРОКА
Тема «Параллелепипед. Прямоугольный параллелепипед. Куб»
Цели урока:
Рассмотреть понятие параллелепипеда и его видов;
закрепить знания о свойствах при решении задач обязательного уровня;
Обучающие:
рассмотреть понятие параллелепипеда и его видов;
доказать свойства параллелепипеда;
дать определение прямоугольного параллелепипеда и доказать его свойство диагоналей;
рассмотреть примеры применения свойств в решении задач;
Развивающие:
способствовать развитию внимания, умений сравнивать, классифицировать, выделять главное;
переносить знания в новую ситуацию;
анализировать условие задачи;
логического мышления, математической речи;
Воспитательные:
содействовать воспитанию графической культуры;
содействовать воспитанию культуры речи учащихся, умения общаться.
Тип урока: изучение нового материала.
Оборудование: учебник А. В. Погорелова «Геометрия 10-11», модели геометрических тел, раздаточный материал: таблица сравнения параллелепипедов.
План урока:
Организационный момент
Актуализация знаний
Изучение нового материала
Первичное закрепление знаний
Подведение итогов
Домашнее задание
Ход урока:
Организационный момент
Проверка готовности помещения к уроку, приветствие учеников, проверка посещаемости.
Актуализация знаний
На предыдущих уроках мы знакомились с многогранниками – представителями геометрических тел, а именно с призмой. Сегодня продолжаем изучение призм, подробнее изучим знакомый из школьного курса математики параллелепипед, предварительно вспомнив главное о призме.
Что называют призмой? (Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников).
Среди представленных моделей выберите призмы (Учащиеся выбирают призмы, оставляя пирамиды и тела вращения).
Показываю учащимся модель призмы и прошу рассказать как изобразить эту призму на листе в тетради.
Расскажите алгоритм построения призмы? (В соответствии с правилами параллельного проектирования изображение призмы строится следующим образом. Сначала строится одно из оснований Р. Это будет некоторый плоский многоугольник. Затем из вершин многоугольника Р проводятся боковые ребра призмы в виде параллельных отрезков равной длины. Концы этих отрезков соединяются, и получается другое основание призмы. Невидимые ребра проводятся штриховыми линиями).
Разделите призмы на две группы, предварительно выбрав основание классификации Обсудив, что можно выбрать в качестве основания для классификации, выбираем многоугольник, лежащий в основании. Учащиеся выбирают группу моделей, в основании которых лежит параллелограмм, ромб, прямоугольник, квадрат).
На какие еще группы можно еще разделить выбранные модели? ( Прямые и наклонные)
Изучение нового материала
Перейдем к изучению новой темы: Параллелепипед. Прямоугольный параллелепипед. Куб.
Разделив модели, мы получили различные параллелепипеды.
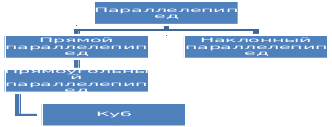
Сформулируем определение параллелепипеда.
Параллелепипед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них — параллелограмм.
Сформулируем определение прямоугольного параллелепипеда.
Через прямой параллелепипед: Прямоугольный параллелепипед – это прямой параллелепипед, у которого в основании прямоугольник
Через параллелепипед: Прямоугольный параллелепипед – это параллелепипед, который является прямым, а в основании лежит прямоугольник
Через призму: Прямоугольный параллелепипед – это четырехугольная призма, которая является прямой, в основании которой лежит прямоугольник.
Дадим различные определения куба.
Через прямоугольный параллелепипед: Куб – это прямоугольный параллелепипед с равными ребрами.
Через параллелепипед: Куб - это параллелепипед, у которого все грани квадраты.
Через призму: Куб – это четырехугольная призма с равными ребрами.
Ребята! При решении задач очень важно правильно истолковать условие задачи, а именно хорошо понимать, о каком параллелепипеде идет речь. Предлагаю заполнить такую сравнительную таблицу: самостоятельно( в парах) с последующей проверкой.
Сравнительная характеристика параллелепипеда и прямоугольного параллелепипеда:
|
| Параллелепипед | Прямоугольный параллелепипед |
| Вид | Прямой или наклонный | Всегда прямой |
| Основание | Параллелограмм, ромб, прямоугольник, квадрат | Прямоугольник или квадрат |
| Высота | Длина перпендикуляра между основаниями, либо длина бокового ребра | Длина перпендикуляра между основаниями, либо длина бокового ребра |
Переходим к рассмотрению основных свойств параллелепипеда.
У параллелепипеда противолежащие грани параллельны и равны.
параллелепипеда противолежащие грани параллельны и равны.
Дано: ABCDA1B1C1D1 – параллелепипед, основание - параллелограмм
Доказать: ADD1A1=CBB1C1, ADD1A1||CBB1C1
Предложить провести доказательство учащимся. Если есть варианты доказательств, то заслушать их. Если полных версий нет, то проводится беседа, после чего излагается полное доказательство.
Д оказательство: Рассмотрим две противолежащие грани параллелепипеда. Так как все грани параллелограммы, то AD||BC, AA1||DD1, следовательно, плоскости граней параллельны. Так как грани параллелограммы, то AB, A1B1, D1C1, DC параллельны и равны, значит грани равны.
оказательство: Рассмотрим две противолежащие грани параллелепипеда. Так как все грани параллелограммы, то AD||BC, AA1||DD1, следовательно, плоскости граней параллельны. Так как грани параллелограммы, то AB, A1B1, D1C1, DC параллельны и равны, значит грани равны.
2.Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Предложить провести доказательство учащимся. Если есть варианты доказательств, то заслушать их. Если полных версий нет, то проводится беседа, после чего излагается полное доказательство.
Учащиеся делаются рисунок в тетради, один ученик выходит к доске. Ученики строят параллелепипед. Далее проводятся две пересекающиеся диагонали параллелепипеда. Раз прямые пересеклись, значит, они задают плоскость (две пересекающиеся прямые задают плоскость). Достраиваем рисунок до сечения. В сечении получился параллелограмм. А в параллелограмме диагонали точкой пересечения делятся пополам.
Т еперь мы рассмотрим теорему, справедливую только для прямоугольного параллелепипеда.
еперь мы рассмотрим теорему, справедливую только для прямоугольного параллелепипеда.
Теорема. В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.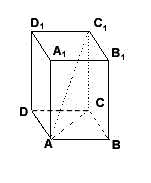
Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; основание – прямоугольник
x, y, z - три его измерения.
Доказать:
Квадрат диагонали параллелепипеда равен сумме квадратов трех его измерений
(AC12=CC12+AB2+BC2)
П редложить провести доказательство учащимся. Если есть варианты доказательств, то заслушать их. Если полных версий нет, то проводится беседа, после чего излагается полное доказательство. Доказательство:
редложить провести доказательство учащимся. Если есть варианты доказательств, то заслушать их. Если полных версий нет, то проводится беседа, после чего излагается полное доказательство. Доказательство:
1) AB, CB, CC1 - ребра. Их длины являются линейными размерами параллелепипеда. AB = x, CC1 = y, BC = z
2) Рассмотрим DAC1C: ÐC1CA = 90° т.к. СC1^ABCD, Þ CC1^ ACÌ(ABCD)
По теореме Пифагора: AC12 = AC2 + AC12
3) Рассмотрим DABC: ÐCBA = 90° (ABCD - прямоугольный по условию )
По теореме Пифагора: AC2 = BС2 + AB2
AC12=CC12+AB2+BC2
Сформулировать теорему для куба: d2=3a2.
Первичное закрепление знаний
А сейчас переходим к решению задач по теме «Параллелепипед».
Задача, на применение свойств параллелепипеда.
№ 26. У параллелепипеда три грани имеют площади 1м2, 2 м2, 3м2. Чему равна полная поверхность параллелепипеда?
Решение:
У параллелепипеда противоположные грани равны, а значит, имеют равные площади. Так что данный параллелепипед имеет две грани с площадью 1м2, две грани с площадью 2м2 и две грани с площадью по 3м2. Так что площадь полной поверхности S=2*(1+2+3)=12(м2)
Ответ: 12 м2
№29. В прямом параллелепипеде стороны оснований 6 м и 8 м образуют угол 30о, боковое ребро равно 5м. Найдите полную поверхность этого параллелепипеда.
Решение:
Полная поверхность прямого параллелепипеда равна Sполн=2Sосн+Sбок
Площадь параллелограмма ABCD , являющегося основанием , равна Sосн=AB*AD*sin30o=6*8*1/2=24
Площадь боковой поверхности равна Sбок=p*l=2(AB+BC)AA1=2*(6+8)*5=140
Так что Sполн=2*24+140=188
Ответ:188
Подведение итогов
Понятия параллелепипед и прямоугольный параллелепипед вам известны из предыдущего курса математики и из жизненной практики. Какие их свойства вам были уже известны (без доказательства), а о каких вы узнали впервые? (Учащиеся формулируют свойства граней, а в качестве нового формулируют свойство диагонали прямоугольного параллелепипеда).
Давайте с вами составим синквейн на тему «Параллелепипед» как итог нашего урока.
Пример:
Параллелепипед
Прямоугольный, прямой.
Строить, вычислять, сравнивать.
Я узнал о параллелепипеде.
Призма
Домашнее задание
п.45, п.46, задачи: 30,37.







 параллелепипеда противолежащие грани параллельны и равны.
параллелепипеда противолежащие грани параллельны и равны. оказательство: Рассмотрим две противолежащие грани параллелепипеда. Так как все грани параллелограммы, то AD||BC, AA1||DD1, следовательно, плоскости граней параллельны. Так как грани параллелограммы, то AB, A1B1, D1C1, DC параллельны и равны, значит грани равны.
оказательство: Рассмотрим две противолежащие грани параллелепипеда. Так как все грани параллелограммы, то AD||BC, AA1||DD1, следовательно, плоскости граней параллельны. Так как грани параллелограммы, то AB, A1B1, D1C1, DC параллельны и равны, значит грани равны. 










