Тюнева Надежда Васильевна
учитель математики,
МАОУ «Светлинская СОШ №2»
п. Светлый, Светлинский район,
Оренбургская область.
Название предмета: Геометрия
Класс 8
УМК: Учебник Геометрия 7 – 9, Л.С.Атанасян и др., М., Просвещение 2015,
Уровень обучения: базовый
Тема урока: Решение задач на вычисление площадей
Общее количество часов, отведенное на изучение темы: 14
Место урока в системе уроков по теме: восьмой( 22)
Цели урока:
- закрепить теоретический материал по теме «Площадь»;
- познакомить учащихся с методами решения задач по теме «Площадь многоугольников»;
- совершенствовать навыки решения задач по теме «Площадь параллелограмма, треугольника, ромба, трапеции»
Задачи урока:
Формировать устойчивые знания о площадях параллелограмма, треугольника ромба, трапеции ;
Развивать навыки применение формул при решении задач
Воспитывать творческую самостоятельность учащихся.
Планируемые результаты:
- Умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин, умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем, - умение видеть различные стратегии решения задач, умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера
Техническое обеспечение урока: учебник, компьютер, мультимедеопроектор,
Литература:
1. Атанасян, Л. С. Изучение геометрии в 7, 8, 9 классах : метод. рекомендации к учебнику : книга для учителя / Л. С. Атанасян [и др.]. – Изд. 6-е. – М. : Просвещение, 2003.
2. Арутюнян, Е. Б. Математические диктанты для 5–9 классов : книга для учителя / Е. Б. Арутюнян [и др.]. – М. : Просвещение, 1991.
3. Березина, Л. Ю. Геометрия в 7–9 классах : пособие для учителя / Л. Ю. Березина [и др.]. – М. : Просвещение, 1990.
4. Гайштут, А. Г. Планиметрия : задачник к школьному курсу / А. Г. Гайштут, Г. Н. Литвиненко. – М. : АСТ-Пресс : Магистр-S, 1998.
5. Зив, Б. Г. Дидактические материалы по геометрии для 8 класса / Б. Г. Зив, В. М. Мейлер. – М. : Просвещение, 1992.
6. Кабалевский, Ю. Д. Самостоятельная работа учащихся в процессе обучения математике : книга для учителя : из опыта работы / Ю. Д. Кабалевский. – М. : Просвещение, 1988.
7. Полонский, В. Б. Геометрия : задачник к школьному курсу / В. Б. Полонский [и др.]. – М. : Аст-Пресс : магистр-S, 1998.
8. Саврасова, С. М. Упражнения по планиметрии на готовых чертежах : пособие для учителя / С. М. Саврасова, Г. А. Ястребинецкий. – М. : Просвещение, 1987.
Содержание урока
Ход урока
I. Организационный момент
II. Проверка домашнего задания.
1. Обсудить решение домашних задач.
2. Выполнить задания (устно):
| 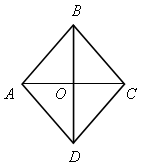
| 1) АВСD – ромб. ВD = 18 см, АС = 10 см. Найти: SАВСD. |
| 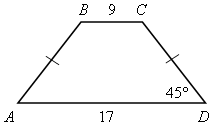
| 2) АВСD – равнобокая трапеция. Найти: SАВСD. |
III. Решение задач.
№ 477.
Решение
| 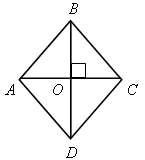
| Пусть АС = х, тогда ВD = 1,5х, SАВСD = 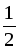 АС · ВD, АС · ВD, 27 = 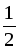 x ∙ x ∙ 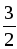 x; 27 = x; 27 = 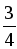 x2. x2. х2 = 36; х = 6. АС = 6 см, ВD = 9 см. |
№ 478.
Решение
| 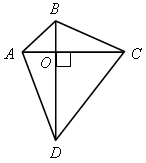
| 1) SАВСD = SАВС + SАDС. 2) ВО – высота  АВС, а DО высота АВС, а DО высота  АDС, поэтому SАВС = АDС, поэтому SАВС = 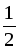 АС · ВО, АС · ВО, SАDС = 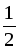 АС · ОD. АС · ОD. Следовательно |
SАВСD = 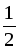 АС · ВО +
АС · ВО + 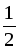 АС · ОD =
АС · ОD = 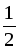 АС (ВО + ОD);
АС (ВО + ОD);
SАВСD = 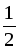 АС · ВD.
АС · ВD.
Задача 1. В трапеции АВСD АD – большее основание, 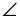 D = 60. Биссектрисы углов С и D пересекаются в точке О, ОD = а, ВС = b, АD = с. Найдите площадь трапеции.
D = 60. Биссектрисы углов С и D пересекаются в точке О, ОD = а, ВС = b, АD = с. Найдите площадь трапеции.
Решение
| 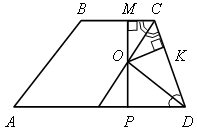
| 1) Проведем ОМ 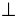 ВС, ОK ВС, ОK 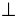 СD и ОР СD и ОР 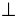 АD. АD. 2) Из равенства прямоугольных треугольников МСО и KСО следует, что ОМ = ОK. 3) из равенства прямоугольных треугольников ОРD и ОKD следует, что ОK = ОР. |
4) Имеем ОМ = ОР = ОK.
5) В прямоугольном треугольнике KОD катет ОK лежит против угла в 30 и равен половине гипотенузы, то есть ОK = 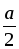 .
.
6) SАВСD = 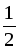 (ВС · АD) · МР; SАВСD =
(ВС · АD) · МР; SАВСD = 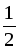 (b + с).
(b + с).
Задача 2. Четырехугольник, у которого диагонали пересекаются под прямым углом, имеет площадь 250 см2. Найдите его диагонали, если известно, что одна больше другой в 5 раз.
Ответ: 10 и 50 см.
IV. Рефлексия.
| 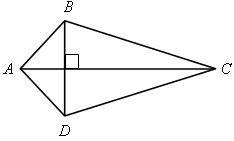
| SАВСD = 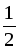 d1 · d2 – площадь d1 · d2 – площадь
четырехугольника, где d1 и d2 –
диагонали. |
V.Домашнее задание: вопросы 1–7, с. 133–134; №№ 476 (б), 470, 466.























