Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа – детский сад № 37 имени партизана-подпольщика И.Г. Генова» муниципального образования городской округ Симферополь Республики Крым
Методическая разработка урока
По геометрии в 10 классе на тему: «Призма»
Подготовила и провела
учитель математики
Морозова В.А.
2022/2023 учебный год
Урок № 110
Дата проведения: 14.02.23
Класс: 10-А.
Тема урока: «Призма».
Тип урока: изучение и первичное закрепление новых знаний.
Оборудование: компьютер, мультимедийный проектор, раздаточный материал, презентация к уроку.
Цель урока:
Обучающая: Сформировать представление о призме, её элементах; виды призм; вычисление площади поверхности призмы.
Развивающая: активизировать навыки познавательной активности, образного и логического мышления учащихся; развивать навыки самостоятельной работы учащихся.
Воспитательная: воспитывать положительную мотивацию к изучению математики, умения договариваться, слушать и слышать другого, принимать решения.
Форма работы: групповая, фронтальная.
Оборудование: модели фигур, компьютер, раздаточный материал
План урока
-
Организационный момент. Актуализация знаний (5 мин)
-
Изучение нового материала (15 мин)
-
Закрепление изученного материала (20 мин)
-
Домашнее задание (2 мин)
-
Подведение урока. Рефлексия (3 мин)
Ход урока.
1. Организационный момент. Актуализация знаний.
Великий архитектор Ле Корбюзье говорил: «Окружающий нас мир – это мир геометрии чистой, истинной, безупречной в наших глазах. Все вокруг – геометрия». Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями человека. Мы продолжаем знакомиться с многогранниками.
Но прежде ответьте на вопросы:
-объясните, что такое многогранник, поверхность многогранника
-назовите известные вам многогранники
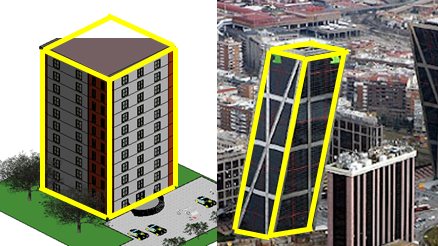
 Ребята, посмотрите на картинку (рис.1). Все это здания архитектуры, и все они имеют форму многогранников. Все это призмы. Призма – один из видов многогранников.
Ребята, посмотрите на картинку (рис.1). Все это здания архитектуры, и все они имеют форму многогранников. Все это призмы. Призма – один из видов многогранников.
2. Изучение нового материала. Фронтальная работа с классом.
Используя изображение, ответьте на вопросы:
| 
| Сколько оснований у призмы? |
| Что лежит в основании призмы? |
| В каких плоскостях лежат основания призмы? |
| Какими многоугольниками являются все грани призмы? |
| Определение | Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой |
|
| Какими отрезками являются боковые ребра призмы? |
| Определение | Диагональ призмы — это отрезок, который соединяет две вершины, не принадлежащие одной грани. |
| Определение | Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. |
Обратимся к рис.1. Какие многоугольники лежат в основании каждой призмы? Название призмы связывают с числом углов в многоугольнике основания. Например, на рис.1 изображены треугольная, четырехугольная и шестиугольная призмы.
| 
| Сравните призмы. Призмы делятся на: |
| Прямые | Наклонные |
| Боковые ребра перпендикулярны основанию. Боковые грани – прямоугольники. | Боковые ребра не перпендикулярны основанию. Боковые грани – параллелограммы. |
|
| Правильная |
| 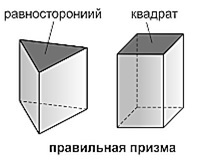
| Прямая призма называется правильной, если в ее основании лежит правильный многоугольники. |
Теорема: Площадь боковой поверхности прямой призмы равна произведению площади основания на её высоту. Sбок = Росн · h
Площадь полной поверхности призмы равна сумме площади боковой поверхности и удвоенной площади основания.
Sполн= Sбок+2Sосн,
3. Закрепление изученного материала.
1) Среди многогранников выбери призмы и определи их вид (устно)
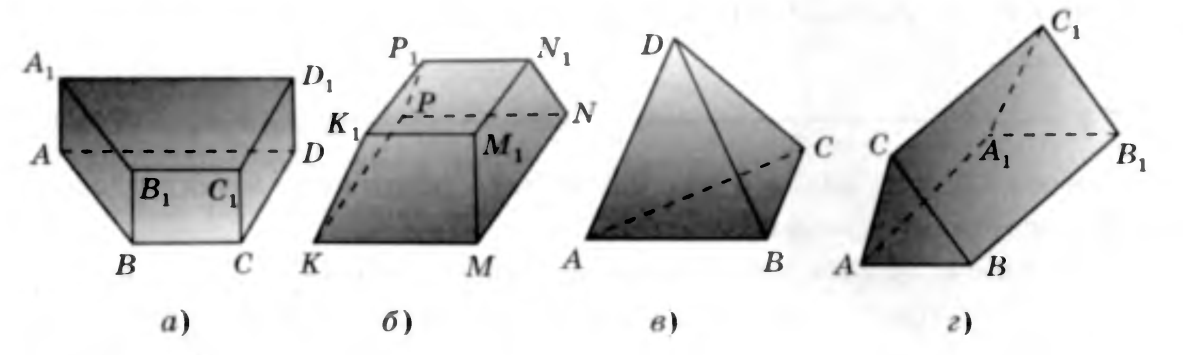
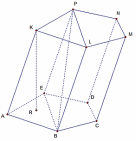
2) Используя рисунок, заполните пропуски в тексте. Вершины____________________________
Боковые ребра_______________________
Диагональ призмы____________________
Высота______________________________
ВЕ – это ____________________________
Кол-во боковых граней _______________
АВСDEKPNML – … призма
3) В основании наклонной призмы лежит квадрат со стороной 5см. Найдите сумму ребер призмы, если боковое ребро равно 12см.
4) Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
4.Домашнее задание. По карточкам
5. Подведение итого. Рефлексия
Подведем итоги нашей работы. Рефлексия.
Что нового вы сегодня узнали?
Закончить фразу:
На уроке очень хорошо работали….







 Ребята, посмотрите на картинку (рис.1). Все это здания архитектуры, и все они имеют форму многогранников. Все это призмы. Призма – один из видов многогранников.
Ребята, посмотрите на картинку (рис.1). Все это здания архитектуры, и все они имеют форму многогранников. Все это призмы. Призма – один из видов многогранников. 






















