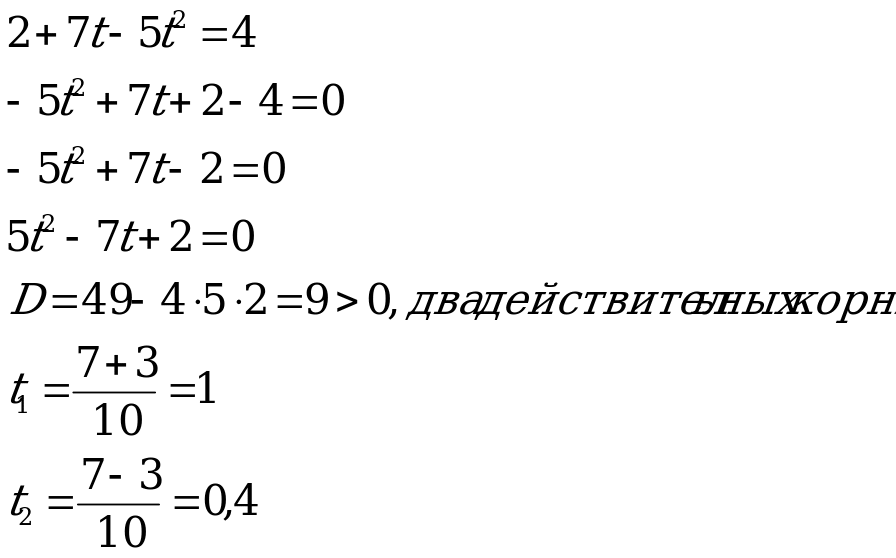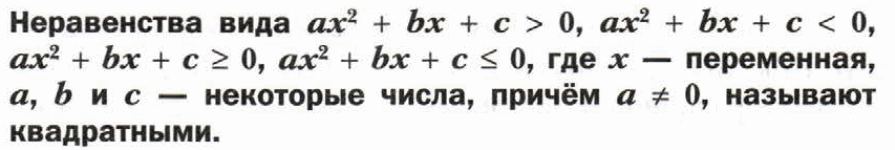Конспект урока "Решение квадратных неравенств"

Конспект урока 9 класс по теме « Решение квадратных неравенств.»

1. Орг. момент. Продолжить урок хотелось бы фразеологизмом «Камня на камне не оставим!». Так говорят, когда хотят что-либо разрушить или уничтожить до основания, до состояния пыли. Как это связано с уроком математики, спросите вы? Камни будут символизировать преграды, препятствия, которые встретятся нам на пути, а вместе с ними и сомнения, и волнения. Постараемся устранить преграды и освободить дорогу, ведущую к достижению цели!

2. Чтобы настроится на математический лад, проведем небольшую устную разминку. Перед вами первые камни преткновения!

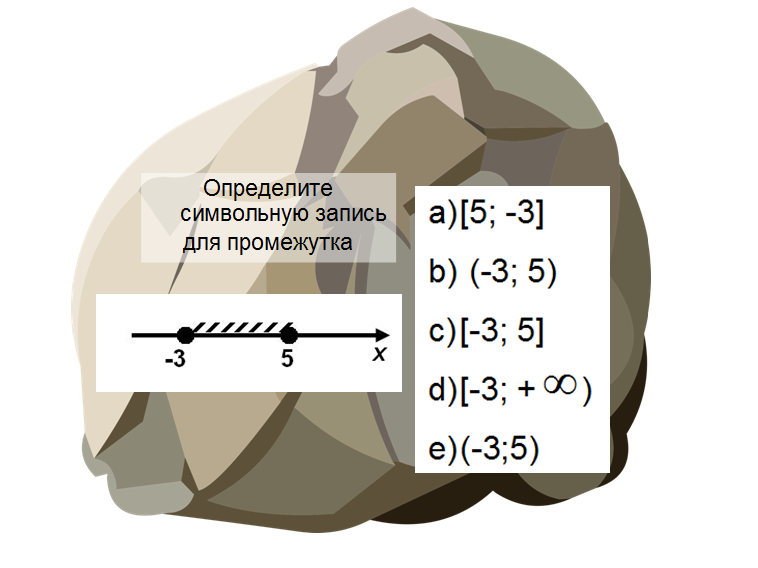
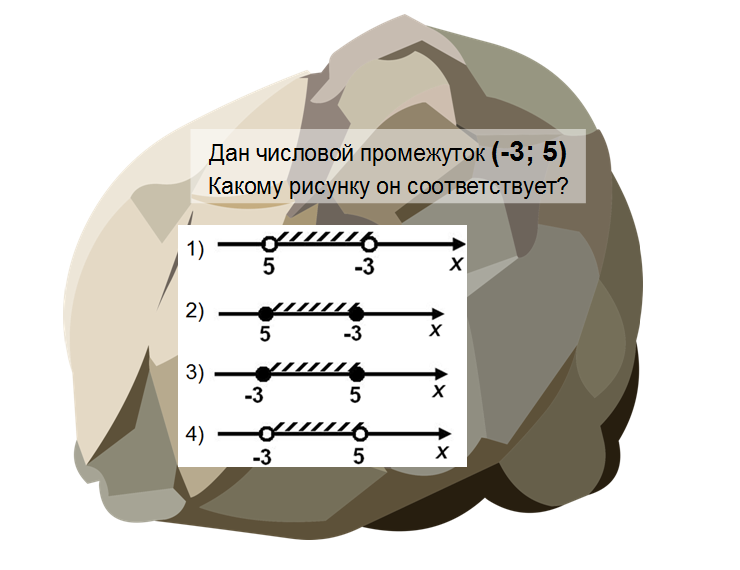
1. Что можно сделать с камнем? Первое, что приходит в голову – бросить. Проведем небольшой эксперимент с ним. Пусть один из камней будет подброшен вверх. Подбросьте! Понаблюдаем за его траекторией (вы, конечно, помните, что это линия в пространстве, вдоль которой движется тело). На какой из изученных вами графиков похожа траектория полета камня? Верно, на параболу. А парабола – это график какой функции? Верно, квадратичной.

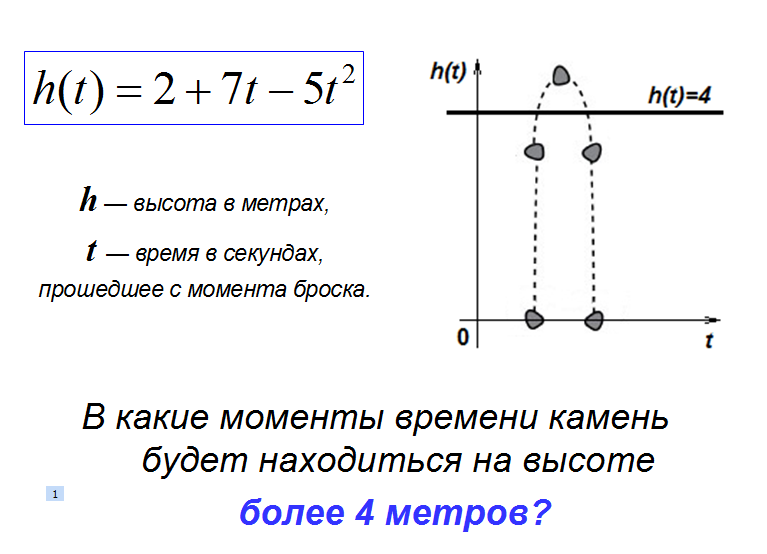
1. Предположим, высота над землей подброшенного вверх камня меняется по закону 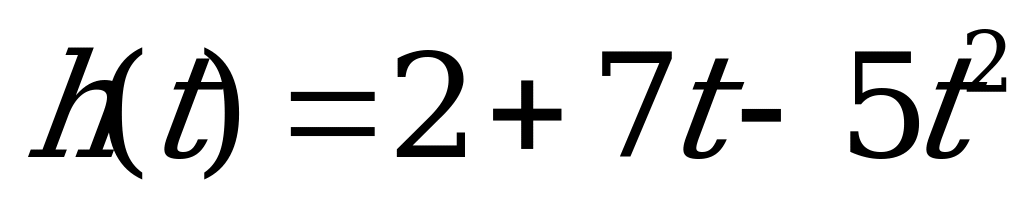, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Определим, в какие моменты времени камень будет находиться на высоте ровно 4 метра?

Схематический рисунок (комментарии)

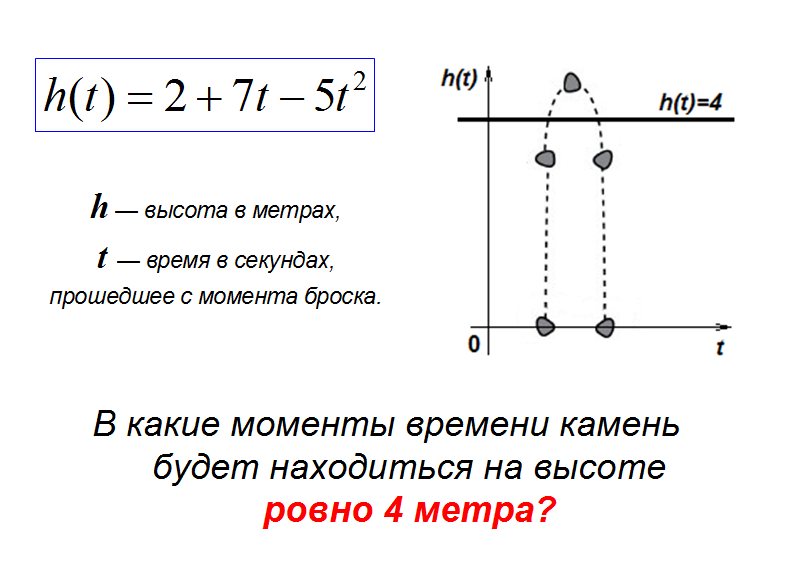
1. С одной стороны высота полета камня задана квадратным трехчленом, с другой стороны та же самая высота по условию задачи равна 4 метрам. Какую математическую модель мы можем составить? Верно, квадратное уравнение. А найдя его корни, мы отыщем те моменты времени t, которые нам интересны.

1. Решим наше уравнение из задачи с камнем (ребенок у доски).

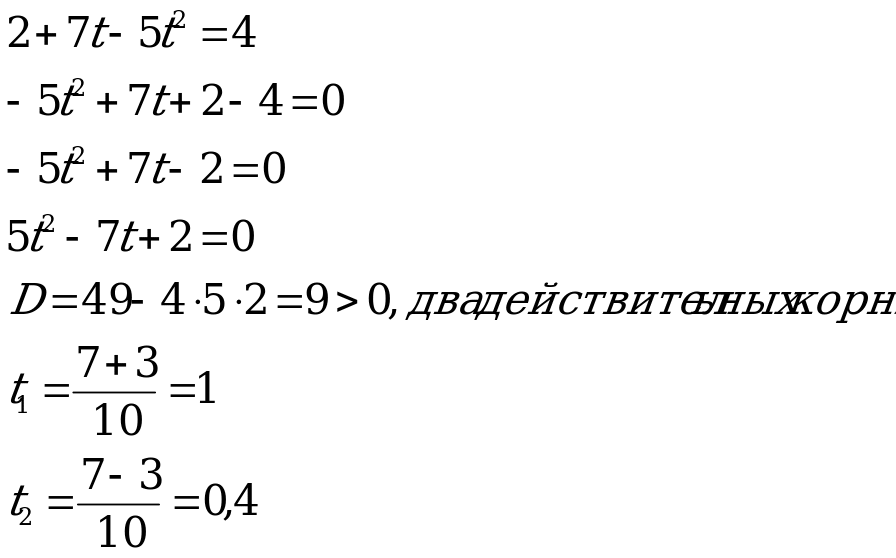
Вернемся к схематическому рисунку графика нашей функции, покажем на оси t найденные корни уравнения.

Ответ на вопрос задачи: на 0,4 секунды и на 1 секунде камень находился на высоте ровно 4 метра.

1. Вернемся к условию нашей задачи снова.

А что если нас попросили бы узнать, в какие моменты времени камень будет находиться на высоте более 4 метров?

Получаем другую модель реальной ситуации 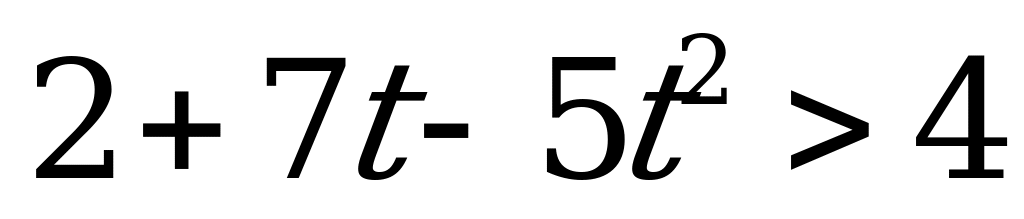. Знак равенства в этом случае изменяется на другой знак – знак неравенства.

Интуитивное решение по рисунку.

Функция принимает значения большие 4 на интервале (0,4; 1). Получается, ответом во второй части нашей задачи будет временной промежуток от 0,4с до 1с, не включая концы.

Запись: 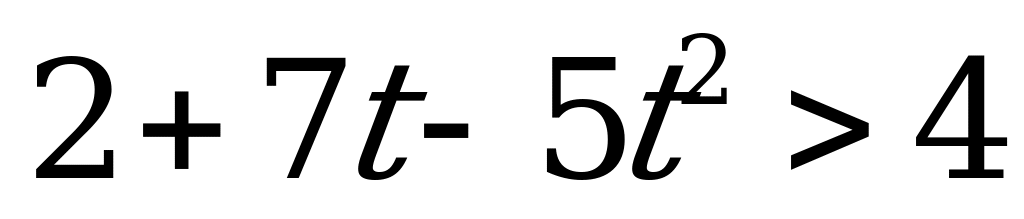, если t принадлежит (0,4; 1).

Скажите, пожалуйста, на каком еще уроке вам могла бы встретиться эта задача? На физике. Эту задачу решают при изучении темы «Тело, брошенное под углом к горизонту». Действительно, на каждом уроке мы используем знания, полученные ранее из других областей!

1. Мы решили только одну задачу, в которой пригодились знания о квадратичной функции. Все в природе строится на каких-либо закономерностях или правилах. Математика – это не только стройная система законов, теорем и задач, но и уникальное средство познания природы. Где в природе, в жизни еще можно встретить параболу?

2. Посмотрите, сколько разных ситуаций так или иначе будут задействовать квадратичную функцию!

Нам необходим единый алгоритм, который позволит нам успешно справиться с любым препятствием.

1. Итак, какова тема нашего урока? Какую цель мы поставим?

Запишите тему в тетради: «РЕШЕНИЕ КВАДРАТНЫХ НЕРАВЕНСТВ».

1. Переход к определению квадратного неравенства.

1. Устное задание на доске. Из предложенных неравенств выбрать квадратные. По цепочке передаем «камень» отвечающему.

1. Что значит решить неравенство? Найти множество его решений.

2. Может ли при решении квадратных неравенств нам помочь алгоритм решения квадратного уравнения?

3. Выработаем алгоритм решения квадратного неравенства (словесная форма представления алгоритма). Выработать вместе с детьми, вклеить в тетради стикеры с алгоритмом.

1. Итак, у нас есть алгоритм. Пора применить его на практике. Обратите внимание на раздаточный материал на ваших столах. Узнали? Действительно, это фрагмент варианта ОГЭ по математике, часть «Алгебра». Определите номера заданий, где только что изученный алгоритм нам сможет пригодиться. Дети находятся в поиске. Они определяют задания с квадратными неравенствами.

2. Решаем типичное задание из варианта ОГЭ, отработка алгоритма, например:

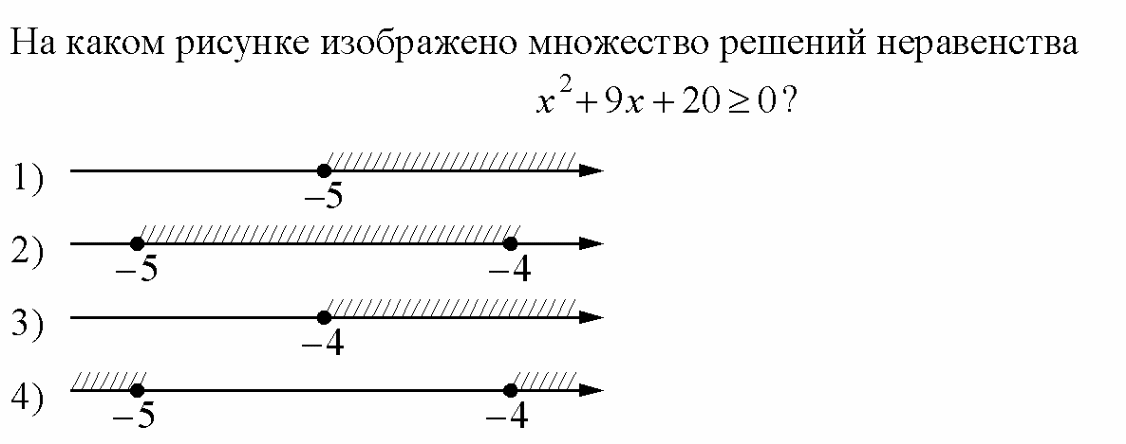
Внизу на слайде предусмотреть фрагмент (строку) из бланка ОГЭ, чтобы дети учились вписывать ответы правильно.

Достигли ли вы поставленной цели? Мы пока сделали первый, но уверенный шаг к освоению данной темы.

На ваших столах лежат камушки, у каждого – свой. У меня просьба: если вы считаете, что справились с трудностями этого занятия, то уходя, положите свой камушек в эту пиалу, если же нет, если у вас еще остались сомнения – то оставьте его на своем столе.

А я считаю, что вы просто молодцы! Все каменные преграды этого урока успешно преодолели! Хочу вам открыть один секрет: задача о камне мною была взята из варианта ЕГЭ для 11 класса. Теперь вы видите, что вам многое по силам! Перед вами свободная широкая дорога! Не нужно бояться трудностей, никакие камни вам не помеха! Желаю вам удачного пути! Благодарю за урок!

:

4х-15

27х³+19-5х

-16х-9

4х²- 3х-14 4*(-2)²-3*(-2)-14=8

3х-12≤ х²-5х