| Коло, вписане в трикутник Означення. | Коло називається вписаним у трикутник, якщо воно дотикається до всіх сторін трикутника.
| | Теорема. | В кожний трикутник можна вписати лише одне коло. Центром кола, вписаним в трикутник, є точка перетину його бісектрис, яка лежить усередині трикутника. | |
| За властивістю дотичних, проведених з однієї точки, точки дотику вписаного кола до сторін трикутника відтинають від його сторін три пари рівних між собою відрізків: ВМ = ВN, NC = CР, AР = AM. | | Розташування центра кола, вписаного в рівнобедрений трикутник | Центр кола, вписаного в рівнобедрений трикутник, належить медіани, висоті і бісектрисі, що проведені з вершини до основи. | | Коло, вписане і описане навколо рівностороннього трикутника | Центри кола, описаного навколо рівностороннього трикутника, і кола, вписаного в нього, збігаються. Це точка перетину висот, медіан, бісектрис рівностороннього трикутника. | |
|
|
Радіус кола, вписаного в прямокутний трикутник | Радіус кола, вписаного в прямокутний трикутник, з катетами а і b та гіпотенузою с обчислюється за формулою  . . | | Вписане коло і трикутник | Коло, вписане в різносторонній трикутник | Коло, вписане в рівнобедрений трикутник | | | | Вписане коло і трикутник | Коло, вписане в рівносторонній трикутник | Коло, вписане в прямокутний трикутник | | | |
|







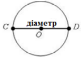
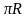 або C =
або C = 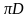

 R2
R2

 АО.
АО.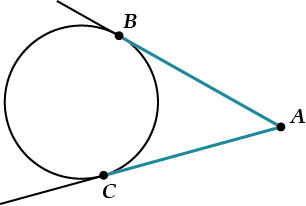
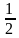 D
D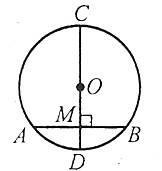
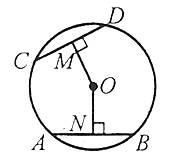
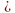 R1 + R2
R1 + R2