Координатный метод. Часть 2

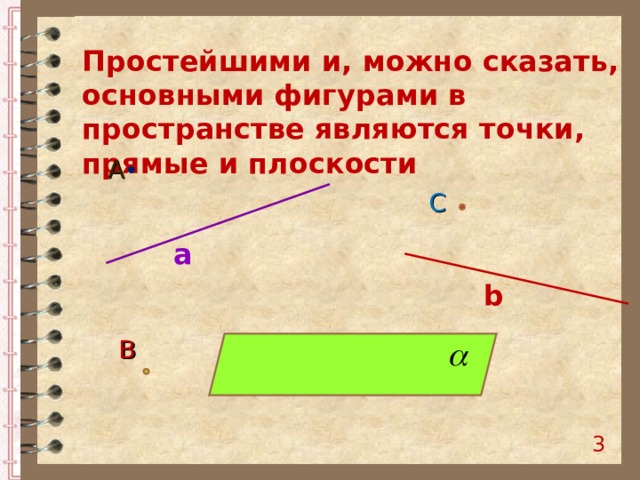
Простейшими и, можно сказать, основными фигурами в пространстве являются точки, прямые и плоскости

А

С

а

b

В

Прямоугольной системой координат в пространстве называется тройка взаимно перпендикулярных координатных прямых, имеющих общее начало – т.О(0;0;0)

z

O

y

х

4

Оси координат Ox, Oy , Oz

z

Ось аппликат

y

O

Ось ординат

х

Ось абсцисс

4

Вспомним способ построения точки по координатам: А(4;5;-3)

z

O

y

х

5

А(4;5;-3)

z

O

y

х

6

А(4;5;-3)

z

O

y

х

А(4;5;-3)

6

Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором

Конец вектора

В

АВ

Начало вектора

А

8

z

O

y

х

z

O

y

х

11

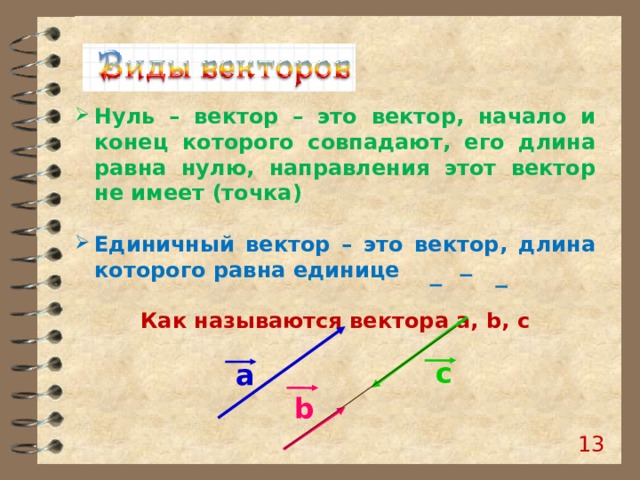
• Нуль – вектор – это вектор, начало и конец которого совпадают, его длина равна нулю, направления этот вектор не имеет (точка)

• Единичный вектор – это вектор, длина которого равна единице

Как называются вектора а, b, c

c

a

b

12

• Коллинеарные вектора – это вектора, лежащие на параллельных прямых или на одной прямой

• Сонаправленные вектора – это коллинеарные вектора, имеющие одинаковое направление

• Противоположнонаправленные вектора – это коллинеарные вектора, имеющие разное направление

13

Как называются вектора a, b, c ?

b

с

a

Как называются вектора i, j, k ?

13

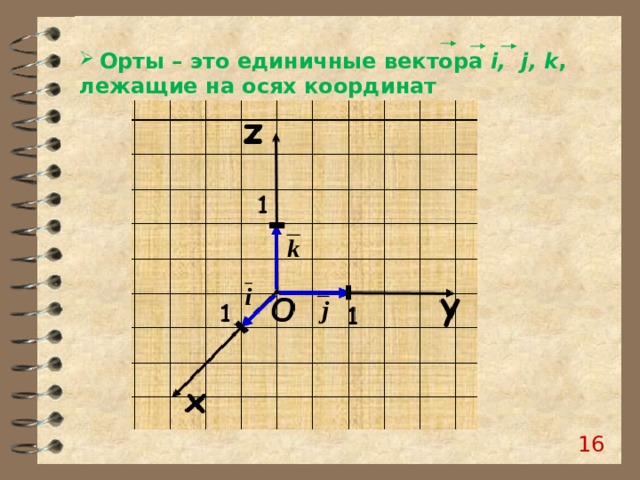
• Орты – это единичные вектора i, j, k ,

лежащие на осях координат

15

• Равные вектора – это сонаправленные вектора, имеющие равную длину

• Ортогональные вектора – это вектора, лежащие на перпендикулярных прямых

• Компланарные вектора – это вектора, лежащие в параллельных плоскостях

Если вектор задан своими координатами

, то

Например,

, тогда

В этом случае говорят, что вектор записан в ортах

• Умножение вектора на число.
• Сложение векторов.
• Вычитание векторов

18

• Умножение вектора на число.

a

a

a

18

a

b

2. Сложение векторов.

Правило треугольника.

b

b

a

a

20

a

b

2. Сложение векторов.

Правило параллелограмма.

b

b

a

a

b

a

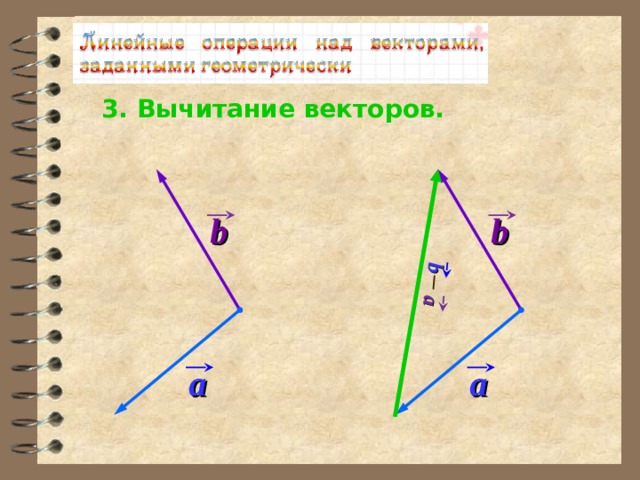
3. Вычитание векторов.

b

b

a

a

Пример 3

Пусть ABCD — параллелограмм, а O — произвольная точка пространства. Докажите, что

О

D

С

В

А

23

Решение

24

Пример 4

Дан прямоугольный параллелепипед KLMNK 1 L 1 M 1 N 1 . Докажите, что

24

Решение

M 1

N 1

K 1

L 1

N

M

K

L

24

M 1

N 1

L 1

K 1

N

M

K

L

27

M 1

N 1

Так как диагонали

MK 1 и M 1 K прямоугольного параллелепипеда равны, то

L 1

K 1

N

M

K

L

28

Пример 5

Дана треугольная призма ABCA 1 B 1 C 1 .

Укажите вектор x , начало и конец которого являются вершинами призмы, такой, что

29

Решение

30

Нужно найти вектор x , такой, что

Из этого равенства находим

30

Пример 6

Дан параллелепипед ABCDA 1 B 1 C 1 D 1 , Докажите, что:

B 1

C 1

D 1

A 1

B

C

А

D

32

Решение.

B 1

C 1

В прямоугольном параллелепипеде все диагонали равны, пересекаются в одной точке и этой точкой делятся пополам, следовательно

D 1

A 1

О

B

C

А

D

33

Пример 7

Точки E и F — середины рёбер AC и BD тетраэдра ABCD . Докажите, что

Компланарны ли векторы

Какие векторы называются компланарными?

34

Решение.

Найдем FE . Рассмотрим вектора FA и F С. Достроим на них параллелограмм CKAF .

Тогда, FK = FA + FC .

А FE – половина FK . Тогда

откуда

Найдем FA и FC

34

36

Какие вектора называются противоположно направленными?

Итак имеем

Перегруппируем слагаемые:

Точка F — середина отрезка BD, поэтому вектора FB и FD – противоположно направленные, а , значит,

Итак имеем

,

и

следовательно,

Что и требовалось доказать!

В задаче еще спрашивается, компланарны ли векторы

Мы доказали, что , т.е.

А это значит, что FE можно разложить через вектора BA и DC , что говорит об их компланарности.

Пример 8

Докажите, что если M — точка пересечения медиан треугольника ABC , а

т. O — произвольная

точка пространства,

то

40

Решение.

Найдем :

40

Итак,

Пример 9

Даны координаты четырёх вершин куба ABCDA 1 B 1 C 1 D 1 :

A (0; 0; 0), B (0; 0; 1), D (0; 1; 0), A 1 (1; 0; 0).

Найдите координаты остальных вершин куба.

Решение.

Изобразим на рисунке систему координат Axyz (с началом в точке A ) и отметим заданные точки B , D , A 1 (они лежат на осях координат). Через каждую из этих точек проведём плоскость, перпендикулярную той оси координат, на которой лежит эта точка. В результате получится куб ABCDA 1 B 1 C 1 D 1

Видно, что D 1 по оси A х имеет ту же координату,

что и А 1, по оси Ay – ту же, что и D , по оси А z – 0.

Аналогично, что С 1 по осям A х и Ay имеет те же

координаты, что и

а по оси А z – ту же координату, что и B(0; 0; 1).

Аналогично, что С по осям A х и Ay имеет те же

координаты, что и D(0; 1; 0),

а по оси А z – ту же координату, что и B(0; 0; 1).

Аналогично, что В 1 по осям A х и Ay имеет те же

координаты, что и A 1 (1; 0; 0),

а по оси А z – ту же координату, что и B(0; 0; 1).

Пример 9

На векторах ОА, ОВ, ОС построена пирамида. Найдите длину векторов ОМ – медиана основания, СК – медиана грани ОСВ и ВА, если A(0;8;0), B(2;7;-2), C (-1;2;7)

Решение.

A(0;8;0), B(2;7;- 1 ), C (-1;2;7)

z

C

Достроим пирамиду.

A

y

O

x

B

A(0;8;0), B(2;7;- 1 ), C (-1;2;7)

z

Найдем длину вектор ОМ – медиана основания.

Достроим треугольник ОАВ до параллелограмма ОАВК. Тогда

ОК=ОА+ОВ,

а ОК=2·ОМ

C

A

O

y

М

x

К

B

50

A(0;8;0), B(2;7;- 1 ), C (-1;2;7)

z

C

A

O

y

М

x

К

B

51

A(0;8;0), B(2;7;- 1 ), C (-1;2;7)

Найдем вектор СК – медиана грани ОСВ .

Достроим треугольник ОСВ до параллелограмма ОСВ D . Тогда

С D = CO + C В,

а CD =2· OK

D

52

Найдем вектор ВА:

Длины векторов находим по формуле: