Координатный метод. Часть 3

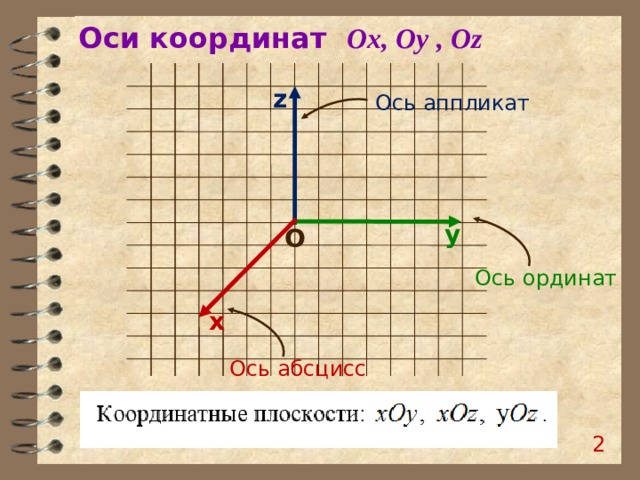
Оси координат Ox, Oy , Oz

z

Ось аппликат

y

O

Ось ординат

х

Ось абсцисс

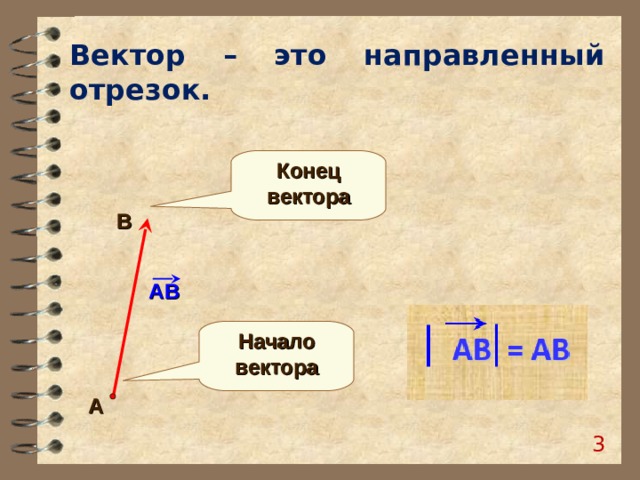
Вектор – это направленный отрезок.

Конец вектора

В

АВ

Начало вектора

А

2

Вектор может быть задан длиной и направлением – геометрически.

Вектор может быть задан своими координатами – аналитически.

Вектор может быть задан координатами начала и конца – аналитически.

Самостоятельно постройте вектор

АВ(-5;-3;-7)

3 минуты

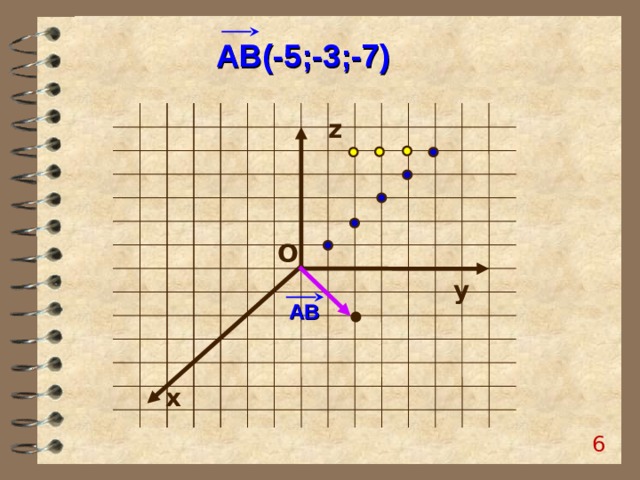
АВ(-5;-3;-7)

z

O

y

АВ

х

5

• Коллинеарные вектора – это вектора, лежащие на параллельных прямых или на одной прямой

• Сонаправленные вектора – это коллинеарные вектора, имеющие одинаковое направление

• Противоположнонаправленные вектора – это коллинеарные вектора, имеющие разное направление

6

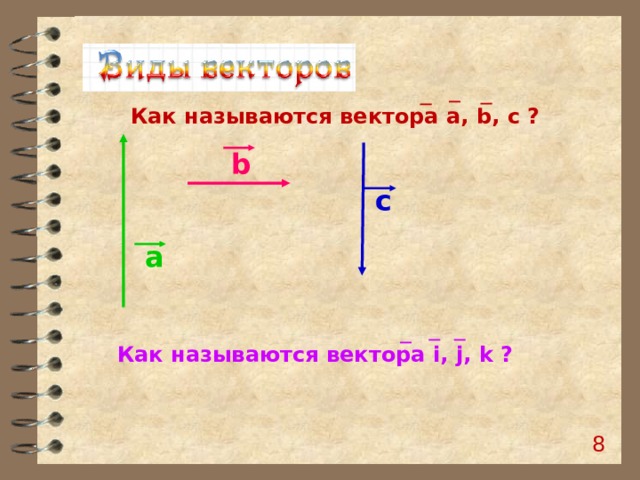
Как называются вектора a, b, c ?

b

с

a

Как называются вектора i, j, k ?

6

• Равные вектора – это сонаправленные вектора, имеющие равную длину

• Ортогональные вектора – это вектора, лежащие на перпендикулярных прямых

• Компланарные вектора – это вектора, лежащие в параллельных плоскостях

8

Если вектор задан своими координатами

, то

В этом случае говорят, что вектор записан в ортах, и его длину можно вычислить по формуле:

8

• Умножение вектора на число.
• Сложение векторов.
• Вычитание векторов

10

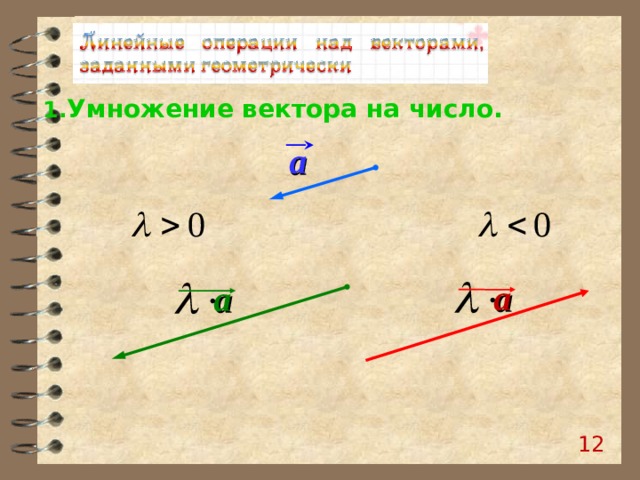
• Умножение вектора на число.

a

a

a

10

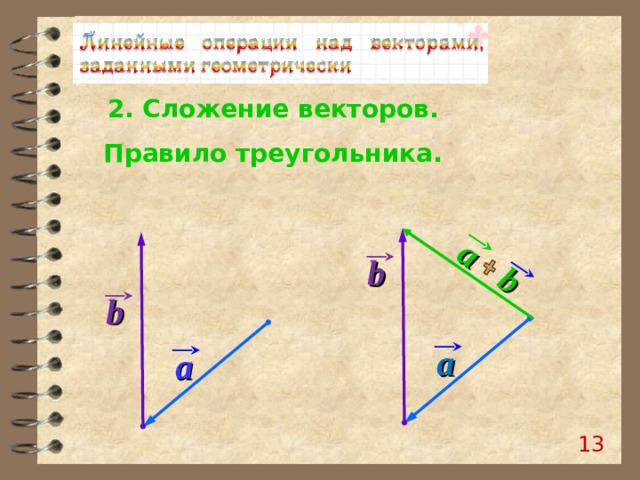
a

b

2. Сложение векторов.

Правило треугольника.

b

b

a

a

12

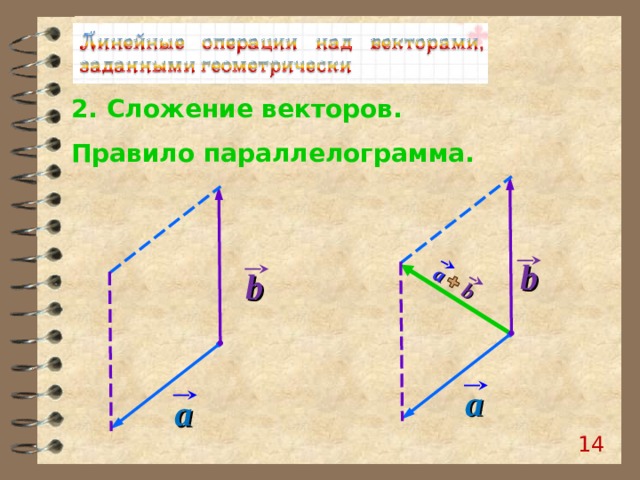
a

b

2. Сложение векторов.

Правило параллелограмма.

b

b

a

a

14

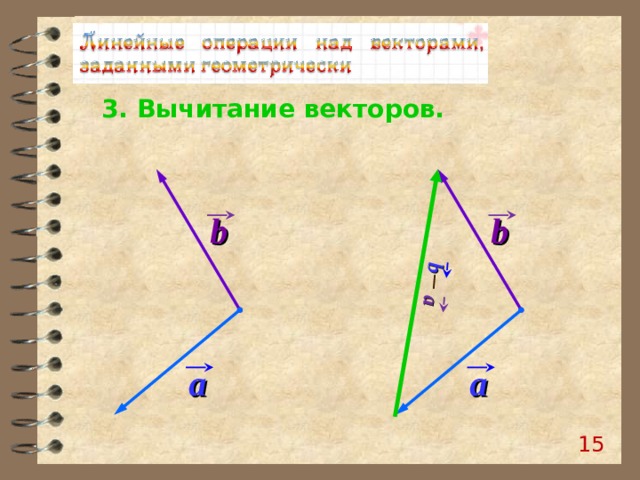
b

a

3. Вычитание векторов.

b

b

a

a

15

O

Вершина пирамиды

Многоугольник - основание

В

А

С

E

15

D

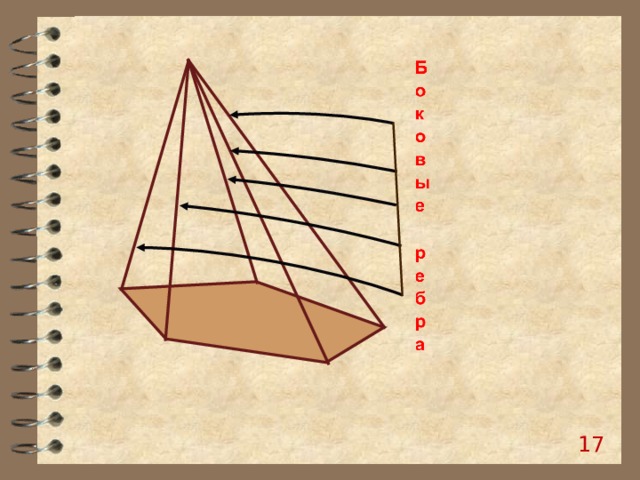
16

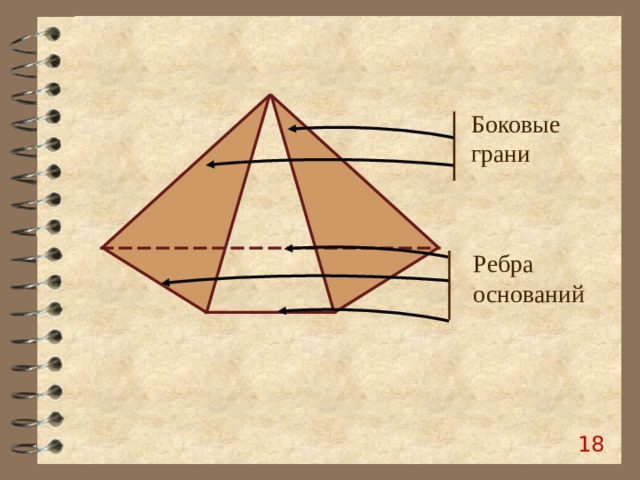
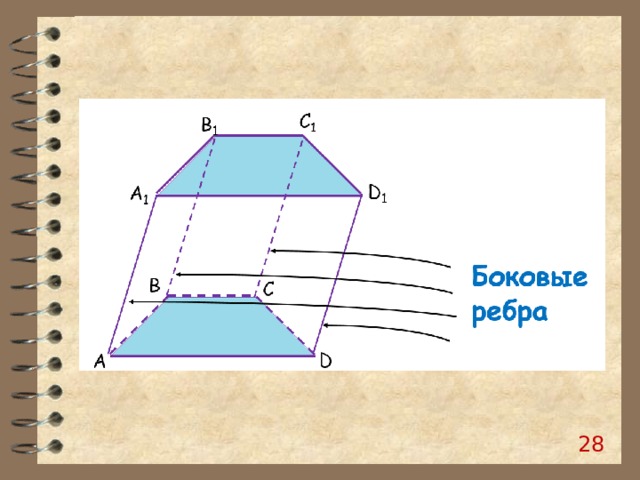
Боковые грани

Ребра оснований

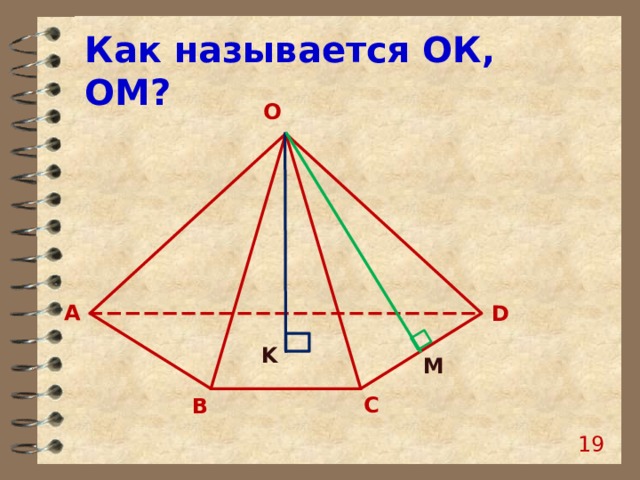
Как называется ОК, ОМ?

O

A

D

K

M

C

B

18

Какая пирамида называется правильной?

19

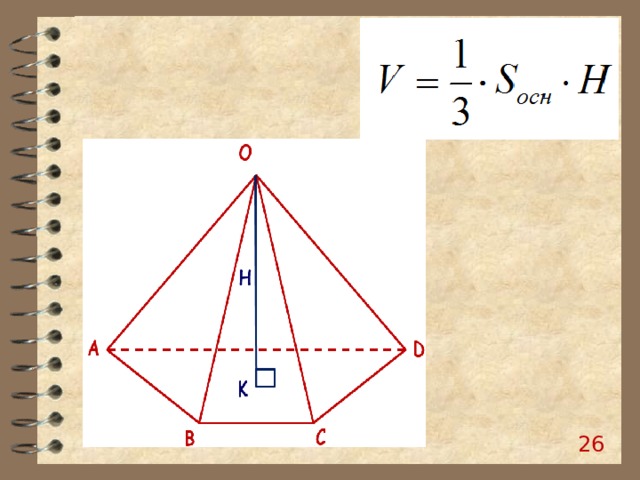
Пирамида называется правильной, если ее основание — правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания (ОК), является ее высотой.

19

Если пирамида – правильная, то КЕ - ?

19

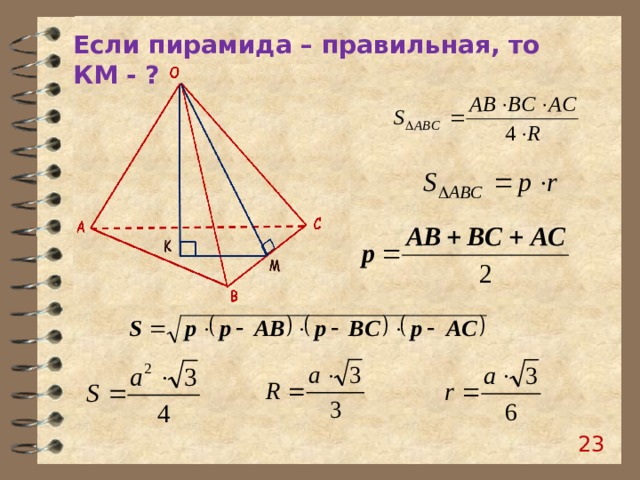
Если пирамида – правильная, то КМ - ?

19

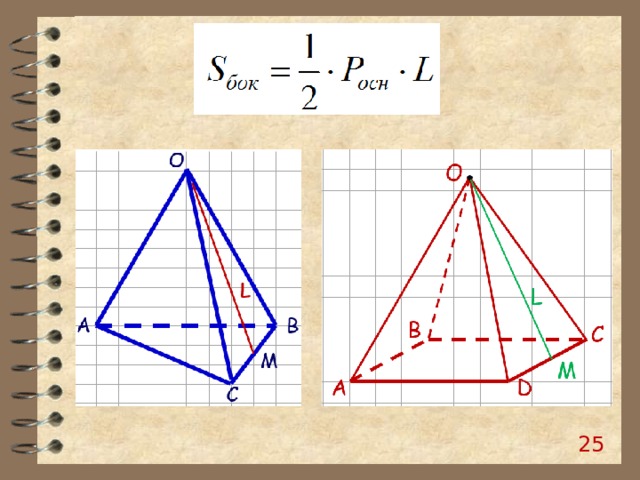
Площадь полной поверхности пирамиды — сумма площадей ВСЕХ ее граней, т.е.

19

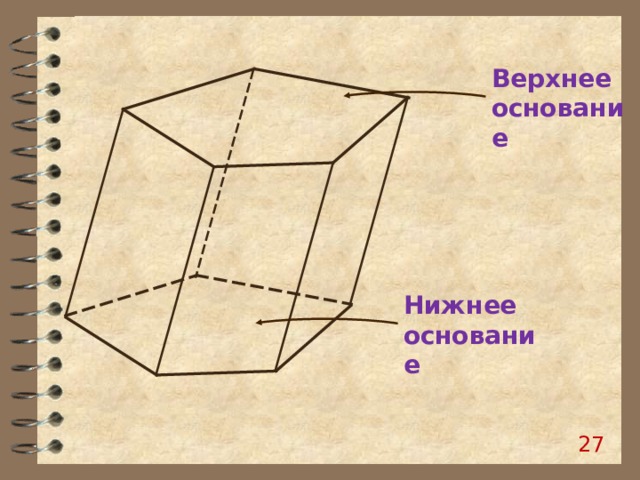
Верхнее основание

Нижнее основание

27

27

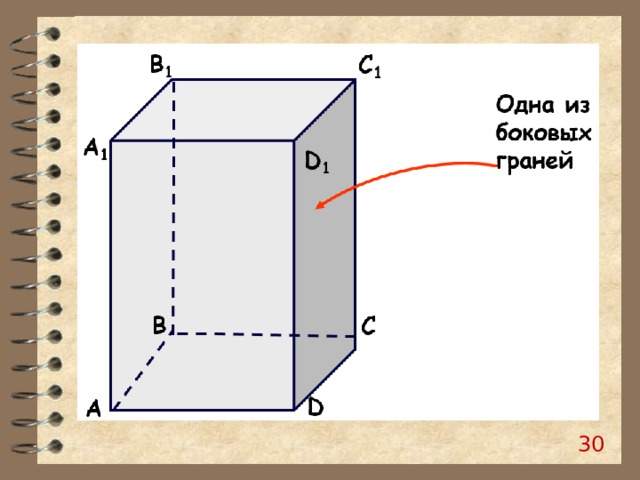
27

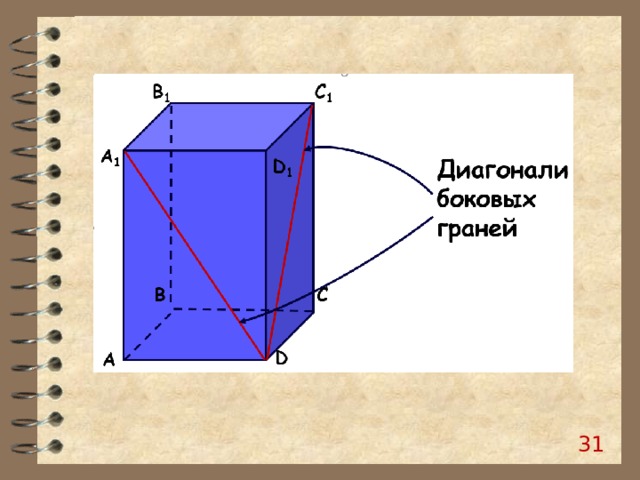
27

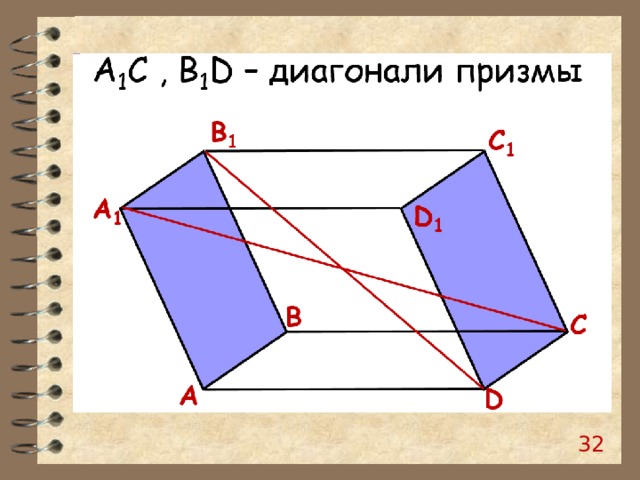
27

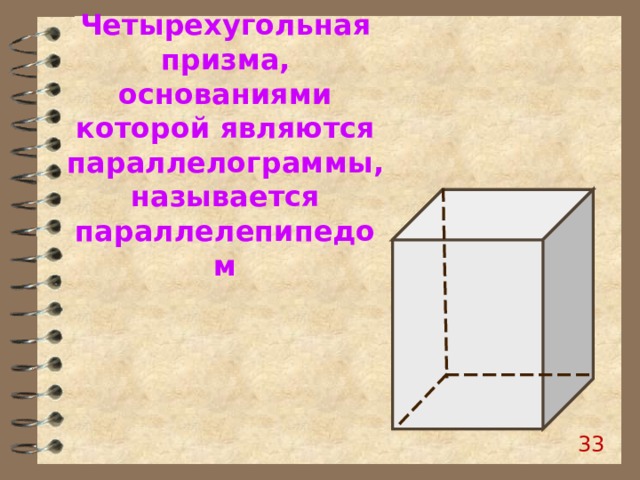
Четырехугольная призма, основаниями которой являются параллелограммы, называется параллелепипедом

27

Если все боковые ребра призмы перпендикулярны к плоскостям ее оснований, то призма называется прямой

Правильная четырехугольная призма КУБ

Все грани куба – одинаковые квадраты

33

Площадь полной поверхности призмы равна сумме площади боковой поверхности и площадей оснований.

Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы, т. е. на длину бокового ребра

33

Объем прямой призмы равен произведению площади основания на боковое ребро призмы.

35

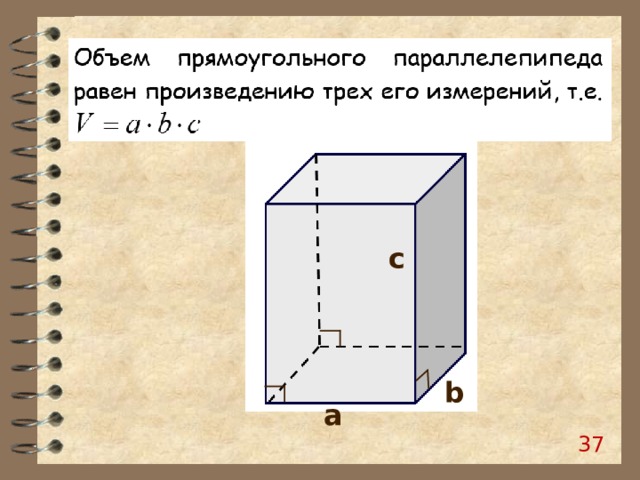
c

b

а

35

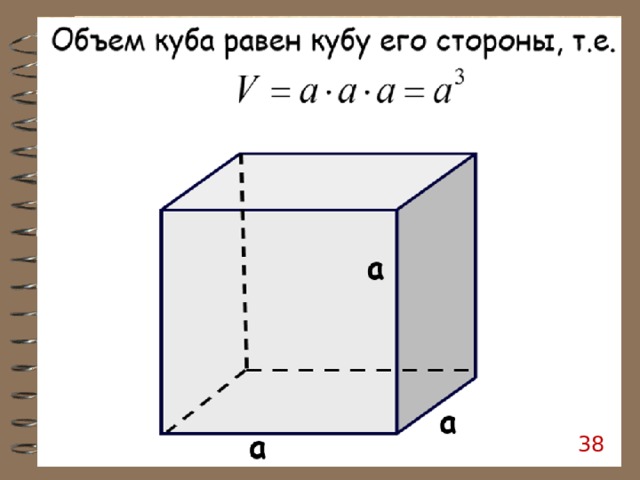
37

Пример 10

Дана пирамида с вершиной в точке D ( 1 ; 10 ; 8 ), основание которой – треугольник, построенный на векторах АВ и АС. Ребро AD перпендикулярно основанию АВС. Найдите площадь боковой поверхности и объем пирамиды, если А( 1;2;0), B(3;-2;4), C(3;6;-4)

37

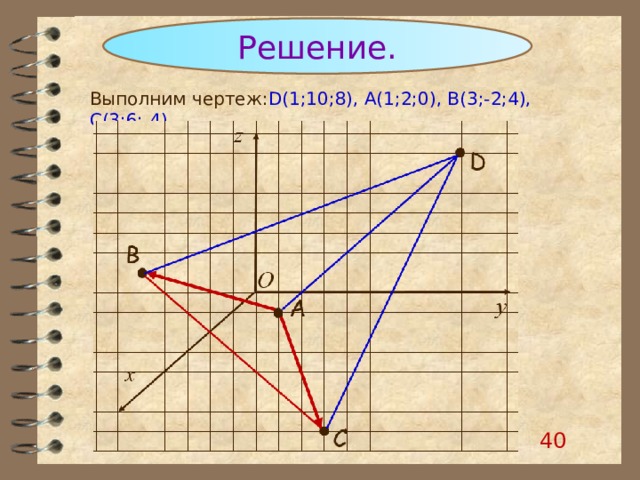
Решение.

Выполним чертеж: D ( 1 ; 10 ; 8 ) , А( 1;2;0), B(3;-2;4), C(3;6;-4)

37

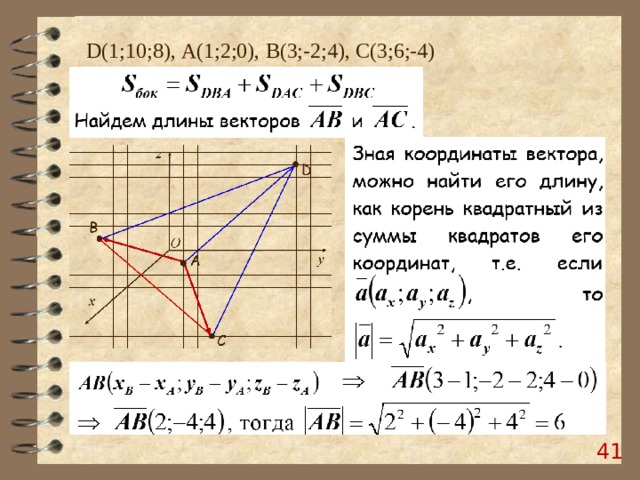
D (1;10;8), А(1;2;0), B (3;-2;4), C (3;6;-4)

37

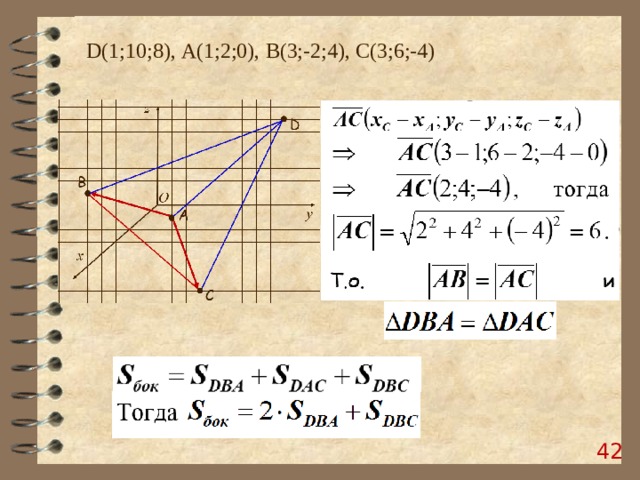
D (1;10;8), А(1;2;0), B (3;-2;4), C (3;6;-4)

37

D (1;10;8), А(1;2;0), B (3;-2;4), C (3;6;-4)

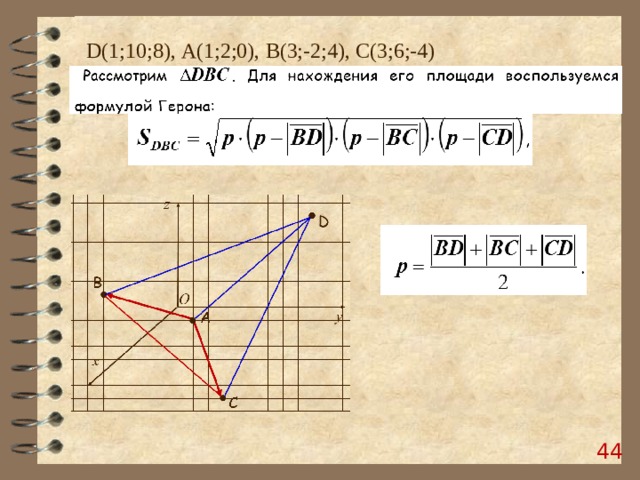
D (1;10;8), А(1;2;0), B (3;-2;4), C (3;6;-4)

D (1;10;8), А(1;2;0), B (3;-2;4), C (3;6;-4)

D (1;10;8), А(1;2;0), B (3;-2;4), C (3;6;-4)

D (1;10;8), А(1;2;0), B (3;-2;4), C (3;6;-4)

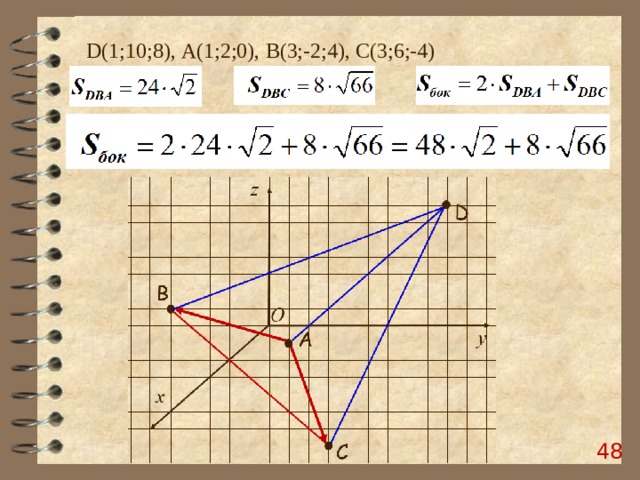
D (1;10;8), А(1;2;0), B (3;-2;4), C (3;6;-4)

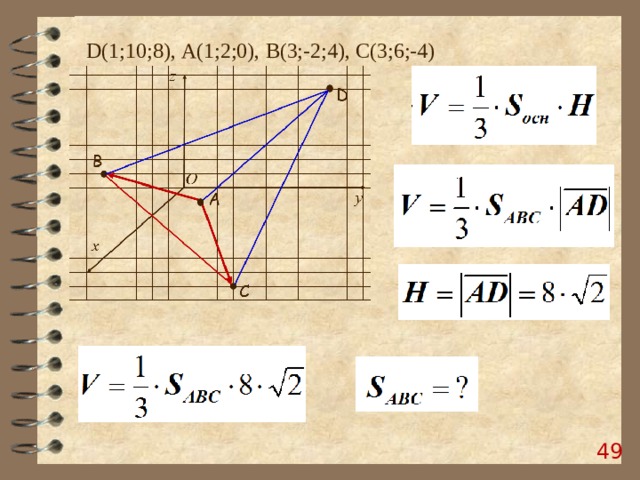
D (1;10;8), А(1;2;0), B (3;-2;4), C (3;6;-4)

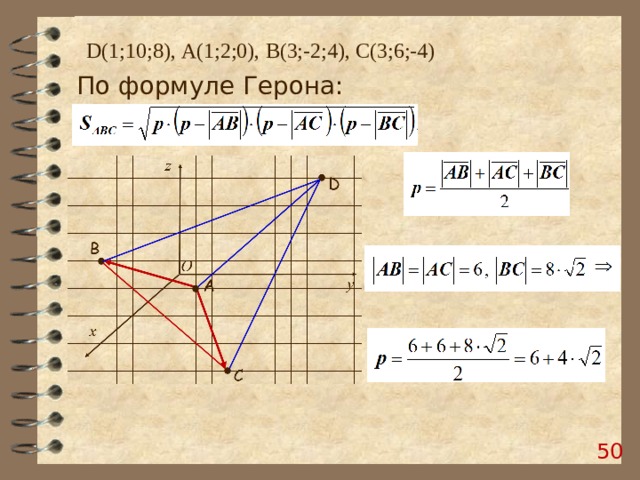
D (1;10;8), А(1;2;0), B (3;-2;4), C (3;6;-4)

По формуле Герона:

D (1;10;8), А(1;2;0), B (3;-2;4), C (3;6;-4)

По формуле Герона:

Пример 1 1

Точки М(7; 7; 11), А(0; 8; 1), В(6; 0; 1) и 0(14; 6; 1) являются вершинами правильной четырехугольной пирамиды MABCD. Найдите высоту и площадь боковой поверхности пирамиды.

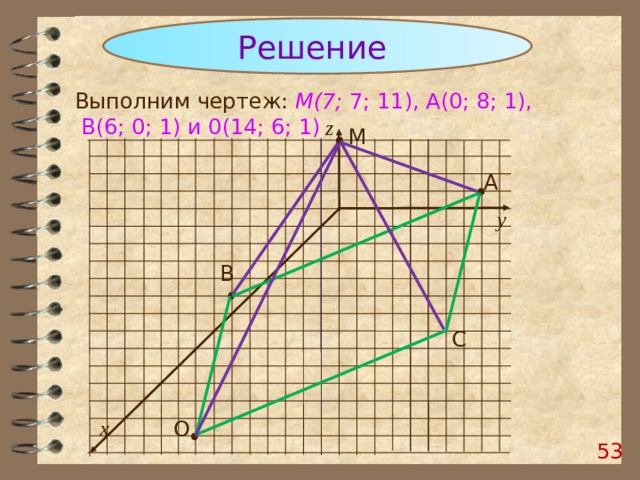
Решение

Выполним чертеж: М(7; 7; 11), А(0; 8; 1), В(6; 0; 1) и 0(14; 6; 1)

z

М

А

y

В

С

x

О

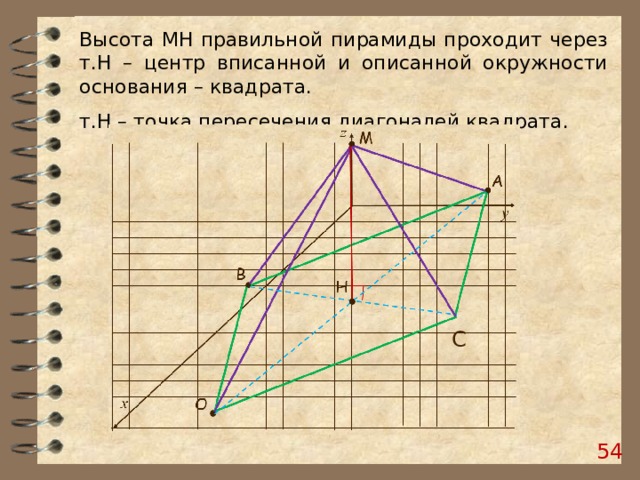
Высота МН правильной пирамиды проходит через т.Н – центр вписанной и описанной окружности основания – квадрата.

т.Н – точка пересечения диагоналей квадрата.

С

53

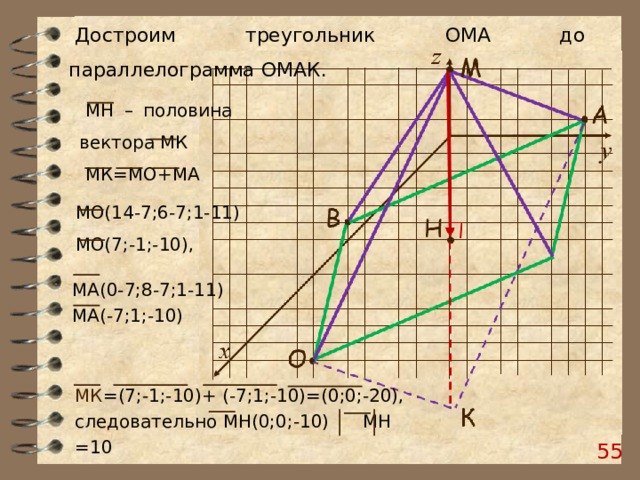
Достроим треугольник ОМА до параллелограмма ОМАК.

МН – половина вектора МК

МК=МО+МА

МО(14-7;6-7;1-11)

МО(7;-1;-10),

МА(0-7;8-7;1-11)

МА(-7;1;-10)

МК =(7;-1;-10)+ (-7;1;-10)=(0;0;-20), следовательно МН(0;0;-10) МН =10

54

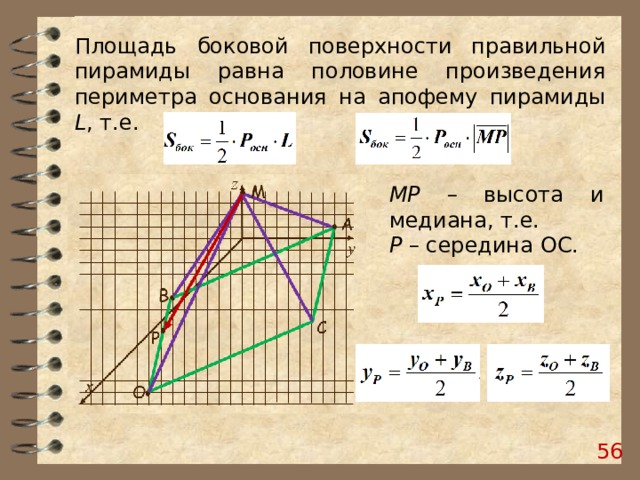
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему пирамиды L , т.е.

МР – высота и медиана, т.е.

Р – середина O С.

55

М(7; 7; 11), А(0; 8; 1), В(6; 0; 1) и 0(14; 6; 1)

МР(10-7;3-7;1-11) или МР(3;-4;-10)

57

М(7; 7; 11), А(0; 8; 1), В(6; 0; 1) и 0(14; 6; 1)

Найдем периметр основания пирамиды – квадрата – все стороны равны:

АВ(6-0;0-8;1-1) или АВ(6;-8;0)

Значит периметр основания пирамиды

Р осн. =4·10=40 .

58

Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними

Скалярное произведение векторов

а и b принято обозначать или точкой a·b , или круглыми скобками (a b)

1. Скалярное произведение обладает переместительным свойством, то есть

2. Скалярное произведение обладает распределительным свойством, то есть

3. Скалярное произведение обладает сочетательным свойством относительно

числового множителя, то есть

4. Скалярное произведение вектора самого на себя называется скалярным квадратом вектора. Скалярный квадрат вектора равен квадрату его модуля. То есть

5. Скалярное произведение одноименных ортов равно единице

6. Скалярное произведение разноименных ортов равно нулю.

7. Скалярное произведение векторов, заданных своими координатами:

8. Угол между двумя векторами:

9. Если , то

.

10. Проекция вектора а на вектор b

Если вектора заданы своими координатами, т.е.

то

и

.

Пример 12

66

Решение

2) Проверим, являются ли вектора а и b ортогональными. По свойствам скалярного произведения :

3) Найдем проекцию вектора p на вектор q

По свойствам скалярного произведения проекцию вектора p на вектор q можно найти по формуле:

Пример 13

Даны векторы a (3;-6;1) и b (1;5;4). Требуется:

72

Решение

a (3;-6;1), b (1;5;4)

1) По свойствам скалярного произведения если

и , то

тогда

73

a (3;-6;1), b (1;5;4).

Вычислим

1

Найдем координаты векторов и

74

Итак a (3;-6;1), b (1;5;4), ,

75

a (3;-6;1), b (1;5;4). Найдем длину вектора

2

.

По формулам скалярного произведения

Найдем координаты вектора q :

;

Т.о. q(6;9;13) , тогда

75

a (3;-6;1), b (1;5;4). Проверим, ортогональны ли вектора и

3

Найдем координаты векторов p и q

Итак p (10;8;18) и q (1;-37;-18)

77

a (3;-6;1), b (1;5;4). Проверим, ортогональны ли вектора p (10;8;18) и q (1;-37;-18)

3

Найдем скалярное произведение векторов

p (10;8;18) и q (1;-37;-18)

78

a (3;-6;1), b (1;5;4). Найдем проекцию вектора p (10;8;18) на вектор q (1;-37;-18) . По свойствам скалярного произведения:

4

Скалярное произведение p · q было вычислено ранее, поэтому нам осталось вычислить q

Таким образом

79

80

80