| КС109 | ОП.01 Основы теории информации |
| Преподаватель: Класс Юлия Николаевна |
| E-mail: [email protected] |
| Дата выдачи задания | Срок выполнения |
| 10.11.2020г. | 11.11.2020г. |
|
|
|
| ТЕМА ЗАНЯТИЯ: | ОЦЕНКА КОЛИЧЕСТВА ИНФОРМАЦИИ |
| Список литературы:
| Лекция (Код доступа: https://cloud.mail.ru/public/4yHZ/2Wx8n82W9 |
Задание: Рассмотреть решение задач по образцу, выполнить задания
Типовой пример. По двоичному симметричному каналу связи с помехами передаются два сигнала x1 и x2 с априорными вероятностями P(x1)=3/4 и P(x2)=1/4. Из-за наличия помех вероятность правильного приема каждого из сигналов уменьшается до 7/8. Требуется определить:
1) полную информацию I(X) на выходе источника сигналов;
2) взаимную частную информацию I(y2,x2) двух случайных сигналов на выходе и входе канала связи относительно друг друга (т.е. количество информации о сигнале x2 источника в сообщении y2 приемника);
3) условную частную информацию I(x2/y2), содержащуюся в сообщении x2 источника при условии приема сообщения y2;
4) среднее количество информации I(y2,X) в принятом сообщении y2 относительно всех передаваемых сообщений X(x1,x2);
5) среднее количество взаимной информации I(Y,X) в сообщениях Y приемника о сообщениях X источника;
Решение. По условию:
а) безусловные вероятности P(xi)=Pxi сообщений x1 и x2:
 ;
;  .
.
б) условные вероятности P(yj/xi)= приема сообщений y1, y2 при условии передачи сообщений x1, x2:
приема сообщений y1, y2 при условии передачи сообщений x1, x2:
 ;
;  ;
;  ;
;  .
.
Вычислим вероятности P(yj)=Pyj , P(xi, yj)=Pxyi,j и P(xi/yj)=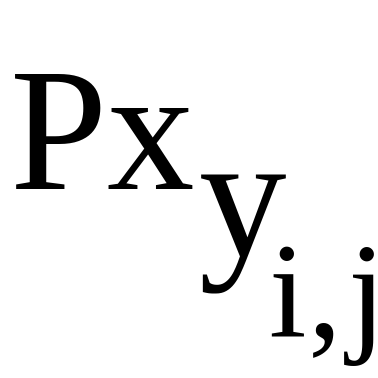 при
при  и
и  , необходимые для расчета информационных характеристик:
, необходимые для расчета информационных характеристик:

.
;
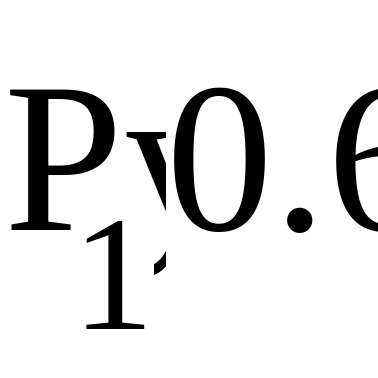
;

 задание начального значения индексов;
задание начального значения индексов;
 ;
;  .
.
Итак,  ;
;  ;
;
 ;
;  .
.
Так как  или
или  ,
,
то имеем следующие условные вероятности

.
, т.е.
 ;
;  ; ;
; ;
Определим единицы измерения количества информации:
а) при натуральном логарифме (нит) ;
б) при двоичном логарифме (бит) .
В случае дискретного источника полное количество информации на его выходе в расчете на одно сообщение, согласно (2.2), совпадает с энтропией источника (1.1) и будет
; или .
Согласно (2.7), взаимная частная информация I(y2,x2) двух сигналов
или ;
; .
Условная частная информация I(x2/y2)
; .
Согласно (2.5), среднее количество информации I(yj,X) в принятом сообщении yj относительно всех передаваемых сообщений X
; ;
; .
Согласно (2.4), среднее количество взаимной информации I(Y,X) в сообщениях Y приемника относительно всех передаваемых сообщений X
; .
Рассмотрим второй способ определения I(Y,X). Найдем, согласно (1.5), условную энтропию источника при условии снятия неопределенности приемника
; .
Тогда на основании (2.3) с учетом I(X)=H(X) среднее количество взаимной информации I(Y,X) в расчете на одно сообщение
; .
Типовые задачи.
Задача 1. В линию связи посылаются равновероятные и статистически независимые дискретные сигналы x1 и x2 ( ). Действие помех приводит к тому, что на выходе канала связи имеются сигналы z1, z2 и z3 ( ) с матрицей условных вероятностей P(zi/xj)= при
). Действие помех приводит к тому, что на выходе канала связи имеются сигналы z1, z2 и z3 ( ) с матрицей условных вероятностей P(zi/xj)= при 
.
, например,
Определить полную взаимную информацию I(X,Z)=IXZ.
Ответ. Матрица безусловных вероятностей выходного сигнала
.
Матрица совместных вероятностей входного и выходного сигналов
.
Полная взаимная информация .
Задача 2. Измеряемая величина X на интервале [ ] при с параметрами и
имеет усеченный нормальный закон распределения с плотностью вероятности (рис.2.3.1 при и )
.
Погрешность каждого результата измерения (например, ) при параметре имеет распределение Лапласа (двустороннее экспоненциальное) с плотностью вероятности (рис.2.3.1 при и )
.
Рис.2.3.1
Требуется найти количество информации, получаемой в среднем на одно измерение.
Ответ. Коэффициент
.
Количество информации
,  .
.
Задача 3. Информация передается путем изменения амплитуды сигнала x, распределенной по нормальному закону с параметрами среднее значение и дисперсия . Величина X измеряется регистрирующим устройством с погрешностью Z, не зависящей от амплитуды сигнала и также распределенной по нормальному закону со средним значением и дисперсией .
Определить количество информации I(X,Y)=IXY о величине X, содержащееся в результатах измерения Y=X+Z.
Ответ. ______________________________________________________________________
Задача 4. По каналу связи с одинаковыми вероятностями передаются статистически независимых сигнала xi ( ). При отсутствии помех передаваемому сигналу xj соответствует на выходе канала сигнал yj ( ). При наличии помех каждый передаваемый сигнал может быть с вероятностью принят правильно и с вероятностью искажен и перейти при этом в любой из остальных выходных сигналов.
Определить среднее количество информации на один сигнал, передаваемое по каналу при наличии и отсутствии помех.
Ответ. ___________________________________________________________
Задача 5. Система передачи информации характеризуется при , и  матрицей P(X,Y)=Pxy совместных вероятностей
матрицей P(X,Y)=Pxy совместных вероятностей
.
Определить среднее количество взаимной информации I(X,Y)=IXY.
Ответ. ___________________________________________________________________________








 или
или 









